2014高一数学（人教A版）必修2能力强化提升：3-2-1 直线的点斜式方程

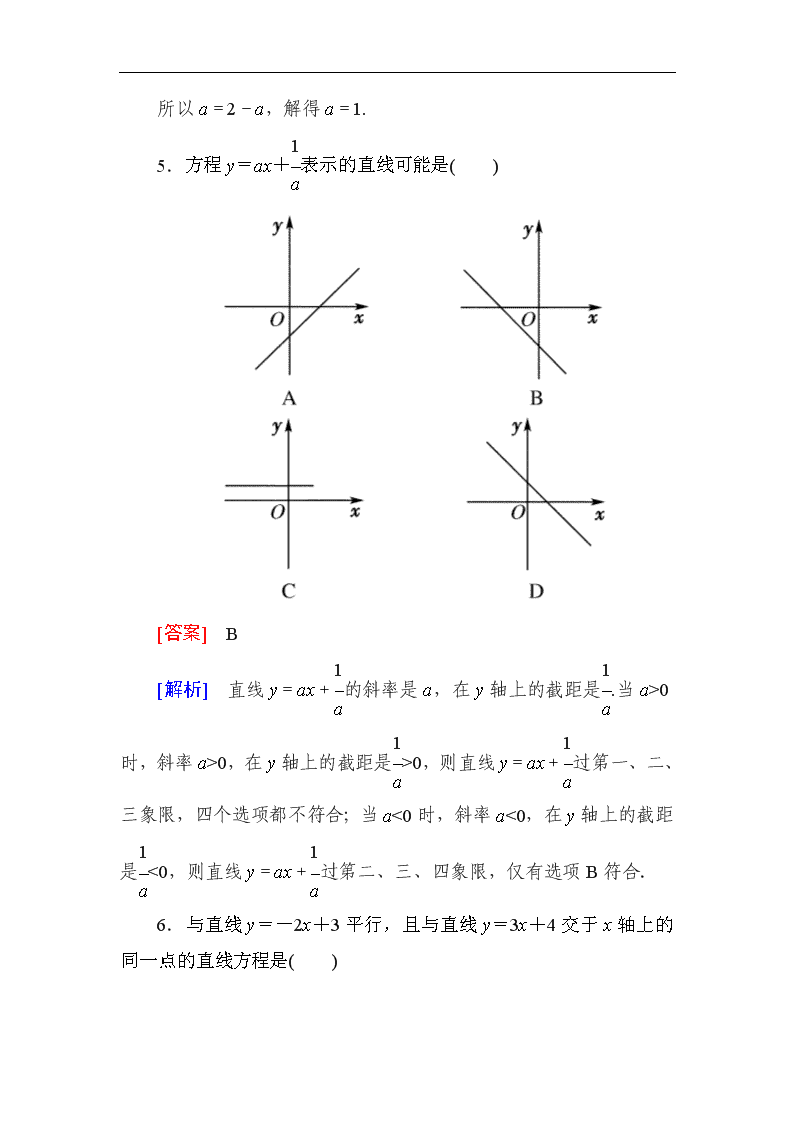
2014高一数学（人教A版）必修2能力强化提升：3-2-1 直线的点斜式方程

一、选择题 ‎1．直线y＝－2x＋3的斜率和在y轴上的截距分别是(　　)‎ A．－2,3 B．3，－2‎ C．－2，－2 D．3,3‎ ‎[答案]　A ‎2．过点(1,3)且斜率不存在的直线方程为(　　)‎ A．x＝1 B．x＝3‎ C．y＝1 D．y＝3‎ ‎[答案]　A ‎3．方程y－y0＝k(x－x0)(　　)‎ A．可以表示任何直线 B．不能表示过原点的直线 C．不能表示与y轴垂直的直线 D．不能表示与x轴垂直的直线 ‎[答案]　D ‎[解析]　直线的点斜式方程不能表示没有斜率的直线，即不能表示与x轴垂直的直线．‎ ‎4．已知两条直线y＝ax－2和y＝(2－a)x＋1互相平行，则a等于(　　)‎ A．2 B．1‎ C．0 D．－1‎ ‎[答案]　B ‎[解析]　根据两条直线的方程可以看出它们的斜率分别是k1＝a，k2＝2－a.两直线平行，则有k1＝k2.‎ 所以a＝2－a，解得a＝1.‎ ‎5．方程y＝ax＋表示的直线可能是(　　)‎ ‎[答案]　B ‎[解析]　直线y＝ax＋的斜率是a，在y轴上的截距是.当a>0时，斜率a>0，在y轴上的截距是>0，则直线y＝ax＋过第一、二、三象限，四个选项都不符合；当a<0时，斜率a<0，在y轴上的截距是<0，则直线y＝ax＋过第二、三、四象限，仅有选项B符合．‎ ‎6．与直线y＝－2x＋3平行，且与直线y＝3x＋4交于x轴上的同一点的直线方程是(　　)‎ A．y＝－2x＋4 B．y＝x＋4‎ C．y＝－2x－ D．y＝x－ ‎[答案]　C ‎[解析]　y＝3x＋4与x轴交点为(－，0)，‎ 又与直线y＝－2x＋3平行，‎ 故所求直线方程为y＝－2(x＋)‎ 即y＝－2x－　故选C.‎ ‎7．直线l：y－1＝k(x＋2)的倾斜角为135°，则直线l在y轴上的截距是(　　)‎ A．1 B．－1‎ C. D．－2‎ ‎[答案]　B ‎[解析]　∵倾斜角为135°，‎ ‎∴k＝tan135°＝－tan45°＝－1，‎ ‎∴直线l：y－1＝－(x＋2)，令x＝0得y＝－1.‎ ‎8．等边△PQR中，P(0,0)、Q(4,0)，且R在第四象限内，则PR和QR所在直线的方程分别为(　　)‎ A．y＝±x B．y＝±(x－4)‎ C．y＝x和y＝－(x－4)‎ D．y＝－x和y＝(x－4)‎ ‎[答案]　D ‎[解析]　直线PR，RQ的倾斜角分别为120°，60°，‎ ‎∴斜率分别为－，.数形结合得出．‎ 二、填空题 ‎9．过点(－1,3)，且斜率为－2的直线的斜截式方程为________．‎ ‎[答案]　y＝－2x＋1‎ ‎[解析]　点斜式为y－3＝－2(x＋1)，化为斜截式为y＝－2x＋1.‎ ‎10．已知直线l1过点P(2,1)且与直线l2：y＝x＋1垂直，则l1的点斜式方程为________．‎ ‎[答案]　y－1＝－(x－2)‎ ‎[解析]　设l1的斜率为k1，l2的斜率为k2，‎ ‎∵l1⊥l2，∴k1k2＝－1.‎ 又k2＝1，∴k1＝－1.‎ ‎∴l1的点斜式方程为y－1＝－(x－2)．‎ ‎11．已知点(1，－4)和(－1,0)是直线y＝kx＋b上的两点，则k＝________，b＝________.‎ ‎[答案]　－2　－2‎ ‎[解析]　由题意，得解得k＝－2，b＝－2.‎ ‎12．△ABC的顶点A(5，－1)，B(1,1)，C(2，m)，若△ABC为直角三角形，则直线BC的方程为________．‎ ‎[答案]　8x＋y－9＝0或2x－y－1＝0或y＝x或3x＋y－4＝0‎ ‎[解析]　若∠A为直角，则AC⊥AB，‎ ‎∴kAC·kAB＝－1，‎ 即·＝－1，得m＝－7；‎ 此时BC：8x＋y－9＝0.‎ 若∠B为直角，则AB⊥BC，∴kAB·kBC＝－1，‎ 即－·＝－1，得m＝3；‎ 此时直线BC方程为2x－y－1＝0.‎ 若∠C为直角，则AC⊥BC，∴kAC·kBC＝－1，‎ 即·＝－1，得m＝±2.‎ 此时直线BC方程为y＝x或3x＋y－4＝0.‎ 三、解答题 ‎13．已知直线l1的方程为y＝－2x＋3，l2的方程为y＝4x－2，直线l与l1平行且与l2在y轴上的截距相同，求直线l的方程．‎ ‎[解析]　由斜截式方程知直线l1的斜率k1＝－2.‎ 又∵l∥l1，∴l的斜率k＝k1＝－2.‎ 由题意知l2在y轴上的截距为－2，‎ ‎∴l在y轴上的截距b＝－2，‎ ‎∴由斜截式可得直线l的方程为y＝－2x－2.‎ ‎14．已知△ABC的三个顶点分别是A(－5,0)，B(3，－3)，C(0,2)，试求BC边上的高所在直线的点斜式方程．‎ ‎[分析]　BC边上的高与边BC垂直，由此求得BC边上的高所在直线的斜率，从而由点斜式得直线方程．‎ ‎[解析]　设BC边上的高为AD，则BC⊥AD，‎ ‎∴kBCkAD＝－1.‎ ‎∴kAD＝－1，解得kAD＝.‎ ‎∴BC边上的高所在直线的点斜式方程是y－0＝(x＋5)．‎ 即y＝x＋3.‎ ‎15．已知直线y＝－x＋5的倾斜角是直线l的倾斜角的大小的5倍，分别求满足下列条件的直线l的方程．‎ ‎(1)过点P(3，－4)；‎ ‎(2)在x轴上截距为－2；‎ ‎(3)在y轴上截距为3.‎ ‎[解析]　直线y＝－x＋5的斜率k＝tanα＝－，∴α＝150°，‎ 故所求直线l的倾斜角为30°，斜率k′＝.‎ ‎(1)过点P(3，－4)，由点斜式方程得：‎ y＋4＝(x－3)，‎ ‎∴y＝x－－4.‎ ‎(2)在x轴截距为－2，即直线l过点(－2,0)，‎ 由点斜式方程得：y－0＝(x＋2)，∴y＝x＋.‎ ‎(3)在y轴上截距为3，由斜截式方程得y＝x＋3.‎ ‎16．求与两坐标轴围成面积是12，且斜率为－的直线方程．‎ ‎[解析]　设直线方程为y＝－x＋b，‎ 令y＝0得x＝b，‎ 由题意知·|b|·|b|＝12，∴b2＝36，‎ ‎∴b＝±6，∴所求直线方程为y＝－x±6.‎