- 2021-06-30 发布 |
- 37.5 KB |
- 44页


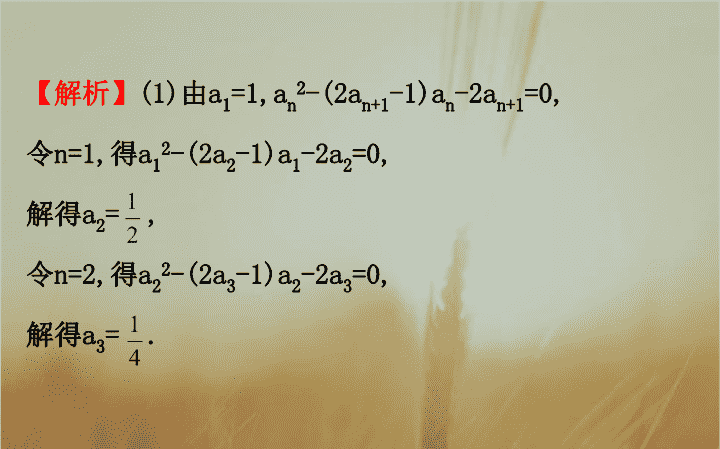
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019届二轮复习数列课件(44张)(全国通用)
渭源县第二中学 何华 数列 类型一 : 等差、等比数列的基本运算 【 典例 1】 (2016 · 全国卷 Ⅲ) 已知各项都为正数的数列 {a n } 满足 a 1 =1, a n 2 -(2a n+1 -1)a n -2a n+1 =0. (1) 求 a 2 ,a 3 . (2) 求 {a n } 的通项公式 . 【 解析 】 (1) 由 a 1 =1,a n 2 -(2a n+1 -1)a n -2a n+1 =0, 令 n=1, 得 a 1 2 -(2a 2 -1)a 1 -2a 2 =0, 解得 a 2 = , 令 n=2, 得 a 2 2 -(2a 3 -1)a 2 -2a 3 =0, 解得 a 3 = . (2) 由 a n 2 -(2a n+1 -1)a n -2a n+1 =0 得 2a n+1 (a n +1)=a n (a n +1). 因为 {a n } 的各项都为正数 , 所以 故 {a n } 是首项为 1, 公比为 的等比数列 , 因此 a n = . 【 规律总结 】 等差、等比数列基本量的计算方法 在等差 ( 等比 ) 数列的通项公式和前 n 项和公式中含有五个基本量 , 即 a 1 ,d(q),a n ,n,S n . 知道其中的三个 , 可以通过列方程 ( 组 ) 求其余两个 , 即 “ 知三求二 ” . 在解决等差 ( 等比 ) 数列问题中 , 往往是化为基本量的运算 , 有时也可灵活使用等差 ( 等比 ) 数列的性质解题 . 【 巩固训练 】 等比数列 {a n } 的前 n 项和为 S n , 公比 q>0, 已知 S 3 =14,S 6 =126. (1) 求数列 {a n } 的通项公式 . (2) 若 a 3 ,a 5 分别为等差数列 {b n } 的第 4 项和第 16 项 , 试求数列 {b n } 的通项公式及前 n 项和 T n . 【 解题指南 】 (1) 由 S 3 =14,S 6 =126 建立关于 a 1 ,q 的方程组求出 a 1 ,q, 再求 a n . (2) 由 b 4 ,b 16 求 b 1 和 d, 再由通项公式及前 n 项和公式求解 . 【 解析 】 (1) 易知 q≠1, 由已知得 解得 a 1 =q=2. 所以 a n =2 n . (2) 由 (1) 得 a 3 =8,a 5 =32, 则 b 4 =8,b 16 =32, 设 {b n } 的公差为 d, 则有 解得 所以 b n =b 1 +(n-1)d=2+(n-1)×2=2n. 且数列 {b n } 的前 n 项和 T n =nb 1 + =2n+ ×2=n 2 +n. 类型二 : 等差数列、等比数列的判断 【 典例 2】 (2015 · 广东高考 ) 设数列 {a n } 的前 n 项和为 S n ,n∈N * . 已知 a 1 =1,a 2 = ,a 3 = , 且当 n≥2 时 ,4S n+2 + 5S n =8S n+1 +S n-1 . (1) 求 a 4 的值 . (2) 证明 : 为等比数列 . (3) 求数列 {a n } 的通项公式 . 【 解题指南 】 (1) 令 n=2 可得 a 4 的值 .(2) 先将 4S n+2 + 5S n =8S n+1 +S n-1 (n≥2) 转化为 4a n+2 +a n =4a n+1 (n≥2), 再利 用等比数列的定义可证 是等比数列 .(3) 先 由 (2) 可得数列 的通项公式 , 再将数列 的通项公式转化为数列 是等差数列 , 进而可得数 列 {a n } 的通项公式 . 【 解析 】 (1) 当 n=2 时 ,4S 4 +5S 2 =8S 3 +S 1 , 即 解得 :a 4 = . (2) 因为 4S n+2 +5S n =8S n+1 +S n-1 (n≥2), 所以 4S n+2 -4S n+1 +S n -S n-1 =4S n+1 -4S n (n≥2), 即 4a n+2 +a n =4a n+1 (n≥2), 因为 4a 3 +a 1 =4× +1=6=4a 2 , 所以 4a n+2 +a n =4a n+1 , 因为 所以数列 是以 a 2 - a 1 =1 为首项 , 公比为 的 等比数列 . (3) 由 (2) 知 : 数列 是以 a 2 - a 1 =1 为首项 , 公 比为 的等比数列 , 所以 即 所以数列 是以 =2 为首项 , 公差为 4 的等差数列 , 所以 =2+(n-1 ) ×4=4n-2, 即 所以数列 {a n } 的通项公式是 a n = 【 延伸探究 】 本例条件不变 , 求数列 {a n } 的前 n 项和 S n . 【 解析 】 由典例的结果 S n =a 1 +a 2 + … +a n ①-② 得 : 所以 S n = 【 规律总结 】 1. 判断一个数列为等差数列的常见方法 (1) 定义法 :a n -a n-1 =d( 常数 )(n≥2 且 n∈N * ) 等价于 {a n } 是等差数列 . (2) 等差中项法 :2a n =a n-1 +a n+1 (n≥2 且 n∈N * ) 等价于 {a n } 是等差数列 . (3) 通项公式法 :a n =kn+b(k,b 为常数 ,n∈N * ) 等价于 {a n } 是等差数列 . (4) 前 n 项和法 :S n 是 An 2 +Bn 的形式 , 等价于 {a n } 是等差数列 . 2. 判断一个数列是等比数列的常用方法 (1) 定义法 : =q(q 为常数且不为零 ,n∈N * )⇔{a n } 为等比数列 . (2) 等比中项法 :a n+1 2 =a n a n+2 (n∈N * 且 a n ≠0)⇔{a n } 为等比数列 . (3) 通项公式法 :a n =a 1 q n-1 (a 1 ≠0 且 q≠0)⇔{a n } 为等比数列 . 【 巩固训练 】 数列 {a n } 满足 a 1 =1,a 2 =2,a n+2 =2a n+1 -a n +2. (1) 设 b n =a n+1 -a n , 证明 {b n } 是等差数列 . (2) 求 {a n } 的通项公式 . 【 解析 】 (1) 由 a n+2 =2a n+1 -a n +2 得 b n+1 -b n =a n+2 -2a n+1 +a n =2a n+1 -a n +2-2a n+1 +a n =2, 所以 {b n } 是首项为 1, 公差为 2 的等差数列 . (2) 由 (1) 得 b n =2n-1, 于是 a n+1 -a n =2n-1, 当 n≥2 时 ,a n =[ (a 2 -a 1 )+(a 3 -a 2 )+ … +(a n -a n-1 )]+a 1 = [1+3+ … +(2n-3)]+1=(n-1) 2 +1 , 而 a 1 =1, 所以 {a n } 的通项公式为 a n =(n-1) 2 +1. 类型三 : 数列求和 【 典例 3】 (1) 已知等差数列 {a n } 满足 :a 3 =7,a 5 +a 7 = 26,{a n } 的前 n 项和为 S n . ① 求 a n 及 S n . ② 令 b n = (n∈N * ), 求数列 {b n } 的前 n 项和 T n . (2) 等差数列 {a n } 的前 n 项和为 S n , 等比数列 {b n } 的公比 为 , 满足 S 3 =15,a 1 +2b 1 =3,a 2 +2b 1 =6. ① 求数列 {a n },{b n } 的通项 a n ,b n . ② 求数列 {a n · b n } 的前 n 项和 T n . 【 解析 】 (1)① 设等差数列 {a n } 的首项为 a 1 , 公差为 d. 因为 a 3 =7,a 5 +a 7 =26, 所以 解得 所以 a n =3+2(n-1)=2n+1, S n =3n+ ×2=n 2 +2n. 所以 ,a n =2n+1,S n =n 2 +2n. ② 由①知 a n =2n+1, 所以 b n = 所以 T n = 即数列 {b n } 的前 n 项和 T n = . (2)① 设 {a n } 的公差为 d, 所以 解得 : a 1 =2,d=3,b 1 = , 所以 a n =3n-1,b n = . ② 由①知 T n =2× +5× +8× + … +(3n-4) · +(3n-1)× (ⅰ). (ⅰ)× 得 (ⅰ)-(ⅱ) 得 【 规律总结 】 数列求和的常见类型及方法 (1) 公式法 : 即直接利用等差数列、等比数列的前 n 项和公式求和 . ① 等差数列的前 n 项和公式 ; ② 等比数列的前 n 项和公式 . (2) 错位相减法 . 如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的 , 那么这个数列的前 n 项和即可用此法来求 , 如等比数列的前 n 项和公式就是用此法推导的 . (3) 裂项相消法 . 把数列的通项拆成两项之差 , 在求和时中间的一些项可以相互抵消 , 从而求得其和 . (4) 分组转化求和法 . 一个数列的通项公式是由若干个等差数列或等比数列或可求和的数列组成 , 则求和时可用分组求和法 , 分别求和而后相加减 . (5) 并项求和法 . 一个数列的前 n 项和中 , 可两两结合求解 , 则称之为并项求和 . 形如 a n =(-1) n f(n) 类型 , 可采用两项合并求解 . 【 巩固训练 】 1.(2016 · 石家庄高二检测 ) 等比数列 {a n } 的各项均为正数 , 且 2a 1 +3a 2 =1, a 3 2 =9a 2 a 6 . (1) 求数列 {a n } 的通项公式 . (2) 设 b n =log 3 a 1 +log 3 a 2 + … +log 3 a n , 求数列 的前 n 项和 . 【 解题指南 】 (1) 由条件求出 a 1 和 q, 再由通项公式求 a n . (2) 先求 b n , 再得出 , 利用裂项相消法求和 . 【 解析 】 (1) 设数列 {a n } 的公比为 q, 由 a 3 2 =9a 2 a 6 得 a 3 2 = 9 a 4 2 , 所以 q 2 = . 由条件可知 a n >0, 故 q= , 由 2a 1 +3a 2 =1 得 2a 1 +3a 1 q=1, 所 以 a 1 = . 故数列 {a n } 的通项公式为 a n = . (2)b n =log 3 a 1 +log 3 a 2 + … +log 3 a n =-(1+2+ … +n)= 故 所以数列 的前 n 项和为 . 2.(2016 · 六安高二检测 ) 已知公比 q>0 的等比数列 {a n } 的前 n 项和为 S n , 且 a 1 =1,S 3 =7, 数列 {b n } 中 b 1 =0,b 2 =1. (1) 若数列 {a n +b n } 是等差数列 , 求 a n ,b n . (2) 在 (1) 的条件下 , 求数列 {b n } 的前 n 项和 T n . 【 解析 】 (1) 由题意得 S 3 =1+q+q 2 =7, 所以 q=-3 或 q=2, 因为 q>0, 所以 q=2, 所以 a n =2 n-1 . 所以 a 1 +b 1 =1,a 2 +b 2 =3, 所以数列 { a n +b n } 的公差 d=2, 所以 a n +b n =2n-1. 所以 b n =2n-1-a n =(2n-1)-2 n-1 . (2) 由 (1) 得 b n =(2n-1)-2 n-1 , 所以 T n =(1-2 0 )+(3-2 1 )+(5-2 2 )+ … +[ (2n-1)-2 n-1 ] . =[1+3+5+ … +(2n-1)]-(2 0 +2 1 +2 2 + … +2 n-1 ) =n 2 -2 n +1.查看更多