2018届二轮复习(文科数学)考前冲刺练透24个高频考点学案(全国通用)
练透24个高频考点
第1讲 空间几何体的三视图、表面积与体积
考点一 集合的运算
1.已知集合A={x|2
5},则A∩B=( )
A.{x|25}
C.{x|25}
2.设全集U={x∈N|x≤8},集合A={1,3,7},B={2,3,8},则(∁UA)∩(∁UB)=( )
A.{1,2,7,8} B.{4,5,6} C.{0,4,5,6} D.{0,3,4,5,6}
3.设全集U=R,集合A={x|0≤x≤2},B={y|1≤y≤3},则(∁UA)∪B=( )
A.(2,3] B.(-∞,1]∪(2,+∞)
C.[1,2) D.(-∞,0)∪[1,+∞)
4.设集合A=,B={x|y=ln(x2-3x)},则A∩B中元素的个数是( )
A.1 B.2 C.3 D.4
考点二 复数
1.=( )
A.-1-i B.-1+i
C.1+i D.1-i
2.复数z=的虚部为( )
A.-1 B.-3 C.1 D.2
3.已知复数z满足=-i,则|z|=( )
A.1 B.
C.2 D.2
4.在复平面内,复数对应的点在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
5.复数(1+i)2+的共轭复数是( )
A.1+i B.1-i C.-1+i D.- 1-i
6.已知i为虚数单位,若实数a,b满足(a+bi)i=1+i,则a+bi的模为( )
A.1 B. C. D.2
考点三 程序框图
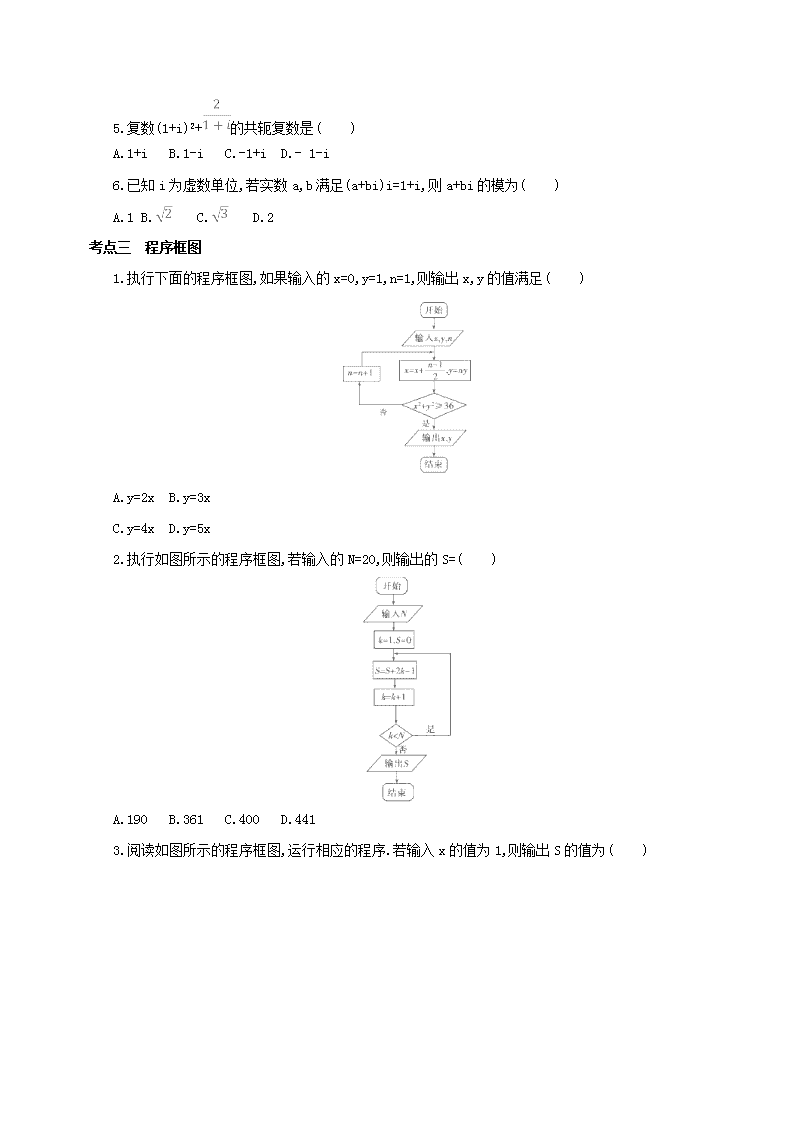
1.执行下面的程序框图,如果输入的x=0,y=1,n=1,则输出x,y的值满足( )
A.y=2x B.y=3x
C.y=4x D.y=5x
2.执行如图所示的程序框图,若输入的N=20,则输出的S=( )
A.190 B.361 C.400 D.441
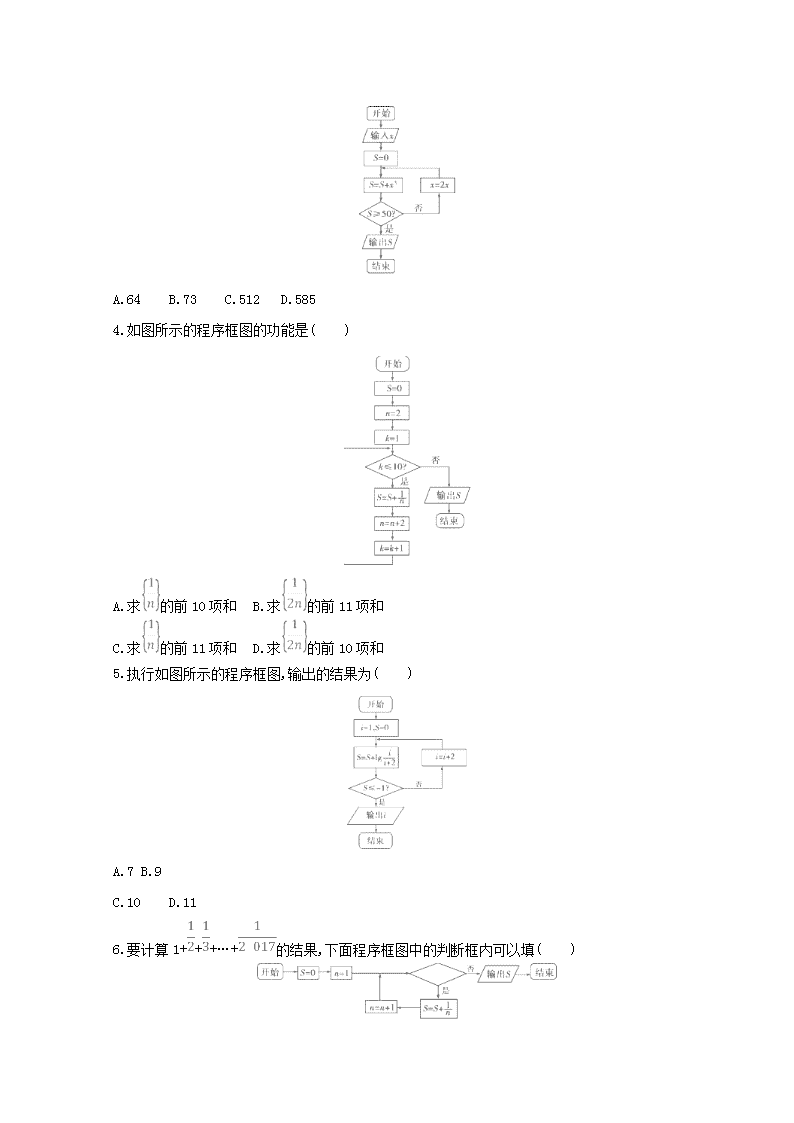
3.阅读如图所示的程序框图,运行相应的程序.若输入x的值为1,则输出S的值为( )
A.64 B.73 C.512 D.585
4.如图所示的程序框图的功能是( )
A.求的前10项和 B.求的前11项和
C.求的前11项和 D.求的前10项和
5.执行如图所示的程序框图,输出的结果为( )
A.7 B.9
C.10 D.11
6.要计算1+++…+的结果,下面程序框图中的判断框内可以填( )
A.n<2 017 B.n≤2 017
C.n>2 017 D.n≥2 017
考点四 三角函数
1.已知角φ的终边经过点P(-4,3),函数f(x)=sin(ωx+φ)(ω>0)的图象的相邻两条对称轴之间的距离等于,则f的值为( )
A. B.
C.- D.-
2.函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤π)的部分图象如图所示,其中A,B两点之间的距离为5,则f(x)的单调递增区间是( )
A.[6k-1,6k+2](k∈Z) B.[6k-4,6k-1](k∈Z)
C.[3k-1,3k+2](k∈Z) D.[3k-4,3k-1](k∈Z)
3.已知函数f(x)=sin 2x+2cos2x,下列结论正确的是( )
A.函数f(x)的最小正周期为2π
B.函数f(x)在区间上单调递增
C.函数f(x)的图象关于直线x=对称
D.函数f(x)的图象关于点对称
4.已知函数f(x)=sin ωx-cos ωx(ω>0)在(0,π)上有且只有两个零点,则实数ω的取值范围为( )
A. B.
C. D.
5.已知函数f(x)=sin(0<ω<2)满足条件:f=0,为了得到y=f(x)的图象,可将函数g(x)=cos ωx的图象向右平移m个单位长度(m>0),则m的值可以为( )
A.1 B. C. D.
6.已知函数f(x)=4sin3xcos x-2sin xcos x-cos 4x.
(1)求函数f(x)的最小正周期及单调递增区间;
(2)求f(x)在区间上的最大值和最小值.
考点五 解三角形
1.在△ABC中,角A,B,C的对边分别为a,b,c,若a=b,A=2B,则cos B等于( )
A. B. C. D.
2.在锐角△ABC中,AB=3,AC=4,S△ABC=3,则BC=( )
A.5 B.或 C. D.
3.如图,在△ABC中,∠B=45°,D是BC边上一点,AD=5,AC=7,DC=3,则AB的长为 .
4.△ABC的内角A,B,C的对边分别为a,b,c.已知B=2C,2b=3c.
(1)求cos C;
(2)若c=4,求△ABC的面积.
5.如图,在平面四边形ABCD中,AB⊥BC,AB=2,BD=,∠BCD=2∠ABD,△ABD的面积为2.
(1)求AD的长;
(2)求△CBD的面积.
考点六 平面向量
1.已知向量m=(λ+1,1),n=(λ+2,2),若(m+n)⊥(m-n),则λ的值为( )
A.0 B.-1 C.-2 D.-3
2.在平面直角坐标系xOy中,已知四边形ABCD是平行四边形,=(1,-2),=(2,1),则·=( )
A.5 B.4 C.3 D.2
3.在梯形ABCD中,AD∥BC,已知AD=4,BC=6,若=m+n(m,n∈R),则=( )
A.-3 B.- C. D.3
4.如图所示,正方形ABCD的边长为2,圆D的半径为1,E是圆D上任意一点,则·的最小值为( )
A.1+2 B.-1-2
C.1- D.1-2
5.矩形ABCD中,AB=3,AD=2,P为矩形内部一点,且AP=1,若=x+y,则3x+2y的取值范围是 .
考点七 等差数列
1.在等差数列{an}中,若a4+a9+a14=36,则2a10-a11=( )
A.6 B.12 C.24 D.36
2.设Sn是等差数列{an}的前n项和,若S1 009-S1 007=2,则S2 016=( )
A.1 008 B.1 009
C.2 016 D.2 017
3.已知{an}为等差数列,Sn为其前n项和,公差为d.若-=100,则d的值为( )
A. B. C.10 D.20
4.在我国古代著名的数学专著《九章算术》里有一段叙述:今有良马与驽马发长安至齐,齐去长安一千一百二十五里,良马初日行一百零三里,日增十三里;驽马初日行九十七里,日减半里;良马先至齐,复还迎驽马,二马相逢,问:几日相逢?( )
A.12日 B.16日
C.8日 D.9日
5.设等差数列{an}的前n项和为Sn,等差数列{bn}的前n项和为Tn,若=,则+= .
考点八 等比数列
1.在等比数列{an}中,Sn表示前n项和,若a3=2S2+1,a4=2S3+1,则公比q等于( )
A.-3 B.-1 C.1 D.3
2.在正项等比数列{an}中,a1=1,前n项和为Sn,且-a3,a2,a4成等差数列,则S7的值为( )
A.125 B.126 C.127 D.128
3.已知Sn是各项均为正数的等比数列{an}的前n项和,若a2·a4=16,S3=7,则a8=( )
A.32 B.64 C.128 D.256
4.数列{an}满足:an+1=λan-1(n∈N ,且λ∈R且λ≠0),若数列{an-1}是等比数列,则λ的值等于( )
A.1 B.-1 C. D.2
5.Sn为等比数列{an}的前n项和,满足Sn=2an-1,则数列{an}的公比q= .
6.《九章算术》中的“两鼠穿墙”是我国数学的古典名题:“今有垣厚若干尺,两鼠对穿,大鼠日一尺,小鼠也日一尺,大鼠日自倍,小鼠日自半,问何日相逢?各穿几何?”题意是:“有两只老鼠从墙的两边打洞穿墙,大老鼠第一天进一尺,以后每天加倍;小老鼠第一天也进一尺,以后每天减半.”如果墙足够厚,Sn为前n天两只老鼠打洞厚度之和,则Sn= 尺.
考点九 数列通项与前n项和
1.已知等比数列{an}的前n项和Sn=2n+1+a,数列{bn}满足bn=2-log2.
(1)求常数a的值;
(2)求数列{bn}的前n项和Tn.
2.已知数列{an}的前n项和为Sn,且Sn=2an-2(n∈N ).
(1)求数列{an}的通项公式;
(2)求数列{Sn}的前n项和Tn.
3.已知等差数列{an}的前n项和为Sn,且a1=1,S3+S4=S5.
(1)求数列{an}的通项公式;
(2)令bn=(-1)n-1an,求数列{bn}的前2n项和T2n.
4.已知数列{an}是公差不为0的等差数列,首项a1=1,且a1,a2,a4成等比数列.
(1)求数列{an}的通项公式;
(2)设数列{bn}满足bn=an+,求数列{bn}的前n项和Tn.
5.已知等差数列{an}的前n项和为Sn,若Sm-1=-4,Sm=0,Sm+2=14(m≥2,且m∈N ).
(1)求m的值;
(2)若数列{bn}满足=log2bn(n∈N ),求数列{(an+6)·bn}的前n项和.
考点十 简单的线性规划问题
1.若实数x,y满足约束条件则x-2y的最大值为( )
A.-9 B.-3 C.-1 D.3
2.设x,y满足约束条件若z=x+3y的最大值与最小值的差为7,则实数m=( )
A. B.-
C. D.-
3.设变量x,y满足不等式组则x2+y2的最小值是( )
A. B.
C. D.2
4.当x,y满足不等式组时,-2≤kx-y≤2恒成立,则实数k的取值范围是( )
A.[-1,1] B.[-2,0]
C. D.
5.如果实数x,y满足条件则z=的最大值为 .
考点十一 空间几何体的三视图、表面积和体积
1.某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为( )
A.1 B.
C. D.2
2.如图, 格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则此几何体的体积为( )
A.12 B.18
C.24 D.30
3.如图, 格纸上的小正方形的边长为1,粗实线画出的是一个几何体的三视图,则该几何体的体积是( )
A.4+6π B.8+6π C.4+12π D.8+12π
4.某几何体的三视图如图所示(在 格线中,每个小正方形的边长为1),则该几何体的体积为( )
A.2 B.3 C.4 D.5
5.下图是一几何体的三视图,则该几何体的表面积是( )
A.5+ B.5+2
C.4+2 D.4+2
考点十二 球
1.正四棱锥的顶点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为( )
A. B.16π C.9π D.
2.某几何体的三视图如图所示,则该几何体外接球的表面积为( )
A.4π B.12π C.24π D.48π
3.设三棱柱的侧棱垂直于底面,所有棱的长都为a,顶点都在一个球面上,则该球的表面积为 .
4.已知三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD,BC=CD=1,AB=,则该三棱锥外接球的体积为 .
考点十三 空间位置关系的证明
1.如图所示的空间几何体ABCDEFG中,四边形ABCD是边长为2的正方形,AE⊥平面ABCD,EF∥AB,EG∥AD,EF=EG=1.
(1)求证:平面CFG⊥平面ACE;
(2)在AC上是否存在一点H,使得EH∥平面CFG?若存在,求出CH的长;若不存在,请说明理由.
2.在四棱锥S-ABCD中,底面ABCD为平行四边形,∠DBA=60°,∠SAD=30°,AD=SD=2,BA=BS=4.
(1)证明:BD⊥平面SAD;
(2)求点C到平面SAB的距离.
3.如图,在几何体ABCDEF中,四边形ABCD是菱形,BE⊥平面ABCD,DF∥BE,且DF=2BE=2,EF=3.
(1)证明:平面ACF⊥平面BEFD;
(2)若cos∠BAD=,求几何体ABCDEF的体积.
4.如图,在高为1的等腰梯形ABCD中,AM=CD=AB=1,M为AB的三等分点.现将△AMD沿MD折起,使平面AMD⊥平面MBCD,连接AB、AC.
(1)在AB边上是否存在点P,使AD∥平面MPC?
(2)当点P为AB边的中点时,求点B到平面MPC的距离.
考点十四 圆
1.过点P(4,2)作圆x2+y2=4的两条切线,切点分别为A、B,O为坐标原点,则△OAB外接圆的方程是( )
A.(x-2)2+(y-1)2=5 B.(x-4)2+(y-2)2=20
C.(x+2)2+(y+1)2=5 D.(x+4)2+(y+2)2=20
2.经过原点并且与直线x+y-2=0相切于点(2,0)的圆的标准方程是( )
A.(x-1)2+(y+1)2=2 B.(x+1)2+(y-1)2=2
C.(x-1)2+(y+1)2=4 D.(x+1)2+(y-1)2=4
3.已知圆的半径为2,圆心在x轴的正半轴上,且与直线3x+4y+4=0相切,则圆的方程是( )
A.x2+y2-4x=0 B.x2+y2+4x=0
C.x2+y2-2x-3=0 D. x2+y2+2x-3=0
4.过点(1,-2)作圆(x-1)2+y2=1的两条切线,切点分别为A、B,则AB所在直线的方程为( )
A.y=- B.y=-
C.y=- D.y=-
5.已知圆C经过点A(2,0)、B(1,-),且圆心C在直线y=x上.
(1)求圆C的方程;
(2)过点的直线l被圆截得的弦长为2,求直线l的方程.
考点十五 圆锥曲线的标准方程与几何性质
1.已知焦点在x轴上的椭圆的离心率为,且它的长轴长等于圆C:x2+y2-2x-15=0的半径,则椭圆的标准方程是( )
A.+=1 B.+=1 C.+y2=1 D.+=1
2.已知双曲线-=1(a>0,b>0)的一个焦点与抛物线y2=4x的焦点重合,且双曲线的离心率等于,则该双曲线的方程为( )
A.5x2-=1 B.-=1
C.-=1 D.5x2-=1
3.当双曲线M:-=1(-2≤m<0)的焦距取得最小值时,双曲线M的渐近线方程为( )
A.y=±x B.y=±x
C.y=±2x D.y=±x
4.已知F是抛物线x2=4y的焦点,P为抛物线上的动点,且A的坐标为(0,-1),则的最小值是( )
A. B. C. D.
5.如图,在平面直角坐标系xOy中,F是椭圆+=1(a>b>0)的右焦点,直线y=与椭圆交于B,C两点,且∠BFC=90°,则该椭圆的离心率是 .
考点十六 圆锥曲线的综合问题
1.已知椭圆的一个焦点与抛物线y2=4x的焦点相同,且该椭圆的离心率为.
(1)求椭圆的标准方程;
(2)过点P(0,1)的直线与该椭圆交于A,B两点,O为坐标原点,若=2,求△AOB的面积.
2.已知椭圆E:+=1(a>b>0)经过点M,离心率为.
(1)求椭圆E的标准方程;
(2)若A1,A2分别是椭圆E的左、右顶点,过点A2作直线l与x轴垂直,点P是椭圆E上的任意一点(不同于椭圆E的四个顶点),连接PA1交直线l于点B,点Q为线段A2B的中点,求证:直线PQ与椭圆E只有一个公共点.
3.设椭圆E:+=1(a>b>0)的右焦点为F,右顶点为A,B,C是椭圆上关于原点对称的两点(B,C均不在x轴上),线段AC的中点为D,且B,F,D三点共线.
(1)求椭圆E的离心率;
(2)设F(1,0),过F的直线l交E于M,N两点,直线MA,NA分别与直线x=9交于P,Q两点.证明:以PQ为直径的圆过点F.
4.已知椭圆E的中心在坐标原点,焦点F1,F2在y轴上,离心率等于,P是椭圆E上的点.以线段PF1为直径的圆经过F2,且9·=1.
(1)求椭圆E的方程;
(2)作直线l与椭圆E交于两个不同的点M,N.如果线段MN被直线2x+1=0平分,求直线l的倾斜角的取值范围.
考点十七 函数的概念与性质
1.已知函数f(x)=(a∈R),若f [f(-1)]=1,则a=( )
A. B. C.1 D.2
2.若函数f(x)=ax3+bx+2(a,b为常数)在(-∞,0)上有最小值-5,则函数f(x)在(0,+∞)上( )
A.有最大值5 B.有最小值5
C.有最大值3 D.有最大值9
3.已知a=,b=,c=,则( )
A.a0,且a≠1),若f(x)>1在区间[1,2]上恒成立,则实数a的取值范围为 .
考点十八 函数与方程
1.函数f(x)=|x-2|-ln x在定义域内的零点的个数为( )
A.0 B.1 C.2 D.3
2.若函数f(x)=3ax+1-2a在区间(-1,1)内存在一个零点,则a的取值范围是( )
A.a> B.a>或a<-1
C.-10时,xf '(x)-f(x)>0,则使得f(x)>0成立的x的取值范围是 .
5.已知函数f(x)=ax2+bx+xln x的图象在(1, f(1))处的切线方程为3x-y-2=0.
(1)求实数a,b的值;
(2)设g(x)=x2-x,若k∈Z,且k(x-2)2恒成立,求k的最大值.
6.已知函数f(x)=aln x+x2-ax(a∈R).
(1)若x=3是f(x)的极值点,求f(x)的单调区间;
(2)求g(x)=f(x)-2x在区间[1,e]上的最小值h(a).
答案全解全析
考点一 集合的运算
1.C 将集合A、B画在数轴上,如图.
由图可知A∩B={x|22或x<0},B={y|1≤y≤3},所以(∁UA)∪B=(-∞,0)∪[1,+∞).
4.A A=={x∈N|-2≤x≤4}={0,1,2,3,4},B={x|y=ln(x2-3x)}={x|x2-3x>0}={x|x<0或x>3},故A∩B={4},元素个数为1.
考点二 复数
1.B ====-1+i,故选B.
2.B z====1-3i.
3.A 由题意知z===i,则|z|=1.故选A.
4.B ==,故其对应的点在第二象限,选B.
5.B 因为(1+i)2+=2i+=2i+1-i=1+i,所以复数(1+i)2+的共轭复数是1-i,选B.
6.B 依题意得a+bi==1-i,所以|a+bi|=|1-i|=,故选B.
考点三 程序框图
1.C 执行程序框图:当n=1时,x=0,y=1,
此时02+12≥36不成立;当n=2时,x=,y=2,
此时+22≥36不成立;当n=3时,x=,y=6,
此时+62≥36成立,结束循环,输出x的值为,
y的值为6,满足y=4x,故选C.
2.B 当输入的N=20时,输出的S的值是数列{2k-1}的前19项和,即=361,选B.
3.B 由程序框图,可得x=1,S=1;x=2,S=1+23=9;x=4,S=9+43=73.循环结束,故输出的S为73.
4.D 依题意可得S=+++…+,故程序框图的功能是求的前10项和,选D.
5.B 程序框图的运行过程如下:
i=1,S=lg=-lg 3>-1,否;
i=3,S=lg+lg=lg=-lg 5>-1,否;
i=5,S=lg+lg=lg=-lg 7>-1,否;
i=7,S=lg+lg=lg=-lg 9>-1,否;
i=9,S=lg+lg=lg=-lg 11<-1,是,输出i=9.故选B.
6.B 题中所给的程序框图中的循环结构为当型循环,累加变量初始值为0,计数变量初始值为1,要求S=0+1+++…+的值,共需要计算2 017次,故选B.
考点四 三角函数
1.D 由角φ的终边经过点P(-4,3),
可得cos φ=,sin φ=.
根据函数f(x)=sin(ωx+φ)(ω>0)的图象的相邻两条对称轴之间的距离等于,可得周期为=2×,
解得ω=2,
∴f(x)=sin(2x+φ),
∴f=sin=cos φ=-.故选D.
2.B |AB|=5,|yA-yB|=4,所以|xA-xB|=3,即=3,T=6,所以ω==.
因为f(x)=2sin的图象过点(2,-2),即2sin=-2,
所以sin=-1,
因为0≤φ≤π,所以+φ=,解得φ=,故f(x)=2sin,由2kπ-≤x+≤2kπ+,k∈Z,得6k-4≤x≤6k-1,k∈Z,
故函数f(x)的单调递增区间为[6k-4,6k-1](k∈Z).故选B.
3.C f(x)=sin 2x+2cos2x=sin 2x+cos 2x+1=2sin+1.函数f(x)的最小正周期T==π,A错误;当0),由题意,知2a2=a4-a3,又a1=1,∴2q=q3-q2,解得q=2或q=-1(舍去),∴S7==127,故选C.
3.C 设公比为q,由题意知q≠1.
∵a2·a4==16,∴a3=4(负值舍去),
∵a3=a1q2=4,S3=7,∴S2==3,∴(1-q2)=3(1-q),即3q2-4q-4=0,解得q=-或q=2,∵an>0,∴q=2,∴a1=1,∴a8=27=128.
4.D 由an+1=λan-1,得an+1-1=λan-2=λ.由于数列{an-1}是等比数列,所以=1,解得λ=2.
5.答案 2
解析 由Sn=2an-1,得a1=2a1-1,a1+a2=2a2-1,解得a1=1,a2=2.∴等比数列{an}的公比q=2.
6.答案 2n-+1
解析 由题意,知大老鼠所穿墙的厚度构成首项为1,公比为2的等比数列,小老鼠所穿墙的厚度构成首项为1,公比为的等比数列,故Sn=+=2n-+1.
考点九 数列通项与前n项和
1.解析 (1)当n=1时,a1=S1=22+a=4+a,
当n≥2时,an=Sn-Sn-1=2n+1+a-(2n+a)=2n,
∵{an}为等比数列,∴=a1·a3,即(22)2=(4+a)·23,
解得a=-2.
(2)由(1)知,an=2n,n∈N ,则bn=2-log223n=2-3n,
∵bn+1-bn=-3对一切n∈N 都成立,
∴{bn}是以-1为首项,-3为公差的等差数列,
∴Tn=nb1+d=.
2.解析 (1)当n=1时,S1=2a1-2,即a1=2a1-2,解得a1=2.
当n≥2时,an=Sn-Sn-1=(2an-2)-(2an-1-2),
即an=2an-1,
所以数列{an}是首项为2,公比为2的等比数列.
所以an=2×2n-1=2n.
(2)由(1),知Sn=2an-2=2n+1-2,
所以Tn=S1+S2+…+Sn
=22+23+…+2n+1-2n
=-2n
=2n+2-4-2n.
3.解析 (1)设等差数列{an}的公差为d,
由S3+S4=S5,可得a1+a2+a3=a5,即3a2=a5,
∴3(1+d)=1+4d,解得d=2.
∴an=1+(n-1)×2=2n-1.
(2)由(1),可得bn=(-1)n-1·(2n-1).
∴T2n=1-3+5-7+…+(2n-3)-(2n-1)
=-2n.
4.解析 (1)设数列{an}的公差为d,由已知得,=a1a4,
即(1+d)2=1+3d,解得d=0或d=1.
又d≠0,∴d=1,可得an=n.
(2)由(1)得bn=n+2n,
∴Tn=(1+21)+(2+22)+(3+23)+…+(n+2n)
=(1+2+3+…+n)+(21+22+23+…+2n)
=+2n+1-2.
5.解析 (1)由已知得,am=Sm-Sm-1=4,
且am+1+am+2=Sm+2-Sm=14,
设数列{an}的公差为d,则有2am+3d=14,
∴d=2.
由Sm=0,得ma1+×2=0,即a1=1-m,
∴am=a1+(m-1)×2=m-1=4,
∴m=5.
(2)由(1)知a1=-4,d=2,∴an=2n-6,
∴n-3=log2bn,得bn=2n-3,
∴(an+6)·bn=2n×2n-3=n×2n-2.
设数列{(an+6)·bn}的前n项为Tn,
则Tn=1×2-1+2×20+…+(n-1)×2n-3+n×2n-2,①
2Tn=1×20+2×21+…+(n-1)×2n-2+n×2n-1,②
①-②,得-Tn=2-1+20+…+2n-2-n×2n-1
=-n×2n-1
=2n-1--n×2n-1,
∴Tn=(n-1)×2n-1+(n∈N ).
考点十 简单的线性规划问题
1.C 画出可行域,如图中阴影部分所示,令z=x-2y,可知z=x-2y在点(1,1)处取得最大值-1,故选C.
2.C 由约束条件作出可行域如图,
联立解得A(1,2),
联立解得B(m-1,m),化z=x+3y,为y=-+.
由图可知,当直线y=-+过点A时,z有最大值,为7,
当直线y=-+过点B时,z有最小值,为4m-1,
由题意得7-(4m-1)=7,解得m=.
故选C.
3.B 根据题意画出可行域,如图所示,x2+y2表示可行域内的点到原点的距离的平方,其距离的最小值为原点到直线x+y=3的距离.∵原点到直线x+y=3的距离为=,∴x2+y2的最小值为.
4.D 作出不等式组表示的平面区域,如图中阴影部分所示,
设z=kx-y,由
得即B(-2,2),
由得即C(2,0),
由得即A(-5,-1),要使不等式-2≤kx-y≤2恒成立,则即所以-≤k≤0,故选D.
5.答案
解析 z==2-,根据约束条件画出可行域(图略),当x=,y=1时,取得最小值,则z的最大值为.
考点十一 空间几何体的三视图、表面积和体积
1.C 四棱锥的直观图如图所示,PC⊥平面ABCD,PC=1,底面四边形ABCD是边长为1的正方形,故该四棱锥最长棱的棱长为PA==.
2.C 由三视图知,该几何体是直三棱柱削去一个同底的三棱锥,其中三棱柱的高为5,削去的三棱锥的高为3,三棱锥与三棱柱的底面均为两直角边长分别为3和4的直角三角形,所以该几何体的体积为×3×4×5-××3×4×3=24,故选C.
3.B 该几何体为四棱锥与半个圆柱的组合体,其中半个圆柱的底面直径为4,母线长为3,四棱锥的底面是长为4,宽为3的矩形,高为2,所以该几何体的体积为V=×π×22×3+×4×3×2=8+6π,选B.
4.A 由三视图知,该几何体为四棱锥,其底面面积S=×(1+2)×2=3,高为2,所以该几何体的体积V=×3×2=2,故选A.
5.A 由三视图可知该几何体的直观图如图所示,是一个六面体ABCDEFG,其中底面ABCD为正方形,AF∥CG,且AF=CG=1,DE∥AF,且DE=2AF,易计算出EF=BF=BG=EG=,所以四边形EFBG为菱形,其对角线长分别为和,故该几何体的表面积S=1×1+×1×1×2+×(1+2)×1×2+××=5+,故选A.
考点十二 球
1.A 易知球心在正四棱锥的高上,设球的半径为R,则(4-R)2+()2=R2,解得R=,所以该球的表面积为4π×=,故选A.
2.B 由三视图可知该几何体为三棱锥P-ABC,其中,PA⊥平面ABC,AB⊥BC,PA=AB=BC=2,AC=2,则PC==2.
取PC的中点O,AC的中点D,
连接OA,OD,BD,OB.
∴OP=OC=,OA=PC=,BD=AC=,OD=PA=1.
易知OD⊥平面ABC,∴OB==,
∴OA=OB=OC=OP,
∴O是三棱锥P-ABC外接球的球心,外接球半径r=OA=,
∴该几何体外接球的表面积S=4πr2=12π.故选B.
3.答案 πa2
解析 由题意知,该三棱柱为正三棱柱,且侧棱与底面边长相等,均为a.设O,O1分别为下、上底面中心,且球心O2为O1O的中点,
又AD=a,AO=a,OO2=,设球的半径为R,则R2=A=a2+a2=a2.
所以S球=4πR2=4π×a2=πa2.
4.答案 π
解析 因为BC=1,CD=1,BC⊥CD,所以BD=,又AB=,且AB⊥平面BCD,所以AD=2,AB⊥CD,又AB∩BC=B,所以CD⊥平面ABC,所以CD⊥AC,所以三棱锥A-BCD的外接球的球心为AD的中点,半径为1,所以三棱锥A-BCD的外接球的体积为.
考点十三 空间位置关系的证明
1.解析 (1)证明:连接BD交AC于点O,则BD⊥AC.
设AB,AD的中点分别为M,N,连接MN,则MN∥BD.
连接FM,GN.
则FM∥GN,且FM=GN,所以四边形FMNG是平行四边形,
所以MN∥FG,所以BD∥FG,
因为AE⊥平面ABCD,所以AE⊥BD.
所以FG⊥AC,FG⊥AE,又AC∩AE=A,
所以FG⊥平面ACE,
又FG⊂平面CFG,所以平面CFG⊥平面ACE.
(2)存在.设平面ACE交FG于点Q,则Q为FG的中点,连接EQ,CQ,取CO的中点H,连接EH.易知CH∥EQ,CH=EQ=,所以四边形EQCH为平行四边形,所以EH∥CQ,又EH⊄平面CFG,CQ⊂平面CFG,所以EH∥平面CFG.
所以在AC上存在一点H,使得EH∥平面CFG,且CH=.
2.解析 (1)证明:在△ABD中,由正弦定理得=,
∵∠DBA=60°,AD=2,AB=4,
∴sin∠ADB=1,∴∠ADB=90°,
即BD⊥AD.∴BD=2.
在△SBD中,∵SD=2,BS=4,BD=2,
∴DB2+SD2=BS2,∴BD⊥SD.
又SD∩AD=D,∴BD⊥平面SAD.
(2)由题意可知,CD∥AB,
∵AB⊂平面SAB,CD⊄平面SAB,
∴CD∥平面SAB,则点C到平面SAB的距离等于点D到平面SAB的距离,设点C到平面SAB的距离为h,
易求得SA=6,
S△SAD=×2×2×sin 120°=3,
且S△SAB=×6×=3,
∵BD⊥平面SAD,∴BD是三棱锥B-SAD的高,
∵VB-SAD=VD-SAB,即×3×2=×3×h,
∴h=,
故点C到平面SAB的距离为.
3.解析 (1)证明:∵四边形ABCD是菱形,
∴AC⊥BD.
∵BE⊥平面ABCD,∴BE⊥AC.
又BE∩BD=B,
∴AC⊥平面BEFD.
又AC⊂平面ACF,
∴平面ACF⊥平面BEFD.
(2)设AC与BD的交点为O,AB=a(a>0),
由(1)得AC⊥平面BEFD.
∵BE⊥平面ABCD,∴BE⊥BD,
∵DF∥BE,∴DF⊥BD,
∴BD2=EF2-(DF-BE)2=8,∴BD=2,
∴S四边形BEFD=(BE+DF)·BD=3,
∵cos∠BAD=,
∴BD2=AB2+AD2-2AB·AD·cos∠BAD=a2=8,
∴a=,∴OA2=AB2-OB2=3,∴OA=,
∴VABCDEF=2VA-BEFD=S四边形BEFD·OA=2.
4.解析 (1)存在.当AP=AB时,有AD∥平面MPC.理由如下:
连接BD交MC于N,连接NP.
在梯形MBCD中,∵DC∥MB,∴==.
在△ADB中,∵=,∴AD∥PN.
∵AD⊄平面MPC, PN⊂平面MPC,
∴AD∥平面MPC.
(2)∵平面AMD⊥平面MBCD,平面AMD∩平面MBCD=DM,
AM⊥DM,∴AM⊥平面MBCD.
∴VP-MBC=×S△MBC×=××2×1×=.
△MPC中, MP=AB=,
MC=, 又PC==,
∴S△MPC=××=,
设点B到平面MPC的距离为d,
∵VP-MBC=VB-PMC,
∴点B到平面MPC的距离d===.
考点十四 圆
1.A 由题意知O、A、B、P四点共圆,从而OP的中点坐标(2,1)为所求圆的圆心,|OP|=为所求圆的半径,所以所求圆的方程为(x-2)2+(y-1)2=5.故选A.
2.A 设圆心的坐标为(a,b),圆的半径为r,
则a2+b2=r2①,
(a-2)2+b2=r2②,
=1③,
联立①②③解得a=1,b=-1,r2=2.
故所求圆的标准方程是(x-1)2+(y+1)2=2.故选A.
3.A 设圆心为C(m,0)(m>0),因为所求圆与直线3x+4y+4=0相切,所以=2,整理得|3m+4|=10,解得m=2或m=-(舍去),故所求圆的方程为(x-2)2+y2=4,即x2+y2-4x=0,故选A.
4.B 圆(x-1)2+y2=1的圆心为(1,0),半径为1,
以(1,0),(1,-2)为直径两端点的圆的方程为(x-1)2+(y+1)2=1,
将两圆的方程相减得AB所在直线的方程为2y+1=0,
即y=-.故选B.
5.解析 (1)由题易求得AB的中点坐标为,AB所在直线的斜率为,
可得AB的垂直平分线的方程为x+3y=0,其与x-y=0的交点为(0,0),∴圆心坐标为(0,0),则圆的半径为2,
∴圆C的方程为x2+y2=4.
(2)当直线l的斜率存在时,设直线l的斜率为k,
又直线l过点,
∴直线l的方程为y-=k(x-1),
即y=kx+-k,
则圆心(0,0)到直线l的距离d=,
又圆的半径r=2,弦长为2,
所以+()2=4,
解得k=-,
则直线l的方程为y=-x+.
当直线l的斜率不存在时,直线l的方程为x=1,满足题意.
综上可得,直线l的方程为x=1或y=-x+.
考点十五 圆锥曲线的标准方程与几何性质
1.A 设椭圆的标准方程为+=1(a>0,b>0).由x2+y2-2x-15=0,知圆的半径为4,则2a=4,所以a=2.
又e==,所以c=1,
则b2=a2-c2=3.因此椭圆的标准方程为+=1.
2.D ∵抛物线的焦点为(1,0),
∴c=1,又=,
∴a=,∴b2=c2-a2=1-=.
故所求双曲线的方程为5x2-=1,故选D.
3.C 由题意可得2c=2=2(-2≤m<0),当m=-1时,焦距2c取得最小值,此时双曲线M的方程为x2-=1,所以所求的渐近线方程为y=±2x,故选C.
4.C 抛物线的准线为l:y=-1,过点P作PD⊥l于D,
则|PD|=|PF|,且点A在准线上,
如图所示,所以==sin∠PAD,
当直线PA与抛物线相切时,==sin∠PAD有最小值,由y=得y'=,
设切点为(x0>0),
则=,
解得x0=2,此时∠PAD=,
所以=sin=,故选C.
5.答案
解析 由已知条件易得B,C,
F(c,0),∴=,=,
由∠BFC=90°,可得·=0,
所以+=0,
c2-a2+b2=0,
即4c2-3a2+(a2-c2)=0,
亦即3c2=2a2,
所以=,则e==.
考点十六 圆锥曲线的综合问题
1.解析 (1)依题意,设椭圆的标准方程为+=1(a>b>0),
由题意可得c=,又e==,∴a=2.
∴b2=a2-c2=2,
∴椭圆的标准方程为+=1.
(2)设A(x1,y1),B(x2,y2),
由=2,得
设直线AB的方程为y=kx+1,代入椭圆方程整理,得
(2k2+1)x2+4kx-2=0,∴x1+x2=-.x1·x2=.
则有=,
解得k2=.
∴△AOB的面积S=|OP|·|x1-x2|==·=.
2.解析 (1)依题意得,⇒
∴椭圆E的标准方程为+=1.
(2)证明:设P(x0,y0)(x0≠0且x0≠±),则直线PA1的方程为y=(x+),
令x=,得B,则线段A2B的中点Q,∴直线PQ的斜率kPQ==.①
∵P是椭圆E上的点,∴=3,代入①式,得kPQ=-,
∴直线PQ的方程为y-y0=- (x-x0),
联立,得
又2+3=6,整理得x2-2x0x+=0,
∵Δ=0,∴直线PQ与椭圆E相切,即直线PQ与椭圆E只有一个公共点.
3.解析 (1)解法一:由题意可知A(a,0),F(c,0),设B(x0,y0),C(-x0,-y0),则D,
∵B,F,D三点共线,∴∥,
又=(c-x0,-y0),=,
∴-y0(c-x0)=-y0·,
∴a=3c,从而e=.
解法二:连接OD,AB,由题意知,OD是△CAB的中位线,
∴OD∥AB,OD=AB,
∴△OFD∽△AFB.
∴=,解得a=3c,从而e=.
(2)证明:∵F的坐标为(1,0),
∴c=1,从而a=3,∴b2=8.
∴椭圆E的方程为+=1.
设直线l的方程为x=ny+1,
由⇒(8n2+9)y2+16ny-64=0,
∴y1+y2=,y1y2=,
其中M(ny1+1,y1),N(ny2+1,y2).
∴直线AM的方程为=,
∴P, 同理,Q,
从而·=·
=64+
=64+
=64+=0.
∴FP⊥FQ,即以PQ为直径的圆恒过点F.
4.解析 (1)依题意,设椭圆E的方程为+=1(a>b>0),半焦距为c.
∵椭圆E的离心率等于,
∴c=a,则b2=a2-c2=.
∵以线段PF1为直径的圆经过F2,
∴PF2⊥F1F2.
∴|PF2|=.
∵9·=1,∴9||2==1.
由得
∴椭圆E的方程为+x2=1.
(2)∵直线x=-与x轴垂直,且由已知得直线l与直线x=-相交,
∴直线l不可能与x轴垂直,
∴设直线l的方程为y=kx+m.
由得(k2+9)x2+2kmx+(m2-9)=0.
∵直线l与椭圆E交于两个不同的点M,N,
∴Δ=4k2m2-4(k2+9)(m2-9)>0,
即m2-k2-9<0.
设M(x1,y1),N(x2,y2),则x1+x2=-.
∵线段MN被直线2x+1=0平分,
∴2×+1=0,
即-+1=0.
由得-(k2+9)<0.
∵k2+9>0,∴-1<0,
∴k2>3,解得k>或k<-.
∴直线l的倾斜角的取值范围为∪.
考点十七 函数的概念与性质
1.A 由f[f(-1)]=f(2)=4a=1,得a=,故选A.
2.D 令g(x)=ax3
+bx,则函数g(x)为奇函数,则由题意可知g(x)在(0,+∞)上有最大值7,因为f(x)=g(x)+2,所以f(x)在(0,+∞)上有最大值9,选D.
3.D ∵y=为减函数,>,∴b,∴a>c,∴b1时, f(x)=loga(8-ax)在[1,2]上是减函数,由于f(x)>1恒成立,所以f(x)min=loga(8-2a)>1,故11恒成立,所以f(x)min=loga(8-a)>1,且8-2a>0,∴a>4,且a<4,故这样的a不存在.
综上可知,实数a的取值范围是.
考点十八 函数与方程
1.C 由题意可知f(x)的定义域为(0,+∞).在同一直角坐标系中画出函数y1=|x-2|(x>0),y2=ln x(x>0)的图象,如图所示:
由图可知函数f(x)在定义域内的零点个数为2.
2.B 当a=0时, f(x)=1,与x轴无交点,不合题意,所以a≠0,函数f(x)=3ax+1-2a在区间(-1,1)内是单调函数,又因为f(x)=3ax+1-2a在区间(-1,1)内存在一个零点,所以f(-1)·f(1)<0,即(5a-1)(a+1)>0,解得a<-1或a>,选B.
3.C 函数f(x)=的图象如图所示,
作出直线l:y=a-x,向左平移直线l,观察可得函数y=f(x)的图象与直线l:y=-x+a有两个交点,
则方程f(x)=-x+a有且只有两个不相等的实数根时,
a<1,故选C.
4.答案 5
解析 由题意知函数h(x)的图象如图所示,易知函数h(x)的图象关于直线y=x对称,函数F(x)所有零点的和就是函数y=h(x)与函数y=5-x图象交点横坐标的和,设图象交点的横坐标分别为x1,x2,因为两函数图象的交点关于直线y=x对称,所以=5-,所以x1+x2=5.
考点十九 导数及其应用
1.B ∵f(x)=2exsin x,∴f(0)=0, f '(x)=2ex(sin x+cos x),∴f '(0)=2,∴曲线f(x)在点(0, f(0))处的切线方程为y=2x.
2.C 依题意知,y'=3x2+a,则由此解得所以2a+b=1,选C.
3.答案 5
解析 f '(x)=3x2+2ax+3,由题意知x=-3为方程3x2+2ax+3=0的根,所以3×(-3)2+2a×(-3)+3=0,解得a=5.经检验,a=5符合题意.
4.答案 (-2,0)∪(2,+∞)
解析 令g(x)=,则易知g(x)为偶数,g'(x)=,∴当x>0时,g'(x)>0,即g(x)在(0,+∞)上单调递增,∵f(x)为奇函数, f(-2)=0,∴f(2)=0,∴g(2)==0,结合偶函数g(x)=的图象知,f(x)>0的解集为(-2,0)∪(2,+∞).
5.解析 (1)f '(x)=2ax+b+1+ln x,
所以2a+b+1=3且a+b=1,
解得a=1,b=0.
(2)由(1)与题意知k<=对任意的x>2恒成立,
设h(x)=(x>2),
则h'(x)=,
令m(x)=x-4-2ln x(x>2),
则m'(x)=1-=>0,
所以函数m(x)为(2,+∞)上的增函数.
因为m(8)=4-2ln 8<4-2ln e2=4-4=0,m(10)=6-2ln 10>6-2ln e3=6-6=0,
所以函数m(x)在(8,10)上有唯一零点x0,即有x0-4-2ln x0=0成立,
故当20,
即h'(x)>0,所以函数h(x)在(2,x0)上单调递减,在(x0,+∞)上单调递增,所以h(x)min=h(x0)===,
所以k<,因为x0∈(8,10),所以∈(4,5),又k∈Z.
所以k的最大值为4.
6.解析 (1)f(x)的定义域为(0,+∞),
f '(x)=+2x-a=,
因为x=3是f(x)的极值点,
所以f '(3)==0,解得a=9,
所以f '(x)==,
所以当03时,f '(x)>0;
当
查看更多