2018-2019学年河南省南阳市高二上学期期中考试数学(理)试题(解析版)
河南省南阳市2018-2019学年高二上学期期中考试数学(理)试题
一、选择题(本大题共12小题,共60.0分)
1. 若a>b,则下列不等式中正确的是( )
A. 1a<1b B. 1b+a>1a+b C. ac2>bc2 D. a2+b2≥2ab
【答案】D
【解析】解:当a=1,b=-1时,1a<1b不成立,故A不成立;
当a=1,b=-1时,1b+a>1a+b不成立,故B 不成立;
当c=0时,ac2>bc2不成立,故C不成立;
a2+b2-2ab=(a-b)2≥0恒成立,故a2+b2≥2ab,故D成立,
故选:D.
举出反例a=1,b=-1,可判断A,B;举出反例c=0,可判断C;根据完全平方公式及不等式的基本性质,可判断判断D;
本题考查的知识点是不等式的基本性质,难度不大,属于基础题.
2. 在等比数列{an}中,a3=6,a4=18,则a1+a2等于( )
A. 43 B. 83 C. 38 D. 13
【答案】B
【解析】解:根据题意,设等比数列{an}的公比为q,
又由a3=6,a4=18,则q=a4a3=3,
则a1=a3q2=23,a2=a3q=2,
则a1+a2=2+23=83;
故选:B.
根据题意,设等比数列{an}的公比为q,结合等比数列的通项公式可得q=a4a3=3,进而可得a1与a2的值,相加即可得答案.
本题考查等比数列的通项公式,关键是求出q的值,属于基础题.
3. 不等式4-x2≥0的解集是( )
A. (-∞,-2]∪[2,+∞) B. [-2,2]
C. [2,+∞) D. (-∞,2]
【答案】B
【解析】解:根据题意,4-x2≥0⇒x2≤4⇒-2≤x≤2,
即不等式4-x2≥0的解集[-2,2];
故选:B.
根据题意,4-x2≥0⇒x2≤4,解可得x的取值范围,即可得答案.
本题考查一元二次不等式的解法,关键是掌握一元二次不等式的解法,属于基础题.
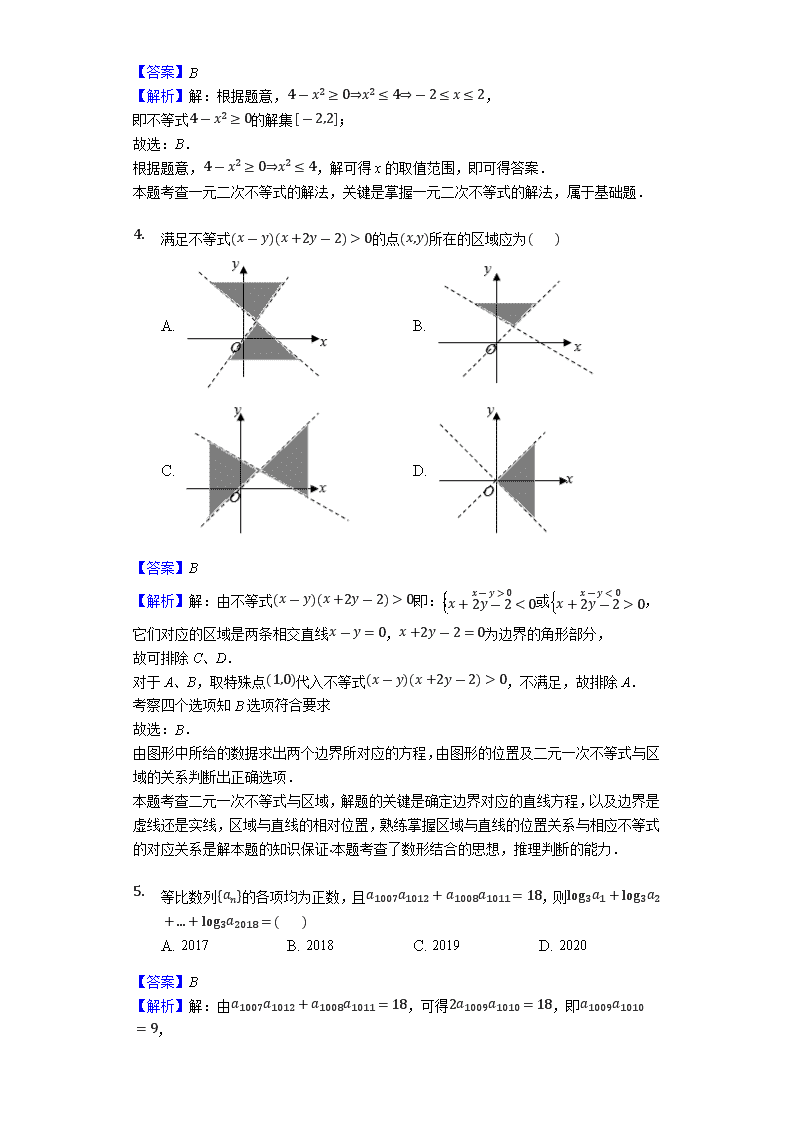
1. 满足不等式(x-y)(x+2y-2)>0的点(x,y)所在的区域应为( )
A. B.
C. D.
【答案】B
【解析】解:由不等式(x-y)(x+2y-2)>0即:x+2y-2<0x-y>0或x+2y-2>0x-y<0,
它们对应的区域是两条相交直线x-y=0,x+2y-2=0为边界的角形部分,
故可排除C、D.
对于A、B,取特殊点(1,0)代入不等式(x-y)(x+2y-2)>0,不满足,故排除A.
考察四个选项知B选项符合要求
故选:B.
由图形中所给的数据求出两个边界所对应的方程,由图形的位置及二元一次不等式与区域的关系判断出正确选项.
本题考查二元一次不等式与区域,解题的关键是确定边界对应的直线方程,以及边界是虚线还是实线,区域与直线的相对位置,熟练掌握区域与直线的位置关系与相应不等式的对应关系是解本题的知识保证.本题考查了数形结合的思想,推理判断的能力.
2. 等比数列{an}的各项均为正数,且a1007a1012+a1008a1011=18,则log3a1+log3a2+…+log3a2018=( )
A. 2017 B. 2018 C. 2019 D. 2020
【答案】B
【解析】解:由a1007a1012+a1008a1011=18,可得2a1009a1010=18,即a1009a1010=9,
∴log3a1+log3a2+…+log3a2018=log3(a1a2…a2018)
=log3(a1009a1010)1009=log391009=log332018=2018.
故选:B.
由已知结合等比数列的性质可得a1009a1010=9,再由对数的运算性质可得答案.
本题考查等比数列的性质和通项公式,涉及对数的运算,属中档题.
1. 在△ABC中,角A,B,C的边长分别为a,b,c,角A,B,C成等差数列,a=6,b=42,则此三角形解的情况是( )
A. 一解 B. 两解 C. 无解 D. 不能确定
【答案】B
【解析】解:∵角A,B,C成等差数列,
∴A+C=2B,又A+B+C=π,
∴B=π3,
∴点C到AB的距离d=asinB=33,
∵b=42,
∴d
0
∴A的取值范围是(0,π3]
故选:C.
先利用正弦定理把不等式中正弦的值转化成边,进而代入到余弦定理公式中求得cosA的范围,进而求得A的范围.
本题主要考查了正弦定理和余弦定理的应用.作为解三角形中常用的两个定理,考生应能熟练记忆.
1. 若x>0,y>0,且2x+8y-xy=0,则xy的最小值为( )
A. 8 B. 14 C. 16 D. 64
【答案】D
【解析】解:(1)∵x>0,y>0,2x+8y-xy=0,
∴xy=2x+8y≥216xy=8xy,
∴xy≥8,∴xy≥64.当且仅当x=4y=16时取等号.
故xy的最小值为64.
故选:D.
利用基本不等式构建不等式即可得出
本题考查了基本不等式的应用,属于基础题.
2. 如图是一个斜拉桥示意图的一部分,AC与BD表示两条相邻的钢缆,A、B与C、D分别表示钢缆在桥梁与主塔上的铆点,两条钢缆的仰角分别为α、β,为了便于计算,在点B处测得C的仰角为γ,若AB=m,则CD=( )
A. msinαsin(α-γ)cosβsin(β-γ) B. msinαsin(β-γ)sinβsin(α-γ)
C. mcosαsin(β-γ)cosβsin(α-γ) D. msinαsin(β-γ)cosβsin(α-γ)
【答案】D
【解析】解:在△ABC中,由正弦定理可得ABsin(α-γ)=BCsin(π-α),
∴BC=msinαsin(α-γ),
在△BCD中,由正弦定理可得BCsin(π2-β)=CDsin(β-γ),
∴CD=BCsin(β-γ)cosβ=msinαsin(β-γ)cosβsin(α-γ)
故选:D.
根据正弦定理即可求出.
本题考查了正弦定理的应用,属于基础题
1. 设变量x,y满足约束条件x+y≥1x-y≥-12x-y≤2.目标函数z=ax+2y仅在(1,0)处取得最小值,则a的取值范围为( )
A. (-1,2) B. (-2,4) C. (-4,0] D. (-4,2)
【答案】D
【解析】解:作出不等式组对应的平面区域如图:
当a=0时,显然成立.
当a>0时,直线ax+2y-z=0的斜率k=-a2>kAC=-1,
解得a<2.
当a<0时,k=-a2-4.
综合得-40,S21<0,则数列{Snan}前11项中( )
A. 首项最大 B. 第9项最大 C. 第10项最大 D. 第11项最大
【答案】C
【解析】解:等差数列{an}的前n项和为Sn,
∵S20>0,S21<0,
∴20(a1+a20)2>0,21(a1+a21)2=21a11<0,
∴a11+a10>0,a11<0,
∴a11<0,a10>0,
∴数列{Snan}中,前10项都为正数,第11项为负;
且分子Sn是递增的正数,分母an是递减的正数,
∴第10项S10a10最大.
故选:C.
根据等差数列的前n
项和的定义与计算公式得出a10>0,a11<0,
从而得出数列{Snan}中前10项都为正数,第11项为负;
且分子Sn是递增的正数,分母an是递减的正数,第10项S10a10最大.
本题考查了等差数列的前n项和公式与推理论证能力的应用问题,是中档题.
二、填空题(本大题共4小题,共20.0分)
1. 已知数列{an}的前n项和Sn=n2-1,那么a3等于______.
【答案】5
【解析】解:根据题意,数列{an}的前n项和Sn=n2-1,
则a3=S3-S2=(32-1)-(22-1)=5;
故答案为:5.
根据题意,由数列的前n项公式可得a3=S3-S2,代入数据计算可得答案.
本题考查数列的前n项和公式的应用,注意an=sn-sn-1的应用,属于基础题.
2. 点(3,1)和(-4,6)在直线3x-2y+a=0的两侧,则实数a的取值范围是______.
【答案】(-7,24)
【解析】解:由题意点(3,1)和(-4,6)在直线3x-2y+a=0的两侧
∴(3×3-2×1+a)(3×(-4)-2×6+a)<0
即(7+a)(-24+a)<0
解得-70.
【答案】解:根据题意,分3种情况讨论:
①,当a=0时,不等式即-x>0,即x<0,
此时不等式的解集为(-∞,0);
②,当a≠0时,方程ax2-x=0有2根,分别为0和1a,
当a>0时,1a>0
,此时不等式的解集为(-∞,0)∪(1a,+∞);
当a<0时,1a<0,此时不等式的解集为(1a,0);
综合可得:当a>0时,不等式的解集为(-∞,0)∪(1a,+∞);
当a=0时,不等式的解集为(-∞,0);
当a<0时,不等式的解集为(1a,0).
【解析】根据题意,分2种情况讨论a的取值范围,求出不等式的解集,综合即可得答案.
本题考查含有参数的不等式的解法,注意讨论a的取值范围,属于基础题.
1. 已知a,b,c分别是△ABC三个内角A,B,C的对边,且(2a-b)cosC=ccosB.
(1)求角C的大小;
(2)若c=2,△ABC的周长为6,求该三角形的面积.
【答案】(本题满分为12分)
解:(1)由正弦定理得2sinAcosC-sinBcosC=sinCcosB,
即2sinAcosC=sinBcosC+sinCcosB,……………………………………(2分)
即2sinAcosC=sin(B+C)=sinA,
由于sinA≠0,
故cosC=12,…………(4分)
又02).
(II)因为x>0,所以225x+3602x≥2225×3602=10800,
所以y=225x+3602x-360≥10440,当且仅当225x=3602x时,等号成立.
即当x=24m时,修建围墙的总费用最小,最小总费用是10440元.
【解析】(I)设矩形的另一边长为am,则根据围建的矩形场地的面积为360m2,易得a=360x,此时再根据旧墙的维修费用为45元/m,新墙的造价为180元/m,我们即可得到修建围墙的总费用y表示成x的函数的解析式;
(II)根据(I)中所得函数的解析式,利用基本不等式,我们易求出修建此矩形场地围墙的总费用最小值,及相应的x值.
函数的实际应用题,我们要经过析题→建模→解模→还原四个过程,在建模时要注意实际情况对自变量x取值范围的限制,解模时也要实际问题实际考虑.将实际的最大(小)化问题,利用函数模型,转化为求函数的最大(小)是最优化问题中,最常见的思路之一.
1. 设Sn是等差数列{an}的前n项和,已知a1+a3=-2,S15=75(n∈N*).
(Ⅰ)求S9;
(Ⅱ)若数列bn=1(an+4)(an+1+4),求数列{bn}的前n项和Tn.
【答案】解:(Ⅰ)设等差数列{an}的公差为d,则由a1+a3=-2,S15=75,得
15a1+105d=752a1+2d=-2,解得d=1a1=-2.
∴S9=9×(-2)+9×82×1=18;
(Ⅱ)由(Ⅰ)知,an=-2+1×(n-1)=n-3,
∴bn=1(an+4)(an+1+4)=1(n+1)(n+2)=1n+1-1n+2,
∴Tn=b1+b2+b3+…+bn=(12-13)+(13-14)+…+(1n+1-1n+2)
=12-1n+2=n2n+4.
【解析】(Ⅰ)设等差数列{an}的公差为d,由题意列关于首项和公差的方程组,求出首项和公差,则S9可求;
(Ⅱ)由(Ⅰ)求出等差数列{an}的通项,代入bn=1(an+4)(an+1+4),利用裂项相消法求数列{bn}的前n项和Tn.
本题考查等差数列的通项公式,考查了利用裂项相消法求数列的前n项和,是中档题.
1. 如图,某学校拟建一块五边形区域的“读书角”,三角形区域ABE为书籍摆放区,沿着AB、AE处摆放折线形书架(书架宽度不计),四边形区域为BCDE为阅读区,若∠BAE=60∘,∠BCD=∠CDE=120∘,DE=3BC=3CD=33m.
(1)求两区域边界BE的长度;
(2)若区域ABE为锐角三角形,求书架总长度AB+AE的取值范围.
【答案】解:(1)连接BD,在△BDC中,BC=CD=3,∠BCD=120∘,
由余弦定理BD2=BC2+CD2-2BC⋅CD⋅cos∠BCD,
得BD2=(3)2+(3)2-23⋅3cos120∘,得BD=3m,………(2分)
又BC=CD,∠BCD=120∘,
∴∠BDC=30∘,∠BDE=90∘,
△ABE中,BD=3,DE=33,由勾股定理BE2=BD2+DE2=32+(33)2=36,故BE=6m.……………(5分)
(2)设∠ABE=α,
则∠AEB=180∘-60∘-α=120∘-α,
在△ABE中,由正弦定理ABsin(120∘-α)=BEsin60∘=AEsinα=632=43,
AB=43sin(120∘-α),AE=43sinα,…………………………………(7分)
故AB+AE=43[sinα+sin(120∘-α)]=43(sinα+sin120∘cosα-cos120∘sinα)=43(32sinα+32cosα)=12sin(α+30∘),………………(9分)
△ABE为锐角三角形,
故30∘<α<90∘,60∘<α+30∘<120∘,
∴320,
∴{Sn}单调递增,
又S8=2048<4032,S9=4608>4032,
∴关于n的不等式Sn<4032的最大正整数解为8.
【解析】(1)对条件式取倒数,移项即可得出1an+1-1an=12,故而数列{1an}为等差数列,利用等差数列的通项公式求出1an即可得出an;
(2)根据不等式(12)n
查看更多