【数学】辽宁省葫芦岛市2020届高三下学期第一次模拟考试（理）

【数学】辽宁省葫芦岛市2020届高三下学期第一次模拟考试（理）

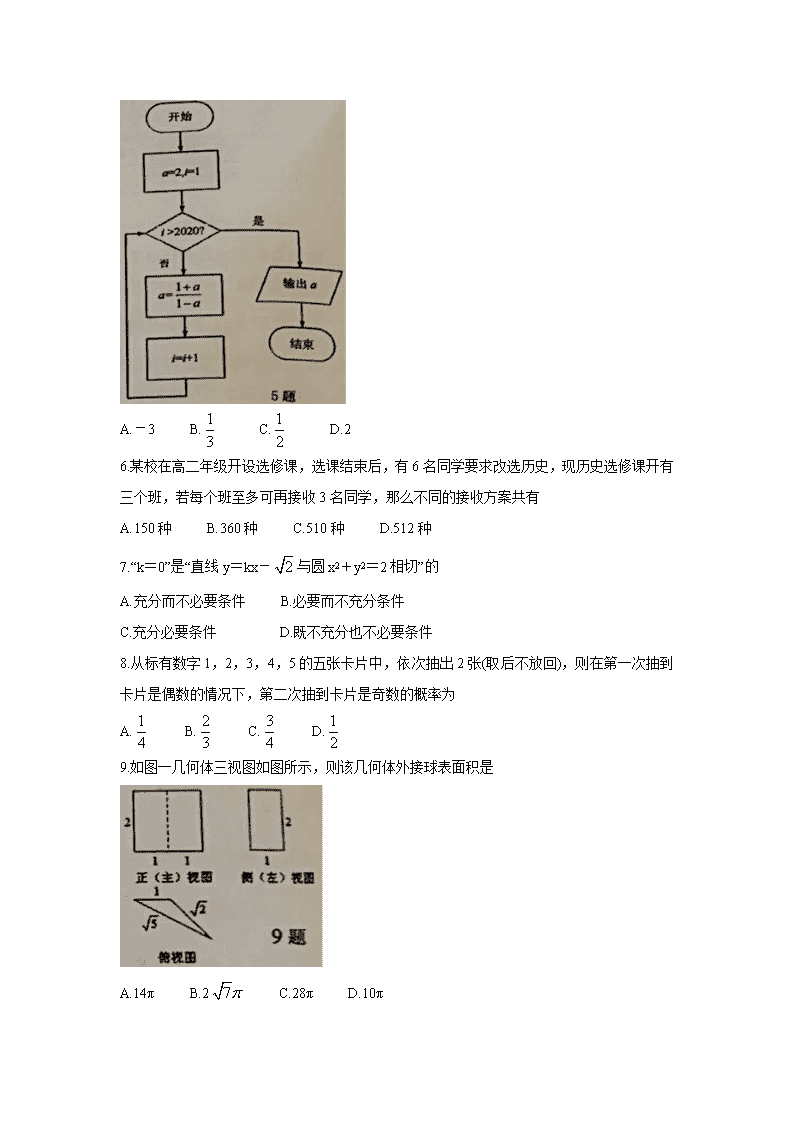
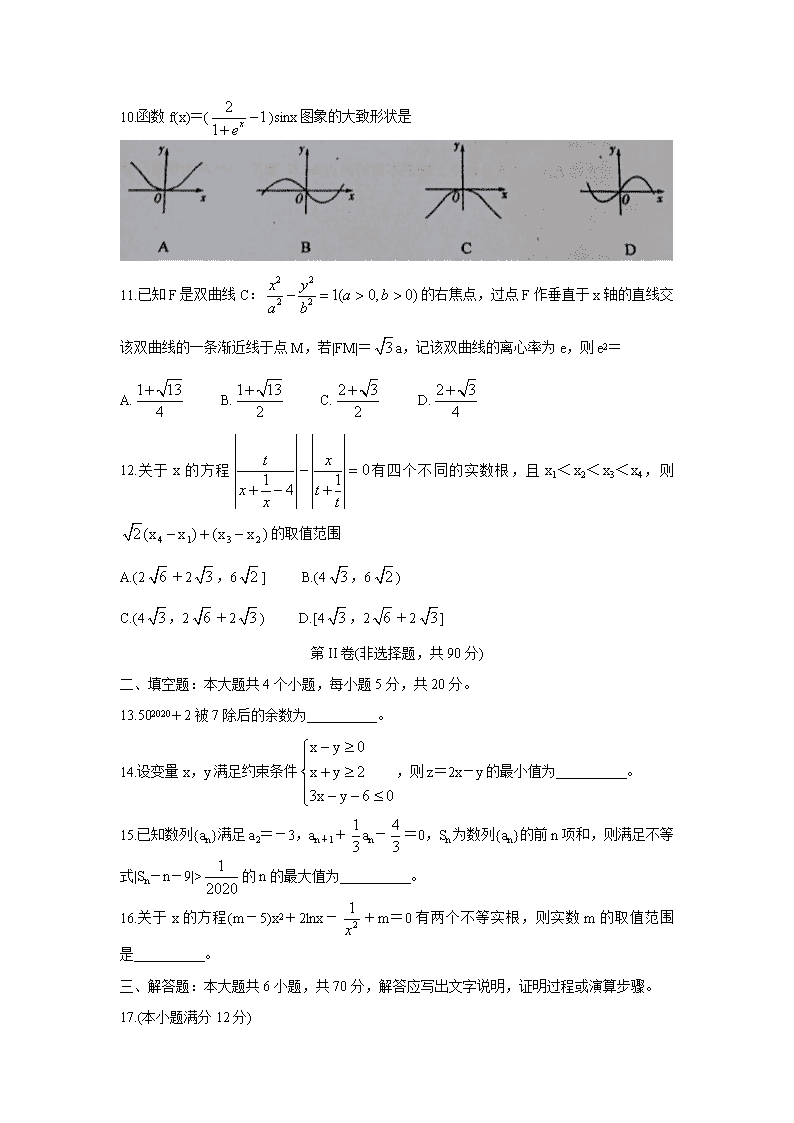
辽宁省葫芦岛市2020届高三下学期第一次模拟考试（理）‎ 注意事项：‎ ‎1.本试卷分第I卷、第II卷两部分，共6页。满分150分；考试时间：120分钟。‎ ‎2.答题前，考生务必将自己的姓名、准考证号、考试科目、试卷类型用2B铅笔涂在答题卡上。‎ ‎3.用铅笔把第I卷的答案涂在答题卡上，用钢笔或圆珠笔把第II卷的答案写在答题纸的相应位置上。‎ ‎4.考试结束，将答题卡和答题纸一并交回。‎ 第I卷(选择题，共60分)‎ 一、选择题：本题共12个小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎1.复数z满足z(1－i)＝2i，则复数z＝‎ A.1－i B.1＋2i C.1＋i D.－1＋i ‎2.设集合A＝{x|1≤x≤3}，B＝{x|x2－2x－8<0}，则A∪B＝‎ A.{x|－2＜x＜4} B.{x|1≤x＜2} C.{x|－4＜x≤3} D.{x|1≤x＜4}‎ ‎3.已知向量a＝(－2，3)，b＝(3，m)，且a//b，则m＝‎ A.－2 B.2 C.－ D.‎ ‎4.某地区甲、乙、丙、丁四所高中分别有120，150，180，150名高三学生参加某次数学调研考试。为了解学生能力水平，现制定以下两种卷面分析方案：方案①：从这600名学生的试卷中抽取一个容量为200的样本进行分析；方案②：丙校参加调研考试的学生中有30名数学培优生，从这些培优生的试卷中抽取10份试卷进行分析。完成这两种方案宜采用的抽样方法依次是 A.分层抽样法、系统抽样法 B.分层抽样法、简单随机抽样法 C.系统抽样法、分层抽样法 D.简单随机抽样法、分层抽样法 ‎5.执行如图所示的程序框图，则输出的a值为 ‎ ‎ A.－3 B. C. D.2‎ ‎6.某校在高二年级开设选修课，选课结束后，有6名同学要求改选历史，现历史选修课开有三个班，若每个班至多可再接收3名同学，那么不同的接收方案共有 A.150种 B.360种 C.510种 D.512种 ‎7.“k＝0”是“直线y＝kx－与圆x2＋y2＝2相切”的 A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件 ‎8.从标有数字1，2，3，4，5的五张卡片中，依次抽出2张(取后不放回)，则在第一次抽到卡片是偶数的情况下，第二次抽到卡片是奇数的概率为 A. B. C. D. ‎ ‎9.如图一几何体三视图如图所示，则该几何体外接球表面积是 A.14π B.2 C.28π D.10π ‎10.函数f(x)＝()sinx图象的大致形状是 ‎11.已知F是双曲线C：的右焦点，过点F作垂直于x轴的直线交该双曲线的一条渐近线于点M，若|FM|＝a，记该双曲线的离心率为e，则e2＝‎ A. B. C. D.‎ ‎12.关于x的方程有四个不同的实数根，且x1＜x2＜x3＜x4，则的取值范围 A.(2＋2，6] B.(4，6)‎ C.(4，2＋2) D.[4，2＋2]‎ 第II卷(非选择题，共90分)‎ 二、填空题：本大题共4个小题，每小题5分，共20分。‎ ‎13.502020＋2被7除后的余数为 。‎ ‎14.设变量x，y满足约束条件，则z＝2x－y的最小值为 。‎ ‎15.已知数列{an}满足a2＝－3，an＋1＋an－＝0，Sn为数列{an}的前n项和，则满足不等式|Sn－n－9|>的n的最大值为 。‎ ‎16.关于x的方程(m－5)x2＋2lnx－＋m＝0有两个不等实根，则实数m的取值范围是 。‎ 三、解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤。‎ ‎17.(本小题满分12分)‎ 已知函数f(x)＝sinx·cos(x－)－(x∈R)。‎ ‎(1)求f()的值和f(x)的最小正周期；‎ ‎(2)设锐角△ABC的三边a，b，c所对的角分别为A，B，C，且f()＝，a＝2，求b＋c的取值范围。‎ ‎18.(本小题满分12分)‎ 如图，在三棱柱ABC－A1B1C1中，BB1⊥平面ABC，AB⊥BC，AA1＝AB＝BC＝2。‎ ‎ ‎ ‎(1)求证：BC1平面A1B1C；‎ ‎(2)求异面直线B1C与A1B所成角的大小；‎ ‎(3)点M在线段BC上，且＝λ(λ∈(0，1)，点N在线段A1B上，若MN//平面A1ACC1，求的值(用含λ的代数式表示)。‎ ‎19.(本小题满分12分)‎ ‎2020年是具有里程碑意义的一年，我们将全面建成小康社会，实现第一个百年奋斗目标；2020年也是脱贫攻坚决战决胜之年。(总书记二〇二〇年新年贺词)截至2018年底，中国农村贫困人口从2012年的9899万人减少至1660万人，贫困发生率由2012年的10。2%下降至2018年的1。7%；连续7年每年减贫规模都在1000万人以上；确保到2020年农村贫困人口实现脱贫，是我们党立下的军令状，脱贫攻坚越到最后时刻，越要响鼓重锤。某贫困地区截至2018年底，按照农村家庭人均年纯收入8000元的小康标准，该地区仅剩部分家庭尚未实现小康。现从这些尚未实现小康的家庭中随机抽取50户，得到这50户家庭2018年的家庭人均年纯收入的频率分布直方图。‎ ‎(1)将家庭人均纯年收入不足5000元的家庭称为“特困户”，若从这50户家族中再取出10户调查致贫原因，求这10户中含有“特困户”的户数X的数学期望；‎ ‎(2)2019年7月，为估计该地能否在2020年全面实现小康，统计了该地当时最贫困的一个家庭2019年1至6月的人均月纯收入如下表：‎ 由散点图及相关性分析发现：家庭人均月纯收入y与时间代码x之间具有较强的线任相关关系，由此估计该家庭2020年能实现小康生活，但2020年1月突如其来的新冠肺次疫情影响了奔小康的进展，该家庭2020年第一季度(1，2，3月份)每月的人均月纯收入均只有2019年12月的预估值的，为加快脱贫进程，政府加大扶贫力度，拟从2020年3月份起，以后每月的增长率为a，为了使2020年该家庭顺利迈入小康生活，则a至少应为多少?(保留小数点后两位数字)；‎ ‎①可能用到的数据：‎ ‎②参考公式：线性回归方程中，。‎ ‎20.(本小题满分12分)‎ 已知椭圆C：离心率是，F1，F2分别是椭圆C的左、右焦点，过F2作斜率为k的直线l，交椭圆C于A，B两点，且三角形△F1AB周长4。‎ ‎(1)求椭圆C的标准方程；‎ ‎(2)若直线F1A，F1B分别交y轴于不同的两点M，N。如果∠MF1N为锐角，求k的取值范围。‎ ‎21.(本小题满分12分)‎ 已知函数f(x)＝mex(x＋1)(m≠0)；g(x)＝lnx－ax－a2－3a＋1。‎ ‎(1)若f(x)在(0，m)处的切线的方程为y＝－8x－4，求此时f(x)的最值；‎ ‎(2)若对任意x∈[1，＋∞)，a∈[－1，0)，不等式g(x)>f(a)恒成立，求实数m的取值范围。‎ 请考生在第22、23题中任选一题做答，如果多做，则按所做的第一题记分。做答时请写清题号。‎ ‎22.(本小题满分10分)选修4—4：坐标系与参数方程 在直角坐标系xOy中，曲线C的参数方程为(其中α为参数)，曲线C2‎ 的参数方程为(其中α为参数)，以原点O为极点，x轴的正半轴为极轴建立极坐标系。‎ ‎(1)求曲线C1，C2的极坐标方程；‎ ‎(2)射线l：θ＝ρ(ρ≥0)与曲线C1，C2分别交于点A，B(且点A，B均异于原点O)，当0<φ≤时，求|OA|2＋|OB|2的最小值。‎ ‎23.(本小题满分10分)选修4－5：不等式选讲 已知函数f(x)＝|x|－|2x－2|。‎ ‎(1)求不等式f(x)≥－3的解集；‎ ‎(2)若a∈R，且a≠0，证明：|4a－1|＋|＋1|≥4f(x)。‎ 参考答案 第I卷（选择题)‎ 一、选择题（本小题共12小题，每小题5分，共60分，在每个小题给出的四个选项中，只有一项是符合题目要求）‎ ‎1．D 2．A 3．C 4．B 5．D 6．C 7．C 8．C 9．A 10．C 11．B 12．B 第II卷（非选择题)‎ 二、填空题(本题共4个小题，每小题5分，共20分)‎ ‎13．3 14．1 15．8 16．‎ 三、解答应写出文字说明、证明过程或演算步骤。第17－21题为必考题，每个试题考生都必须作答。第22、23题为选考题，考生根据要求作答。‎ ‎(一)必考题，共60分。‎ ‎17．(本小题满分12分)‎ 由题 ‎.--------------------------4‎ ‎（1）,.--------------6‎ ‎（2）,,所以,---------------8‎ 在中,由余弦定理可得：‎ ‎,即,-------------------10‎ 又因为在中,,‎ 所以,综上可得：的取值范围是.--------------------------------------12‎ 18． ‎(本小题满分12分)‎ ‎（1）在三棱柱中，由平面，所以平面，‎ 又因为平面，所以平面平面，交线为.‎ 又因为，所以，所以平面.‎ 因为平面，所以 又因为，所以，‎ 又，所以平面.-----------------------------4‎ ‎（2）由（1）知底面，，如图建立空间直角坐标系，‎ 由题意得，，，.‎ 所以，.‎ 所以.‎ 故异面直线与所成角的大小为.---------------------------8‎ ‎（3）易知平面的一个法向量，‎ 由，得.‎ 设，得，则 因为平面，所以，‎ 即，解得，所以.-----------------------------12‎ ‎19．(本小题满分12分)[来源 ‎（1）解：由频率分布直方图可知，‎ 家庭人均年收入在[2000,3000)元的家庭数为:0.04´50=2户;‎ 家庭人均年收入在[3000,4000)元的家庭数为:0.10´50=5户;‎ 家庭人均年收入在[4000,5000)元的家庭数为:0.32´50=16户;‎ 家庭人均年收入在[5000,6000)元的家庭数为:0.30´50=15户;‎ 家庭人均年收入在[6000,7000)元的家庭数为:0.18´50=9户;‎ 家庭人均年收入在[7000,8000)元的家庭数为:0.06´50=3户;‎ 共计50户,其中家庭人均年收入不足5000元的特困户有:2+5+16=23户;----------------2‎ 由题意:X满足参数为50,23,10的超几何分布,所以EX=10´=4.6户；‎ 即这10户中含有“特困户”的户数X的数学期望为4.6（户）；---------------4‎ ‎（2）解：由题意得：==3.5,===410‎ xi2=1+4+9+16+25+36=91 6´2=6´3.52=73.5‎ 所以：=====40‎ =-=410-40´3.5=270‎ 所以回归直线方程为：=40x+270------------------------------6‎ 令x=12,则可知2019年12月份该家庭人均月纯收入为40 x12+270=750（元）‎ 由此可知2020年第一季度（1月份，2月份，3月份）该家庭人均月纯收入为750 x=500（元）‎ ‎∵从2020年3月份起，每月的增长率为a,设从开始3月份到12月份的月纯收入之和为S10‎ ‎,则S10=500+500 x(1+a)+500 x(1+a)2+…+500 x(1+a)9== 由题意应有：∴500+500+≥8000 ‎ 即： ≥14----------------------------8‎ 显然S10是以a为自变量的增函数，∴是以a为自变量的增函数 ①当a≥0.15时，≥≈=20>14 显然成立---------------10‎ ②当00得：x<-2, 由f¢(x)<0得：x>-2‎ ‎∴f(x)在(-∞,-2)上单调递增；在(-2,+∞)上单调递减 ‎∴fmax(x)=f(-2)=,无最小值；‎ ‎(2) g(x)>f(a)Û lnx-ax-a2-3a+1> mea(a+1) Û lnx-ax> mea(a+1) +a2+3a-1‎ Û(lnx-ax)min> mea(a+1) +a2+3a-1‎ 令φ(x)= lnx-ax ∵a∈[-1,0) ∴φ(x)= lnx-ax在[1,+∞)上单调递增 φmin(x)=φ(1)=-a ‎∴(lnx-ax)min> mea(a+1) +a2+3a-1Û-a> mea(a+1) +a2+3a-1Û mea(a+1) +a2+4a-1<0‎ 令h(a)= mea(a+1) +a2+4a-1, a∈[-1,0) h¢(a)=mea(a+2) +2a+4=(a+2)(mea+2)=ea(a+2)(+m)‎ ‎∵a∈[-1,0) ∴∈(2,2e]‎ ① 当-m£2即m≥-2时，h¢(a)>0,∴h(a)在[-1,0)上单调递增，若使h(a)<0恒成立，只需h(0)£0‎ m£1 ∴m∈[-2,0)∪(0,1]‎ ‎②当-m≥2e即m£-2e时, h¢(a)£0 ∴h(a)在[-1,0)上单调递减，若使h(a)<0恒成立，只需h(-1)£0 即-4<0 m£-2e合题意；‎ ① 当2<-m<2e即-2e0得：-1 令t(a)= 则t¢(a)=- ‎∵a∈(-1,0) ∴t¢(a)>0 t(a)在(-1,0)上单调递增 由题意：-m£t(0)=-1 即m£1 又∵m≠0‎ ‎∴m的取值范围为(-∞,0)∪(0,1]‎ ‎ (二)选考题：共10分。请考生在22、23题中任选一题作答，如果多做，则按所做的第一题记分。‎ ‎22．(本小题满分10分)选修4—4：坐标系与参数方程 ‎（1）曲线的普通方程为，令，，‎ 可得的极坐标方程为，‎ 曲线的普通方程为，令，，‎ 可得的极坐标方程为.---------------------5‎ ‎（2）联立与的极坐标方程得，‎ 联立与的极坐标方程得，‎ 则 ‎（当且仅当时取等号）.‎ 所以的最小值为.-------------------------10‎ ‎23．(本小题满分10分)选修4—5：不等式选讲 ‎(1)法一：‎ ‎，‎ 作出的图象，如图所示：‎ 结合图象，‎ 函数上单调递增，‎ 在上单调递减，‎ 又，，‎ 所以不等式的解集是.------------------------5‎ 法二：，‎ 等价于：或或，‎ 解得：或或，‎ 所以不等式的解集是.----------------5‎ ‎(2)由(1)知函数的最大值是，所以恒成立.‎ 因为，‎ 当且仅当时，等号成立.‎ 所以.--------------------------10‎