高考数学【理科】真题分类详细解析版专题10 圆锥曲线(原卷版)
专题 10 圆锥曲线
【2013 高考真题】
(2013·新课标 I 理)10、已知椭圆x2
a2+y2
b2=1(a>b>0)的右焦点为 F(3,0),过点 F 的直
线交椭圆于 A、B 两点。若 AB 的中点坐标为(1,-1),则 E 的方程为 ( )
A、x2
45+y2
36=1 B、x2
36+y2
27=1 C、x2
27+y2
18=1 D、x2
18+y2
9=1
(2013·上海理)9.设 AB 是椭圆 的长轴,点 C 在 上,且 ,若
AB=4,
,则 的两个焦点之间的距离为________
(2013·辽宁理)(15)已知椭圆 的左焦点为
.
(2013·福建理)14. 椭圆 的左右焦点分别为 ,焦距为 ,
若直线 与椭圆的一个交点满足 ,则该椭圆的离心率等于
_____
(2013·大纲理)8.椭圆 C: 的左右顶点分别为 ,点 P 在 C 上且直线
斜率的取值范围是 ,那么直线 斜率的取值范围是( )
A. B. C. D.
Γ Γ
4CBA
π∠ =
2BC = Γ
2 2
2 2: 1( 0)x yC a ba b
+ = > >
,F C与过原点的直线相交于 ,A B两点,
4, . 10, 6,cos ABF ,5AF BF AB AF C e= = ∠ =连接 若 则 的离心率 =
( )01: 2
2
2
2
>>=+Γ bab
y
a
x
21, FF c2
( )cxy += 3 1221 2 FMFFMF ∠=∠
2 2
14 3
x y+ = 1 2,A A
2PA [ 2, 1]− − 1PA
1 3[ , ]2 4
3 3[ , ]8 4
1[ ,1]2
3[ ,1]4
(2013·北京理)19. (本小题共 14 分)
已知 A、B、C 是椭圆 W: 上的三个点,O 是坐标原点.
(I)当点 B 是 W 的右顶点,且四边形 OABC 为菱形时,求此菱形的面积.
(II)当点 B 不是 W 的顶点时,判断四边形 OABC 是否可能为菱形,并说明理由.
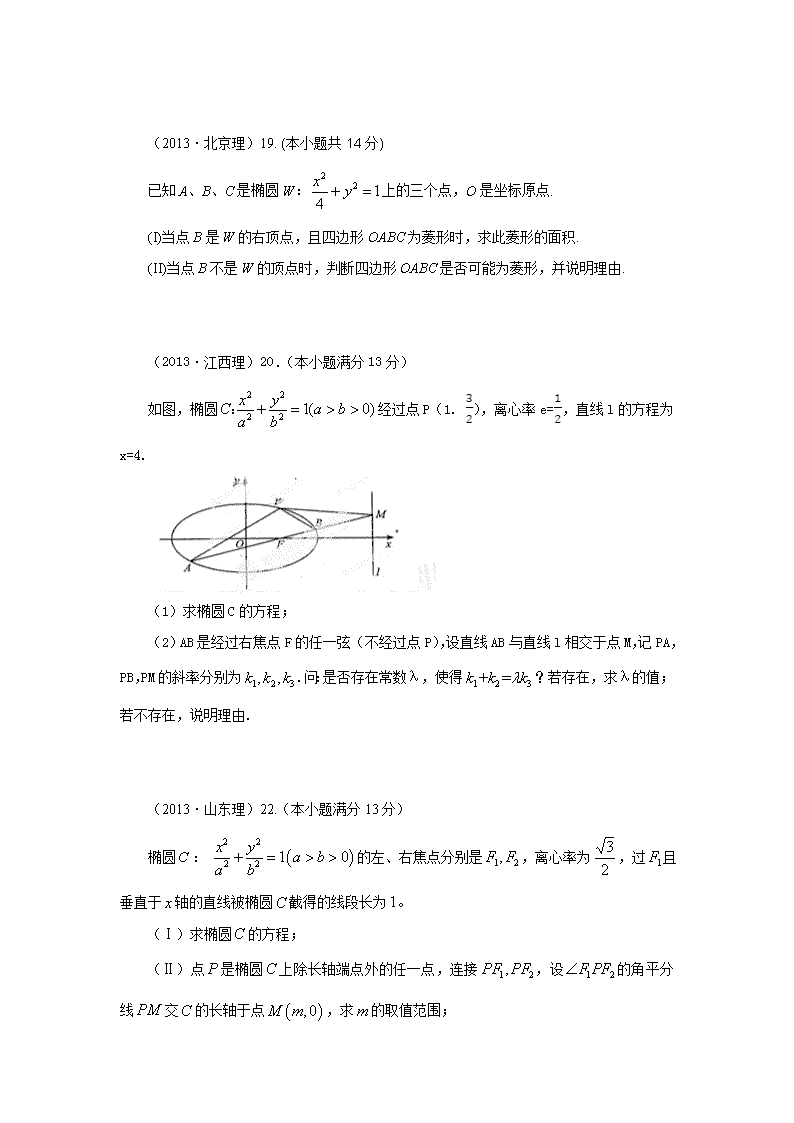
(2013·江西理)20.(本小题满分 13 分)
如图,椭圆 经过点 P(1. ),离心率 e= ,直线 l 的方程为
x=4.
(1)求椭圆 C 的方程;
(2)AB 是经过右焦点 F 的任一弦(不经过点 P),设直线 AB 与直线 l 相交于点 M,记
PA,PB,PM 的斜率分别为 .问:是否存在常数λ,使得 ?若存在,求λ
的值;若不存在,说明理由.
(2013·山东理)22.(本小题满分 13 分)
椭圆 : 的左、右焦点分别是 ,离心率为 ,过 且
垂直于 轴的直线被椭圆 截得的线段长为 。
(Ⅰ)求椭圆 的方程;
(Ⅱ)点 是椭圆 上除长轴端点外的任一点,连接 ,设 的角平分
线 交 的长轴于点 ,求 的取值范围;
2
2 14
x y+ =
2 2
2 2 1( 0)x yC a ba b
+ = > >:
1 2 3, ,k k k 1 2 3+ =k k kλ
C ( )2 2
2 2 1 0x y a ba b
+ = > > 1 2,F F 2
3
1F
x C 1
C
P C 1 2,PF PF 1 2F PF∠
PM C ( ),0M m m
(Ⅲ)在(Ⅱ)的条件下,过点 作斜率为 的直线 ,使 与椭圆 有且只有一个公
共点,设直线的 斜率分别为 。若 ,试证明 为定值,并求出这
个定值。
(2013·浙江理)9.如图, 是椭圆 与双曲线 的公共焦点,
分别是 , 在第二、四象限的公共点。若四边形 为矩形,则 的离心率
是( )
A. B. C. D.
(2013·浙江理)21.如图,点 是椭圆 的一个顶点,
的长轴是圆 的直径. 是过点 且互相垂直的两条直线,其中 交圆
于两点, 交椭圆 于另一点
(Ⅰ)求椭圆 的方程;
(Ⅱ)求 面积取最大值时直线 的方程.
P k l l C
1 2,PF PF 1 2,k k 0k ≠
1 2
1 1
kk kk
+
21, FF 14: 2
2
1 =+ yxC 2C
BA, 1C 2C 21BFAF 2C
2 3 2
3
2
6
)1,0( −P )0(1: 2
2
2
2
1 >>=+ bab
y
a
xC
1C 4: 22
2 =+ yxC 21,ll P 1l
2C 2l 1C D
1C
ABD∆ 1l
(2013·新课标Ⅱ理) (20)(本小题满分 12 分)
平 面 直 角 坐 标 系 xOy 中 , 过 椭 圆 M : 右 焦 点 的 直 线
交 于 A,B 两点,P 为 AB 的中点,且 OP 的斜率为 .
(Ι)求 M 的方程;
(Ⅱ)C,D 为 M 上的两点,若四边形 ACBD 的对角线 CD⊥AB,求四边形面积的最大值
(2013·新课标 I 理)(20)(本小题满分 12 分)
已知圆 M:(x+1)2+y2=1,圆 N:(x-1)2+y2=9,动圆 P 与圆 M 外切并与圆 N 内切,圆心 P
的轨迹
为曲线 C
(Ⅰ)求 C 的方程;
(Ⅱ)l 是与圆 P,圆 M 都相切的一条直线,l 与曲线 C 交于 A,B 两点,当圆 P 的半
径最长时,求|AB|.
(2013·新课标 I 理)4、已知双曲线 C:x2
a2-y2
b2=1(a>0,b>0)的离心率为 5
2 ,则 C 的渐
近线方程为 ( )
A、y=±1
4x (B)y=±1
3x (C)y=±1
2x (D)y=±x
( 2013 · 天 津 理 ) 5. 已 知 双 曲 线 的 两 条 渐 近 线 与 抛 物 线
的准线分别交于 A, B 两点, O 为坐标原点. 若双曲线的离心率为 2, △AOB 的
面积为 , 则 p = ( )
(A) 1 (B) (C) 2 (D) 3
(2013·陕西理)10. 设[x]表示不大于 x 的最大整数, 则对任意实数 x, y, 有 ( )
2 2
2 2 1( 0)x y a ba b
+ = > >
3 0x y+ − = M
1
2
2 2
2 2 1( 0, 0)x y a ba b
− = > >
2 2 ( 0)px py = >
3
3
2
(A) [-x] = -[x] (B) [2x] = 2[x]
(C) [x+y]≤[x]+[y] (D) [x-y]≤[x]-[y]
(2013·湖南理)14.设 是双曲线 的两个焦点,P 是 C
上一点,若 且 的最小内角为 ,则 C 的离心率为___。
(2013·广东理)10.若曲线 在点 处的切线平行于 轴,则 ______.
(2013·广东理)7.已知中心在原点的双曲线 的右焦点为 ,离心率等于 ,在双曲
线 的方程是 ( )
A . B. C. D.
(2013·福建理)3.双曲线 的顶点到渐进线的距离等于( )
A. B. C. D.
(2013·北京理)6.若双曲线 的离心率为 ,则其渐近线方程为
A.y=±2x B.y= C. D.
(2013·安徽理)(13)已知直线 交抛物线 于 两点。若该抛物线上存在点
,使得 为直角,则 的取值范围为___________。
1 2,F F
2 2
2 2: 1( 0, 0)x yC a ba b
− = > >
21 6 ,PF PF a+ = 1 2PF F∆ 30
C ( )3,0F
3
2
C
2 2
14 5
x y− = 2 2
14 5
x y− =
2 2
12 5
x y− =
2 2
12 5
x y− =
14
2
2
=− yx
5
2
5
4
5
52
5
54
ay = 2xy = ,A B
C ACB∠ a
lny kx x= + ( )1,k x k =
2 2
2 2 1x y
a b
− = 3
2x± 1
2y x= ± 2
2y x= ±
(2013·大纲理)21.(本小题满分 12 分)
已知双曲线 C: (a>0,b>0)的左、右焦点分别为 、 ,离心率为 3,直
线 y=2 与 C 的两个交点间的距离为 .
(Ⅰ)求 a,b;
(Ⅱ)设过 的直线 l 与 C 的左、右两支分别交于 A、B 两点,且 ,证明:
、 、 成等比数列.
(2013·上海理)22.(3 分+5 分+8 分)如图,已知曲线 ,曲线
,P 是平面上一点,若存在过点 P 的直线与 都有公共点,则称 P 为
“C1—C2 型点”.
(1)在正确证明 的左焦点是“C1—C2 型点”时,要使用一条过该焦点的直线,试写
出一条这样的直线的方程(不要求验证);
(2)设直线 与 有公共点,求证 ,进而证明原点不是“C1—C2 型点”;
(3)求证:圆 内的点都不是“C1—C2 型点”.
(2013·上海理)7.在极坐标系中,曲线 与 的公共点到极点的距
离为__________
2 2
2 2 1x y
a b
− = 1F 2F
6
2F 1 1| | | |AF BF=
2| |AF | |AB 2| |BF
2
2
1 : 12
xC y− =
2 :| | | | 1C y x= + 1 2,C C
1C
y kx= 2C | | 1k >
2 2 1
2x y+ =
cos 1ρ θ= + cos 1ρ θ =
(2013·山东理)11.抛物线 : (p>0)的焦点与双曲线 : 的右
焦点的连线交 于第一象限的点 。若 在点 处的切线平行于 的一条渐近线。则
A. B. C. D.
(2013·江西理)14.抛物线 x2=2py(p>0)的焦点为 F,其准线与双曲线 - =1 相交
于 A,B 两点,若△ABF 为等边三角形,则 p=___________.
(2013·大纲理)11.已知抛物线 C: 与点 M(-2,2),过 C 的焦点且斜率为 k 的直
线与 C 交于 A,B 两点,若 ,则 k=( )
A. B. C. D.2
(2013·新课标Ⅱ理)(11)设抛物线 的焦点为 F,点 M 在 C 上,|MF|=5,
若以 MF 为直径的圆过点(0,2),则 C 的方程为
(A) 或 (B) 或
(C) 或 (D) 或
(2013·北京理)7.直线 l 过抛物线 C: x2=4y 的焦点且与 y 轴垂直,则 l 与 C 所围成的
图形的面积等于( )
A. B.2 C. D.
1C 2
2
1 xpy = 2C 13
2
2
=− yx
1C M 1C M 2C
p =
16
3
8
3 2 3
3 3
34
2 8y x=
0MA MB• =
1
2
2
2 2
2 2 ( 0)y px p= >
2 4y x= 2 8y x= 2 2y x= 2 8y x=
2 4y x= 2 16y x= 2 2y x= 2 16y x=
4
3
8
3
16 2
3
(2013·浙江理)15、设 为抛物线 的焦点,过点 的直线 交抛
物线 于两点 ,点 为线段 的中点,若 ,则直线的斜率等于________。
(2013·福建理)18.(本小题满分 13 分)
如图,在正方形 中, 为坐标原点,点 的坐标为 ,点 的坐标为
,分别将线段 和 十等分,分点分别记为 和 ,连接 ,
过 作 轴的垂线与 交于点 。
(1)求证:点 都在同一条抛物线上,并求抛物线 的方程;
(2)过点 作直线 与抛物线 E 交于不同的两点 , 若 与 的面积之
比为 4:1,求直线 的方程。
(2013·广东理)20.(本小题满分 14 分)
已知抛物线 的顶点为原点,其焦点 到直线 : 的距离为
.设 为直线 上的点,过点 作抛物线 的两条切线 ,其中 为切点.
F xyC 4: 2 = )0,1(−P l
C BA, Q AB 2|| =FQ
OABC O A ( )0,10 C
( )10,0 OA AB 921 ,,, AAA ⋅⋅⋅ 921 ,,, BBB ⋅⋅⋅ iOB
iA x iOB ( )91*, ≤≤∈ iNiPi
( )91*, ≤≤∈ iNiPi E
C l NM , OCM∆ OCN∆
l
C ( )( )0, 0F c c > l 2 0x y− − =
3 2
2 P l P C ,PA PB ,A B
(Ⅰ) 求抛物线 的方程;
(Ⅱ) 当点 为直线 上的定点时,求直线 的方程;
(Ⅲ) 当点 在直线 上移动时,求 的最小值.
(2013·湖南理)21.(本小题满分 13 分)
过抛物线 的焦点 F 作斜率分别为 的两条不同的直线 ,且
, 相交于点 A,B, 相交于点 C,D。以 AB,CD 为直径的圆 M,
圆 N(M,N 为圆心)的公共弦所在的直线记为 。
(I)若 ,证明; ;
(II)若点 M 到直线 的距离的最小值为 ,求抛物线 E 的方程。
(2013·辽宁理)20.(本小题满分 12 分)
如图,抛物线
(I) ;
(II)
C
( )0 0,P x y l AB
P l AF BF⋅
2: 2 ( 0)E x py p= > 1 2,k k 1 2,l l
1 2 2k k+ = 1l E与 2l E与
l
1 20, 0k k> > 22FM FN P<
l 7 5
5
( ) ( )2 2
1 2 0 0 2: 4 , : 2 0 . ,C x y C x py p M x y C= = − > 点 在抛物线 上,
1M C过 作 ( ) 0, , . 1 2A B M O A B O x = −的切线,切点为 为原点 时, 重合于 当 时,
1 .2MA切线 的斜率为-
求p的值
2M C AB N当 在 上运动时,求线段 中点 的轨迹方程
【2012 高考真题】
1.(2012·江苏卷) 在平面直角坐标系 xOy 中,若双曲线x2
m- y2
m2+4=1 的离心率为 5,
则 m 的值为________.
2.(2012·湖南卷) 已知双曲线 C:x2
a2-y2
b2=1 的焦距为 10,点 P(2,1)在 C 的渐近线上,
则 C 的方程为( )
3.(2012·全国卷) 已知 F1、F2 为双曲线 C:x2-y2=2 的左、右焦点,点 P 在 C 上,
|PF1|=2|PF2|,则 cos∠F1PF2=( )
A.1
4 B.3
5
C.3
4 D.4
5
4.(2012·课标全国卷) 等轴双曲线 C 的中心在原点,焦点在 x 轴上,C 与抛物线 y2=
16x 的准线交于 A,B 两点,|AB|=4 3,则 C 的实轴长为( )
A. 2 B.2 2 C.4 D.8
5.(2012·上海卷) 在平面直角坐标系 xOy 中,已知双曲线 C1:2x2-y2=1.
(1)过 C1 的左顶点引 C1 的一条渐近线的平行线,求该直线与另一条渐近线及 x 轴围成的
( ), , .A B O O重合于 时 中点为
三角形的面积;
(2)设斜率为 1 的直线 l 交 C1 于 P、Q 两点.若 l 与圆 x2+y2=1 相切,求证:OP⊥OQ;
(3)设椭圆 C2:4x2+y2=1,若 M、N 分别是 C1、C2 上的动点,且 OM⊥ON,求证:O
到直线 MN 的距离是定值.
6.(2012·湖北卷) 如图 1-5 所示,双曲线x2
a2-y2
b2=1(a,b>0)的两顶点为 A1,A2,虚
轴两端点为 B1,B2,两焦点为 F1,F2.若以 A1A2 为直径的圆内切于菱形 F1B1F2B2,切点分别
为 A,B,C,D.则
(1)双曲线的离心率 e=________;
(2)菱形 F1B1F2B2 的面积 S1 与矩形 ABCD 的面积 S2 的比值S1
S2=________.
图 1-5
7.(2012·四川卷) 已知抛物线关于 x 轴对称,它的顶点在坐标原点 O,并且经过点 M(2,
y0),若点 M 到该抛物线焦点的距离为 3,则|OM|=( )
A.2 2 B.2 3
C.4 D.2 5
8.(2012·陕西卷) 图 1-4 是抛物线形拱桥,当水面在 l 时,拱顶离水面 2 米,水面
宽 4 米,水位下降 1 米后,水面宽________米.
图 1-4
9.(2012·安徽卷) 过抛物线 y2=4x 的焦点 F 的直线交该抛物线于 A,B 两点,O 为坐
标原点.若|AF|=3,则△AOB 的面积为( )
A.
2
2 B. 2 C.3 2
2 D.2 2
10.(2012·浙江卷) 定义:曲线 C 上的点到直线 l 的距离的最小值称为曲线 C 到直线 l
的距离.已知曲线 C1:y=x2+a 到直线 l:y=x 的距离等于曲线 C2:x2+(y+4)2=2 到直线
l:y=x 的距离,则实数 a=________.
11.(2012·山东卷) 在平面直角坐标系 xOy 中,F 是抛物线 C:x2=2py(p>0)的焦点,
M 是抛物线 C 上位于第一象限内的任意一点,过 M,F,O 三点的圆的圆心为 Q,点 Q 到
抛物 C 的准线的距离为3
4.
(1)求抛物线 C 的方程;
(2)是否存在点 M,使得直线 MQ 与抛物线 C 相切于点 M?若存在,求出点 M 的坐标;
若不存在,说明理由;
(3)若点 M 的横坐标为 2,直线 l2:y=kx+1
4与抛物线 C 有两个不同的交点 A,B,l 与
圆 Q 有两个不同的交点 D,E,求当1
2≤k≤2 时,|AB|2+|DE|2 的最小值.
12.(2012·课标全国卷)等轴双曲线 C 的中心在原点,焦点在 x 轴上,C 与抛物线 y2=
16x 的准线交于 A,B 两点,|AB|=4 3,则 C 的实轴长为( )
A. 2 B.2 2 C.4 D.8
13.(2012·全国卷)已知抛物线 C:y=(x+1)2 与圆 M:(x-1)2+(y-1
2 )2=r2(r>0)有一
个公共点 A,且在 A 处两曲线的切线为同一直线 l.
(1)求 r;
(2)设 m、n 是异于 l 且与 C 及 M 都相切的两条直线,m、n 的交点为 D,求 D 到 l 的距
离.
14.(2012·湖南卷)在直角坐标系 xOy 中,曲线 C 1 上的点均在圆 C2:(x-5)2+y2=9
外,且对 C1 上任意一点 M,M 到直线 x=-2 的距离等于该点与圆 C 2 上点的距离的最小
值.
(1)求曲线 C1 的方程;
(2)设 P(x0,y0)(y0≠±3)为圆 C2 外一点,过 P 作圆 C2 的两条切线,分别与曲线 C1 相交于
点 A,B 和 C,D.证明:当 P 在直线 x=-4 上运动时,四点 A,B,C,D 的纵坐标之积为
定值.
15.(2012·北京卷)在直角坐标系 xOy 中,直线 l 过抛物线 y2=4x 的焦点 F,且与该抛
物线相交于 A,B 两点,其中点 A 在 x 轴上方,若直线 l 的倾斜角为 60°,则△OAF 的面积
为________.
.
16.(2012·课标全国卷)设抛物线 C:x2=2py(p>0)的焦点为 F,准线为 l,A 为 C 上一
点,已知以 F 为圆心,FA 为半径的圆 F 交 l 于 B,D 两点.
(1)若∠BFD=90°,△ABD 的面积为 4 2,求 p 的值及圆 F 的方程;
(2)若 A、B、F 三点在同一直线 m 上,直线 n 与 m 平行,且 n 与 C 只有一个公共点,
求坐标原点到 m,n 距离的比值.
17.(2012·重庆卷)过抛物线 y2=2x 的焦点 F 作直线交抛物线于 A、B 两点,若|AB|=25
12,
|AF|<|BF|,则|AF|=________.
18.(2012·重庆卷)如图 1-3,设椭圆的中心为原点 O,长轴在 x 轴上,上顶点为 A,
左、右焦点分别为 F1,F2,线段 OF1,OF2 的中点分别为 B1,B2,且△AB1B2 是面积为 4 的
直角三角形.
图 1-3
(1)求该椭圆的离心率和标准方程;
(2)过 B1 作直线 l 交椭圆于 P,Q 两点,使 PB2⊥QB2,求直线 l 的方程.
19.(2012·天津卷)设椭圆x2
a2+y2
b2=1(a>b>0)的左、右顶点分别为 A,B,点 P 在椭圆
上且异于 A,B 两点,O 为坐标原点.
(1)若直线 AP 与 BP 的斜率之积为-1
2,求椭圆的离心率;
(2)若|AP|=|OA|,证明直线 OP 的斜率 k 满足|k|> 3.
20.(2012·山东卷)在平面直角坐标系 xOy 中,F 是抛物线 C:x2=2py(p>0)的焦点,M
是抛物线 C 上位于第一象限内的任意一点,过 M,F,O 三点的圆的圆心为 Q,点 Q 到抛物
C 的准线的距离为3
4.
(1)求抛物线 C 的方程;
(2)是否存在点 M,使得直线 MQ 与抛物线 C 相切于点 M?若存在,求出点 M 的坐标;
若不存在,说明理由;
(3)若点 M 的横坐标为 2,直线 l2:y=kx+1
4与抛物线 C 有两个不同的交点 A,B,l 与
圆 Q 有两个不同的交点 D,E,求当1
2≤k≤2 时,|AB|2+|DE|2 的最小值.
21.(2012·湖南卷)在直角坐标系 xOy 中,曲线 C1 上的点均在圆 C2:(x-5)2+y2=9
外,且对 C1 上任意一点 M,M 到直线 x=-2 的距离等于该点与圆 C 2 上点的距离的最小
值.
(1)求曲线 C1 的方程;
(2)设 P(x0,y0)(y0≠±3)为圆 C2 外一点,过 P 作圆 C2 的两条切线,分别与曲线 C1 相交于
点 A,B 和 C,D.证明:当 P 在直线 x=-4 上运动时,四点 A,B,C,D 的纵坐标之积为
定值.
22.(2012·湖北卷)设 A 是单位圆 x 2+y2=1 上的任意一点,l 是过点 A 与 x 轴垂直的直
线,D 是直线 l 与 x 轴的交点,点 M 在直线 l 上,且满足|DM|=m|DA|(m>0,且 m≠1).当点
A 在圆上运动时,记点 M 的轨迹为曲线 C.
(1)求曲线 C 的方程,判断曲线 C 为何种圆锥曲线,并求其焦点坐标;
(2)过原点且斜率为 k 的直线交曲线 C 于 P,Q 两点,其中 P 在第一象限,它在 y 轴上
的射影为点 N,直线 QN 交曲线 C 于另一点 H.是否存在 m,使得对任意的 k>0,都有
PQ⊥PH?若存在,求 m 的值;若不存在,请说明理由.
23.(2012·湖北卷)如图 1-5 所示,双曲线x2
a2-y2
b2=1(a,b>0)的两顶点为 A1,A2,虚
轴两端点为 B1,B2,两焦点为 F1,F2.若以 A1A2 为直径的圆内切于菱形 F1B1F2B2,切点分别
为 A,B,C,D.则
(1)双曲线的离心率 e=________;
(2)菱形 F1B1F2B2 的面积 S1 与矩形 ABCD 的面积 S2 的比值S1
S2=________.
24.(2012·广东卷)在平面直角坐标系 xOy 中,已知椭圆 C: x2
a2+y2
b2=1(a>b>0)的离心
率 e= 2
3,且椭圆 C 上的点到点 Q(0,2)的距离的最大值为 3.
(1)求椭圆 C 的方程;
(2)在椭圆 C 上,是否存在点 M(m,n),使得直线 l:mx+ny=1 与圆 O:x2+y2=1 相交
于不同的两点 A、B,且△OAB 的面积最大?若存在,求出点 M 的坐标及对应的△OAB 的
面积;若不存在,请说明理由.
25.(2012·北京卷)已知曲线 C:(5-m)x2+(m-2)y2=8(m∈R).
(1)若曲线 C 是焦点在 x 轴上的椭圆,求 m 的取值范围;
(2)设 m=4,曲线 C 与 y 轴的交点为 A,B(点 A 位于点 B 的上方),直线 y=kx+4 与曲
线 C 交于不同的两点 M,N,直线 y=1 与直线 BM 交于点 G.求证:A,G,N 三点共线.
26.(2012·安徽卷)如图 1-5,点 F 1(-c,0),F2(c,0)分别是椭圆 C:x2
a2+y2
b2=1(a>b>0)
的左、右焦点,过点 F1 作 x 轴的垂线交椭圆 C 的上半部分于点 P,过点 F2 作直线 PF2 的垂
线交直线 x=a2
c 于点 Q.
(1)如果点 Q 的坐标是(4,4),求此时椭圆 C 的方程;
(2)证明:直线 PQ 与椭圆 C 只有一个交点.
27.(2012·北京卷)在直角坐标系 xOy 中,直线 l 过抛物线 y2=4x 的焦点 F,且与该抛
物线相交于 A,B 两点,其中点 A 在 x 轴上方,若直线 l 的倾斜角为 60°,则△OAF 的面积
为________.
28.(2012·福建卷)如图 1-4,椭圆 E:x2
a2+y2
b2=1(a>b>0)的左焦点为 F1,右焦点为 F2,
离心率 e=1
2,过 F1 的直线交椭圆于 A、B 两点,且△ABF2 的周长为 8.
(1)求椭圆 E 的方程;
(2)设动直线 l:y=kx+m 与椭圆 E 有且只有一个公共点 P,且与直线 x=4 相交于点 Q.
试探究:在坐标平面内是否存在定点 M,使得以 PQ 为直径的圆恒过点 M?若存在,求出点
M 的坐标;若不存在,说明理由.
图 1-4
29.(2012·课标全国卷)设抛物线 C:x2=2py(p>0)的焦点为 F,准线为 l,A 为 C 上一
点,已知以 F 为圆心,FA 为半径的圆 F 交 l 于 B,D 两点.
(1)若∠BFD=90°,△ABD 的面积为 4 2,求 p 的值及圆 F 的方程;
(2)若 A、B、F 三点在同一直线 m 上,直线 n 与 m 平行,且 n 与 C 只有一个公共点,
求坐标原点到 m,n 距离的比值.
30.(2012·课标全国卷)设点 P 在曲线 y= 1
2ex 上,点 Q 在曲线 y=ln(2x)上,则|PQ|的
最小值为( )
A.1-ln2 B. 2(1-ln2)
C.1+ln2 D. 2(1+ln2)
31.(2012·辽宁卷)如图 1-7,椭圆 C0:x2
a2+y2
b2=1(a>b>0,a,b 为常数),动圆 C1:
x2+y2=t21,b<t1<a.点 A1,A2 分别为 C0 的左,右顶点.C1 与 C0 相交于 A,B,C,D 四
点.
(1)求直线 AA1 与直线 A2B 交点 M 的轨迹方程;
(2)设动圆 C2:x2+y2=t 22与 C0 相交于 A′,B′,C′,D′四点,其中 b<t2<a,t1≠t2.若矩形
ABCD 与矩形 A′B′C′D′的面积相等.证明:t21+t 22为定值.
32.(2012·浙江卷)如图 1-6,椭圆 C:x2
a2+y2
b2=1(a>b>0)的离心率为1
2,其左焦点到点
P(2,1)的距离为 10.不过原点 O 的直线 l 与 C 相交于 A,B 两点,且线段 AB 被直线 OP 平
分.
(1)求椭圆 C 的方程;
(2)求△ABP 面积取最大值时直线 l 的方程.
33.(2012·江西卷)已知三点 O(0,0),A(-2,1),B(2,1),曲线 C 上任意一点 M(x,y)
满足|MA→
+MB→
|=OM→
·(OA→
+OB→
)+2.
(1)求曲线 C 的方程;
(2)动点 Q(x0,y0)(-2
6 1r = −
2 2x y =1 P 464 36
− 上一点 到双曲线右焦点的距离是 ,那么点
设 P 到左准线的距离是 d,由第二定义,得 ,解得 .
(2011 年高考全国卷理科 15)已知 F1、F2 分别为双曲线 C: - =1 的左、右焦点,
点 A∈C,点 M 的坐标为(2,0),AM 为∠F1AF2∠的平分线.则|AF2| = .
【答案】6
【解析】 ,由角平分线的性质得
又
(2011 年高考安徽卷理科 21)(本小题满分 13 分)
设 ,点 的坐标为(1,1),点 在抛物线 上运动,点 满足 ,
经过 点与 轴垂直的直线交抛物线于点 ,点 满足 ,求点 的轨迹方程
[
【解析】由 知 Q,M,P 三点在同一条垂直于 x 轴的直线上,故可设 ,
, ,则 ,即
①
再设 ,由 ,即 ,解得
②
将①代入②式,消去 得
③
又点 B 在抛物线 上,所以 ,再将③式代入得
20 10
8d
= 16d =
2
9
x 2
27
y
1 2( 6,0), (6,0)F F−
1 1
2 2
8 24
AF F M
AF MF
= = =
1 2 2 3 6AF AF− = × = 2 6AF∴ =
λ > 0 A B y x2= Q BQ QAλ=
Q x M P QM MPλ= P
QM MPλ= ( , )P x y
( , )Q x y0 ( , )M x x2 ( )x y y xλ2 2
0− = −
( ) ( )y x y x x yλ λ λ2 2 2
0 = − − = 1+ −
( , )B x y1 1 BQ QAλ= ( , ) ( , )x x y y x yλ1 0 1 0− − = 1− 1−
( )
( )
x x
y y
λ λ
λ λ
1
1 0
= 1+ −
= 1+ −
y0
( )
( ) ( )
x x
y x y
λ λ
λ λ λ λ
1
2 2
1
= 1+ −
= 1+ − 1+ −
y x2= y x2
1 1=
,即
,即
,因为 ,等式两边同时约去 得
这就是所求的点 的轨迹方程。
(2011 年高考浙江卷理科 21)(本题满分 15 分)已知抛物线 : ,圆 :
的圆心为点 M
(Ⅰ)求点 M 到抛物线 的准 线的距离;
(Ⅱ)已知点 P 是抛物线 上一点(异于原点),过点 P 作圆 的两条切线,交抛物线
于 A,B 两点,若过 M,P 两点的直线 垂直于 AB,求直线 的方程
【解析】(Ⅰ)由 得准 线方程为 ,由 得 M ,点 M
到抛物线 的准 线的距离为
(Ⅱ)设点 , , 由题意得 设
过点 的圆 的切线方程为 即 ① 则
即 设 , 的斜率为
( )则 是上述方
( ) ( ) [( ) ]x y xλ λ λ λ λ λ2 2 21+ − 1+ − = 1+ −
( ) ( ) ( ) ( )x y x xλ λ λ λ λ λ λ λ2 2 2 2 21+ − 1+ − = 1+ − 2 1+ +
( ) ( ) ( )x yλ λ λ λ λ λ2 1+ − 1+ − +1 = 0 λ > 0 ( )λ λ1+
x y2 − −1= 0
P
1C 2x y= 2C
2 2( 4) 1x y+ − =
1c
1c 2c
1c l l
2x y= 1
4y = − 2 2( 4) 1x y+ − = (0,4)
1c 1 174 ( )4 4
− − =
2
0 0( , )P x x 2
1 1( , )A x x 2
2 2( , )B x x 0 00, 1,x x≠ ≠ ± 1 2x x≠
P 2C 2
0 0( )y x k x x− = − 2
0 0y kx x kx= + −
2
0 0
2
| 4 | 1
1
kx x
k
+ − =
+
2 2 2 2 2
0 0 0 0( 1) 2 (4 ) ( 4) 1 0x k x x k x− − − + − − = PA PB 1 2,k k
1 2k k≠ 1 2,k k
程的两个不相等的根, 将代入①
得
直线 的方程为 .
(2011 年高考广东卷理科 19)设圆 C 与两圆 中 的
一个内切,另一个外切.
(1)求 C 的圆心轨迹 L 的方程.
(2)已知点 且 P 为 L 上动点,求 的最大值
及此时点 P 的坐标.
【解析】(1)解:设 C 的圆心的坐标为 ,由题设条件知
化简得 L 的方程为
2
0 0
1 2 2
0
2 (4 ) ,1
x xk k x
−+ = −
2 2
0
1 2 2
0
( 4) 1
1
xk k x
− −⋅ = −
2y x=
23 23( , )5 5
±
l 3 115 4115y x= ± +
2 2 2 25 4, 5 4x y x y+ = − + =( + ) ( )
3 5 4 5( ) 55 5M F, ,( ,0), MP FP−
( , )x y
2 2 2 2| ( 5) ( 5) | 4,x y x y+ + − − + =
2
2 1.4
x y− =
(2)解:过 M,F 的直线 方程为 ,将其代入 L 的方程得
解得
因 T1 在线段 MF 外,T2 在线段 MF 内,故
,若 P 不在直线 MF 上,在
中有
故 只在 T1 点取得最大值 2。
(2011 年高考陕西卷理科 17)(本小题满分 12 分)
如图,设 是圆珠笔 上的动点,点 D 是 在 轴上的投影,M 为 D 上
一点,且
(Ⅰ)当 的在圆上运动时,求点 M 的轨迹 C 的方程;
l 2( 5)y x= − −
215 32 5 84 0.x x− + =
1 2 1 2
6 5 14 5 6 5 2 5 14 5 2 5, , ( , ), ( , ).5 15 5 5 15 15x x l L T T= = −故 与 交点为
1 1| | | | | | 2,MT FT MF− = =
2 2| | | | | | 2.MT FT MF− < = MFP∆
| | | | | | 2.MP FP MF− < =
| | | |MP FP−
P 2 2 25x y+ = P x P
4
5MD PD=
P
(Ⅱ)求过点(3,0)且斜率为 的直线被 C 所截线段的长度。
即 。
线段 AB 的长度为
注:求 AB 长度时,利用韦达定理或弦长公式求得正确结果,同样给分。
(2011 年高考重庆卷理科 20)(本小题满分 12 分,第一问 4 分,第二问 8 分)
如图(20),椭圆的中心为原点 O,离心率 ,一条准线的方 程为 。
(Ⅰ)求该椭圆的标准 方程。
(Ⅱ)设动点 P 满足 ,其 中 M,N 是椭圆上的点。直线 OM 与 ON 的斜
率之积为 。问:是否存在两个定点 ,使得 为定值。若存在,求
的坐标;若不存在,说明理由。
解析:(Ⅰ)由 ,解得 ,
故椭圆的标准方程为
(Ⅱ)设 , ,则由 得
,即 ,
4
5
2 3 8 0x x+ − = 1 2
3 41 3 41,2 2x x
− +∴ = =
∴ 2 2 2
1 2 1 2 1 2
16( ) ( ) (1 )( )25AB x x y y x x= − + − = + −
41 414125 5
= × =
2
2e = 2 2x =
2OP OM ON= +
1
2
− 1 2F F、 1 2PF PF+ 1 2F F、
22 , 2 22
a ae c c
= = = 2 2 22, 2, 2a c b a c= = = − =
2 2
14 2
x y+ =
( ),P x y ( ) ( )1 1 2 2, , ,M x y N x y 2OP OM ON= +
( ) ( ) ( )1 1 2 2, , 2 ,x y x y x y= + 1 2 1 22 , 2x x x y y y= + = +
因为点 M,N 在椭圆 上,所以
故
,
设 分别为直线 OM,ON 的斜率,由题意知,
,因此 ,
所以 ,
所以 P 点是椭圆 上的点,设该椭圆的左右焦点为 ,则由
椭圆的定义, 为定值,又因 ,因此两焦点的坐
标分别为
(2011 年高考四川卷理科 21) (本小题共 l2 分)
椭圆有两顶点 A(-1,0)、B(1 ,0),过其焦点 F(0,1)的直线 l 与椭圆交于 C、D 两
点,并与 x 轴交于点 P.直线 AC 与直线 BD 交于点 Q.
(I)当| CD | = 时,求直线 l 的方程;
(II)当点 P 异于 A、B 两点时,求证: 为定值.
2 2
14 2
x y+ = 2 2 2 2
1 1 2 22 4, 2 4x y x y+ = + =
( ) ( )2 2 2 2 2 2
1 2 1 2 1 2 1 22 4 4 2 4 4x y x x x x y y y y+ = + + + + +
( ) ( ) ( )2 2 2 2
1 1 2 2 1 2 1 22 4 2 4 2x y x y x x y y= + + + + +
( )1 2 1 220 4 2x x y y= + +
,OM ONk k
1 2
1 2
1= =- 2OM ON
y yk k x x 1 2 1 22 =0x x y y+
2 22 20x y+ =
( ) ( )
2 2
2 2 1
2 5 10
x y+ = 1 2F F、
1 2PF PF+ ( ) ( )2 2
2 5 10 10c = + =
( ) ( )1 210,0 10,0F F− 、
3 22
OP OQ•
(2011 年高考全国卷理科 21)已知 O 为坐标原点,F 为椭圆 在 y 轴正半轴上
的焦点,过 F 且斜率为 的直线 与 C 交与 A、B 两点,点 P 满 足
(Ⅰ)证明:点 P 在 C 上;(Ⅱ)设点 P 关于点 O 的对称点为 Q,
证明:A、P、B、Q 四点在同一圆上.
【解析】: (Ⅰ)证明:由 , ,
由
设
, ,
,
, 故点 P 在 C 上
2
2: 12
yC x + =
- 2 l 0.OA OB OP+ + =
2
2 1 (0,1)2
yx F+ = 得 : 2 1l y x= − +
22
2
1 2
4 2 2 1 0
12
y x
x xyx
= − − − =
+ =
得
1 1 1 1 1
2 2 8 4 4 ( 1)( , ), ( , ), 2 4A x y B x y x
− − × × −= ×则
2 6
4
−= 2
2 2 8 4 4 ( 1) 2 6
2 4 4x
+ − × × − += =×
1
2 6 3 12 14 2y
− += − × + =
2
2 6 1 32 14 2y
+ −= − × + = 0.OA OB OP+ + =
1 2
1 2
2( ) 2
( ) 1
p
p
x x x
y y y
= − + = −∴
= − + = −
2 2
2 22 1( ) 12 2 2
p
p
yx + = − + =
(Ⅱ)法一:点 P , P 关于点 O 的对称点为 Q, ,
,即 ,
同理 即 , A、P、B、Q 四点在同一
圆上.
法二:由已知有 则 的中垂线为: 设 、 的中点为
∴
∴ 则 的中垂线为:
则 的中垂线与 的中垂线的交点为 ∴
到直线 的距离为
∴ 即
∴ 、 、 、 四点在同一圆上。
(2011 年高考北京卷理科 19)(本小题共 14 分)
已知椭圆 .过点(m,0)作圆 的切线 I
2( , 1)2
− −
2( ,1)2Q∴
2
2
1 1 1
2 2
11 1
3 1( ) 11 1 1 2 112 2 2 6 1( )22 2 4 2
AQ AP
y y yK K
xx x
+ −− − − −= ⋅ = = = −
−−− − − −
90PAQ∠ =
1PB BQK K = − 90PBQ∠ = ∴ 180PAQ PBQ∠ + ∠ =
1,2
2Q PQ xy 2
2−= A B
( )33, yxD
( ) ( )
=+−++−=+=
=+=
2
1
2
1212
2
4
2
2
1121
3
21
3
xxyyy
xxx
2
1,4
2D AB
4
1
2
2 += xy
PQ AB
−
8
1,8
2'O
8
113|||| '' == QOPO
−
8
1,8
2'O AB
8
33
3
|18
1
8
22|
=
−+
−×
=d
( ) ( ) ( )[ ]
2
2343|| 21
2
21
2
21
2
21 =−+=−+−= xxxxyyxxAB
8
113
2
|||||| 2
2
'' =+
== dABBOAO |||||||| '''' QOPOBOAO ===
A P B Q
2
2: 14
xG y+ = 2 2 1x y+ =
交椭圆 G 于 A,B 两点.
(I)求椭圆 G 的焦点坐标和离心率;
(II)将 表示为 m 的函数,并求 的最大值.
此时
当 m=-1 时,同理可得
当 时,设切线 l 的方程为
由
设 A、B 两点的坐标分别为 ,则
又由 l 与圆
所以
AB AB
3|| =AB
3|| =AB
1|| >m ),( mxky −=
0448)41(
.14
),(
22222
2
2 =−+−+
=+
−=
mkmxkxk
yx
mxky
得
),)(,( 2211 yxyx
2
22
212
2
21 41
44,41
8
k
mkxxk
mkxx +
−=+=+
.1,1
1
||,1 222
2
22 +==
+
=+ kkm
k
kmyx 即得相切
2
12
2
12 )()(|| yyxxAB −+−=
]41
)44(4
)41(
64)[1( 2
22
22
4
2
k
mk
k
mkk +
−−++=
2
由于当 时,
所以 .
因为
且当 时,|AB|=2,所以|AB|的最大值为 2.
【2010 年高考真题】
(2010 浙江理数)(8)设 、 分别为双曲线 的左、右焦点.
若在双曲线右支上存在点 ,满足 ,且 到直线 的距离等于双曲线的实
轴长,则该双曲线的渐近线方程为
(A) (B) (C) (D)
解析:利用题设条件和双曲线性质在三角形中寻找等量关系,得出 a 与 b 之间的等量关
系。
答案:C
(2010 全国卷 2 理数)(12)已知椭圆 的离心率为 ,过
右焦点 且斜率为 的直线与 相交于 两点.若 ,则
(A)1 (B) (C) (D)2
【答案】B
【解析】设直线 l 为椭圆的有准线,e 为离心率,过 A,B 分别作 AA1,BB1 垂直于 l,
A1,B 为垂足,过 B 作 BE 垂直于 AA1 与 E,由第二定义得, ,
由 , 得 , ∴
.3
||34
2 +=
m
m
3±=m ,3|| =AB
),1[]1,(,3
||34|| 2
+∞−−∞∈+= mm
mAB
,2
||
3||
34
3
||34|| 2
≤
+
=+=
mmm
mAB
3±=m
1F 2F
2 2
2 2 1( 0, 0)x y a ba b
− = > >
P 2 1 2PF F F= 2F 1PF
3 4 0x y± = 3 5 0x y± = 4 3 0x y± = 5 4 0x y± =
2 2
2 2: 1( 0)x yC a ba b
+ = > > 3
2
F ( 0)k k> C A B、 3AF FB= k =
2 3
即 k= ,故选 B.
(2010 辽宁理数) (9)设双曲线的—个焦点为 F;虚轴的—个端点为 B,如果直线 FB
与该双曲线的一条渐 近线垂直,那么此双曲线的离心率为
(A) (B) (C) (D)
【答案】D
(2010 辽宁理数)(7)设抛物线 y2=8x 的焦点为 F,准线为 l,P 为抛物线上一点,PA⊥l,A
为垂足.如果直线 AF 的斜率为 ,那么|PF|=
(A) (B)8 (C) (D) 16
【答案】B
【解析】抛物线的焦点 F(2,0),直线 AF 的方程为 ,所以点
、 ,从而|PF|=6+2=8
(2010 重庆理数)(10)到两互相垂直的异面直线的距离相等的点,在过其中一条直线
且平行于另一条直线的平面内的轨迹是
A. 直线 B. 椭圆 C. 抛物线 D. 双曲线
解析:排除法 轨迹是轴对称图形,排除 A、C,轨迹与已知直线不能有交点,排除 B
答案:D
(2010 四川理数)(9)椭圆 的右焦点 ,其右准线与 轴的交
2 3 3 1
2
+ 5 1
2
+
- 3
4 3 8 3
3( 2)y x= − −
( 2,4 3)A − (6,4 3)P
2 2
2 2 1( )x y a ba b
+ = > > 0 F x
点为 A,在椭圆上存在点 P 满足线段 AP 的垂直平分线过点 ,则椭圆离心率的取值范围是
(A) (B) (C) (D)
解析:由题意,椭圆上存在点 P,使得线段 AP 的垂直平分线过点 ,
即 F 点到 P 点与 A 点的距离相等
答案:D
(2010 天津理数)(5)已知双曲线 的一条渐近线方程是 y=
,它的一个焦点在抛物线 的准线上,则双曲线的方程为
(A) (B)
(C) (D)
【答案】B
【解析】本题主要考查双曲线与抛物线的几何性质与标准方程,属于容易题。
F
20, 2
10,2
)2 1,1 − 1,12
F
2 2
2 2 1( 0, 0)x y a ba b
− = > >
3x 2 24y x=
2 2
136 108
x y− =
2 2
19 27
x y− =
2 2
1108 36
x y− =
2 2
127 9
x y− =
依题意知 ,所以双曲线的方程为
(2010 山东理数)(7)由曲线 y= ,y= 围成的封闭图形面积为
(A) (B) (C) (D)
【答案】A
【解析】由题意得:所求封闭图形的面积为 ,故选 A。
(2010 安徽理数)5、双曲线方程为 ,则它的右焦点坐标为
A、 B、 C、 D、
【答案】C
【解析】双曲线的 , , ,所以右焦点为 .
(2010 湖北理数)9.若直线 y=x+b 与曲线 有公共点,则 b 的取值范围
是
【答案】C
【解析】曲线方程可化简为 ,即表示圆心为(2,3)半
径为 2 的半圆,依
据数形结合,当直线 与此半圆相切时须满足圆心(2,3)到直线 y=x+b 距
离等于 2,解得
,因为是下半圆故可得 (舍),当直线过(0,3)
2 2
2 2 2
3
6 9, 27
b
a
c a b
c a b+
=
= ⇒ = =
=
2 2
19 27
x y− =
2x 3x
1
12
1
4
1
3
7
12
1 2 3
0 x -x )dx=∫( 1 1 11- 1=3 4 12
× ×
2 22 1x y− =
2 ,02
5 ,02
6 ,02
( )3,0
2 2 11, 2a b= = 2 3
2c = 6
2c = 6 ,02
23 4y x x= − −
2 2( 2) ( 3) 4(1 3)x y y− + − = ≤ ≤
y x b= +
1 2 2 1 2 2b b= + = −或 1 2 2b = +
时,解得 b=3,故
所以 C 正确.
(2010 福建理数)7.若点 O 和点 分别是双曲线 的中心和左
焦点,点 P 为双曲线右支上的任意一点,则 的取值范围为 ( )
A. B. C. D.
【答案】B
【解析】因为 是已知双曲线的左焦点,所以 ,即 ,所以双曲
(2010 福建理数)2.以抛物线 的焦点为圆心,且过坐标原点的圆的方程为( )
A. B. C. D.
【答案】D
【解析】因为已知抛物线的焦点坐标为(1,0),即所求圆的圆心,又圆过原点,所以
圆的半径为 ,故所求圆的方程为 ,即 ,选 D。
(2010 浙江理数)(13)设抛物线 的焦点为 ,点
.若线段 的中点 在抛物线上,则 到该抛物线准线的距离为
_____________。
解析:利用抛物线的定义结合题设条件可得出 p 的值为 ,B 点坐标为( )
1 2 2 3,b− ≤ ≤
( 2,0)F −
2
2
2 1(a>0)a
x y− =
OP FP⋅
[3-2 3, )+∞ [3 2 3, )+ +∞ 7[- , )4
+∞ 7[ , )4
+∞
( 2,0)F − 2 1 4a + = 2 3a =
2 4y x=
2 2x +y +2x=0 2 2x +y +x=0 2 2x +y -x=0 2 2x +y -2x=0
r=1 2 2x-1) +y =1( 2 2x -2x+y =0
2 2 ( 0)y px p= > F
(0,2)A FA B B
2 14
2 ,
所以点 B 到抛物线准线的距离为 ,本题主要考察抛物线的定义及几何性质,属容
易题
(2010 全国卷 2 理数)(15)已知抛物线 的准线为 ,过 且
∴ 2.
(2010 江西理数)15.点 在双曲线 的右支上,若点 A 到右焦点的
距离等于 ,则 =
【答案】 2
【解析】考查圆锥曲线的基本概念和第二定义的转化,读取 a=2.c=6, ,
( 2010 重 庆 理 数 ) (14) 已 知 以 F 为 焦 点 的 抛 物 线 上 的 两 点 A 、 B 满 足
, 则 弦 AB 的 中 点 到 准 线 的 距 离 为
___________.
解析:设 BF=m,由抛物线的定义知
中,AC=2m,AB=4m,
直线 AB 方程为
3 24
2: 2 ( 0)C y px p= > l (1,0)M
p =
0 0( )A x y,
2 2
14 32
x y− =
02x 0x
r ed
= 3r d⇒ =
2
0 0 02 3( ) 2ax x xc
= − ⇒ =
2 4y x=
3AF FB=
mBBmAA == 11 ,3
ABC∆∴ 3=ABk
)1(3 −= xy
与抛物线方程联立消 y 得
所以 AB 中点到准线距离为
(2010 江苏卷)6、在平面直角坐标系 xOy 中,双曲线 上一点 M,点 M
的横坐标是 3,则 M 到双曲线右焦点的距离是___▲_______
答案:4
解析:考查双曲线的定义。 , 为点 M 到右准线 的距离, =2,
MF=4。
(2010 浙江理数)(21) (本题满分 15 分)已知 m>1,直线 ,椭圆
, 分别为椭圆 的左、右焦点.
(Ⅰ)当直线 过右焦点 时,求直线 的方程;
(Ⅱ)设直线 与椭圆 交于 两点, , 的重心分别为 .若原
点 在以线段 为直径的圆内,求实数 的取值范围.
解析:本题主要考察椭圆的几何性质,直线与椭圆,点与圆的位置关系等基础知识,同
时考察解析几何的基本思想方法和综合解题能力。
( Ⅰ ) 解 : 因 为 直 线 经 过 , 所 以
03103 2 =+− xx
3
813
512
21 =+=++ xx
1124
22
=− yx
4 22
MF ed
= = = d 1x = d
2
: 02
ml x my− − =
2
2
2: 1xC ym
+ = 1, 2F F C
l 2F l
l C ,A B 1 2AF F 1 2BF F ,G H
O GH m
:l
2
02
mx my− − = 2
2 ( 1,0)F m −
,得 ,
则由 ,知 ,
且有 。
由于 ,
故 为 的中点,
由 ,
可知
设 是 的中点,则 ,
由题意可知
即
即
2
2 1 2
mm − = 2 2m =
2
2 28( 1) 8 04
mm m∆ = − − = − + > 2 8m <
2
1 2 1 2
1,2 8 2
m my y y y+ = − = −
1 2( ,0), ( ,0),F c F c−
O 1 2F F
2 , 2AG GO BH HO= =
1 1 2 1( , ), ( , ),3 3 3 3
x y x yG h
2 2
2 1 2 1 2( ) ( )
9 9
x x y yGH
− −= +
M GH 1 2 1 2( , )6 6
x x y yM
+ +
2 ,MO GH<
2 2
2 21 2 1 2 1 2 1 2( ) ( )4[( ) ( ) ]6 6 9 9
x x y y x x y y+ + − −+ < +
1 2 1 2 0x x y y+ <
而
设椭圆 C: 的左焦点为 F,过点 F 的直线与椭圆 C 相交于 A,B
两点,直线 l 的倾斜角为 60o, .
(1)求椭圆 C 的离心率;
(2)如果|AB|= ,求椭圆 C 的方程.
【解析】解:
设 ,由题意知 <0, >0.
(Ⅰ)直线 l 的方程为 ,其中 .
联立 得
解得
因为 ,所以 .
2 2
1 2 1 2 1 2 1 2( )( )2 2
m mx x y y my my y y+ = + + +
2
2 1( 1 ( )8 2
mm= + −)
2 2
2 2 1( 0)x y a ba b
+ = > >
2AF FB=
15
4
1 1 2 2( , ), ( , )A x y B x y 1y 2y
3( )y x c= − 2 2c a b= −
2 2
2 2
3( ),
1
y x c
x y
a b
= − + =
2 2 2 2 4(3 ) 2 3 3 0a b y b cy b+ + − =
2 2
1 22 2 2 2
3 ( 2 ) 3 ( 2 ),3 3
b c a b c ay ya b a b
− + − −= =+ +
2AF FB=
1 22y y− =
(2010 江西理数)21. (本小题满分 12 分)
设椭圆 ,抛物线 。
(1)若 经过 的两个焦点,求 的离心率;
(2)设 A(0,b), ,又 M、N 为 与 不在 y 轴上的两个交点,
若△AMN 的垂心为 ,且△QMN 的重心在 上,求椭圆 和抛物线
的方程。
【解析】考查椭圆和抛物线的定义、基本量,通过交点三角形来确认方程。
(1)由已知椭圆焦点(c,0)在抛物线上,可得: ,由
。
(2) 由 题 设 可 知 M 、 N 关 于 y 轴 对 称 , 设
,由 的垂心为 B,有
。
由点 在抛物线上, ,解得:
故 ,得 重心坐标 .
2 2
1 2 2: 1( 0)x yC a ba b
+ = > > 2 2
2 :C x by b+ =
2C 1C 1C
53 3 4Q
, 1C 2C
3
4B b
0, 2C 1C 2C
2 2c b=
2
2 2 2 2
2
1 22 , 2 2
ca b c c ea
= + = = ⇒ =有
1 1 1 1 1( , ), ( , )( 0)M x y N x y x− > AMN∆
2
1 1 1
30 ( )( ) 04BM AN x y b y b⋅ = ⇒ − + − − =
1 1( , )N x y 2 2
1 1x by b+ = 1 1 ( )4
by y b= − =或 舍去
1
5 5 5, ( , ), ( , )2 2 4 2 4
b bx b M b N b= − − − QMN∆ ( 3, )4
b
由重心在抛物线上得: , ,又
因为 M、N 在椭圆上得: ,椭圆方程为 ,抛物线方程为 。
(2010 北京理数)(19)(本小题共 14 分)www.@ks@5u.com
在平面直角坐标系 xOy 中,点 B 与点 A(-1,1)关于原点 O 对称,P 是动点,且直线 AP
与 BP 的斜率之积等于 .
(Ⅰ)求动点 P 的轨迹方程;
(Ⅱ)设直线 AP 和 BP 分别与直线 x=3 交于点 M,N,问:是否存在点 P 使得△PAB 与
△PMN 的面积相等?若存在,求出点 P 的坐标;若不存在,说明理由。
【解析】(I)解:因为点 B 与 A 关于原点 对称,所以点 得坐标为
.
设点 的坐标为
由题意得
化简得 .
故动点 的轨迹方程为
( II ) 解 法 一 : 设 点 的 坐 标 为 , 点 , 得 坐 标 分 别 为
, .
则直线 的方程为 ,直线 的方程为
令 得 , .
于是 得面积
2
23 , =24
b b b+ = 所以 1 1( 5, ), ( 5, )2 2M N− − −
2 16
3a =
2 2
16
3
14
x y+ = 2 2 4x y+ =
1
3
−
( 1,1)− O B
(1, 1)−
P ( , )x y
1 1 1
1 1 3
y y
x x
− + = −+ −
2 23 4( 1)x y x+ = ≠ ±
P 2 23 4( 1)x y x+ = ≠ ±
P 0 0( , )x y M N
(3, )My (3, )Ny
AP 0
0
11 ( 1)1
yy xx
−− = ++ BP 0
0
11 ( 1)1
yy xx
++ = −−
3x = 0 0
0
4 3
1M
y xy x
+ −= +
0 0
0
2 3
1N
y xy x
− += −
PMN
2
0 0 0
0 2
0
| | (3 )1 | | (3 )2 | 1|PMN M N
x y xS y y x x
+ −= − − = −
故存在点 使得 与 的面积相等,此时点 的坐标为 .
解法二:若存在点 使得 与 的面积相等,设点 的坐标为
则 .
因为 ,
所以
所以
即 ,解得
因为 ,所以
故 存 在 点 S 使 得 与 的 面 积 相 等 , 此 时 点 的 坐 标 为
.
P PAB PMN P 5 33( , )3 9
±
P PAB PMN P 0 0( , )x y
1 1| | | | sin | | | | sin2 2PA PB APB PM PN MPN∠ = ∠
sin sinAPB MPN∠ = ∠
| | | |
| | | |
PA PN
PM PB
=
0 0
0
| 1| | 3 |
| 3 | | 1|
x x
x x
+ −=− −
2 2
0 0(3 ) | 1|x x− = − 0x 5
3
=
2 2
0 03 4x y+ = 0
33
9y = ±
P PAB PMN P
5 33( , )3 9
±
(2010 四川理数)(20)(本小题满分 12 分)
已知定点 A(-1,0),F(2,0),定直线 l:x= ,不在 x 轴上的动点 P 与点 F 的距离是
它到直线 l 的距离的 2 倍.设点 P 的轨迹为 E,过点 F 的直线交 E 于 B、C 两点,直线 AB、AC
分别交 l 于点 M、N
(Ⅰ)求 E 的方程;
(Ⅱ)试判断以线段 MN 为直径的圆是否过点 F,并说明理由. w_w w. k#s5_u.c o*
【解析】解:(1)设 P(x,y),则
化简得 x2- =1(y≠0)………………………………………………………………4 分
(2)①当直线 BC 与 x 轴不垂直时,设 BC 的方程为 y=k(x-2)(k≠0)
与双曲线 x2- =1 联立消去 y 得
(3-k)2x2+4k2x-(4k2+3)=0
由题意知 3-k2≠0 且△>0
设 B(x1,y1),C(x2,y2),
则
y1y2=k2(x1-2)(x2-2)=k2[x1x2-2(x1+x2)+4]
=k2( +4)
= w_w w. k#s5_u.c o*m
因为 x1、x2≠-1
所以直线 AB 的方程为 y= (x+1)
1
2
2 2 1( 2) 2 | |2x y x− + = −
2
3
y
2
3
y
2
1 2 2
2
1 2 2
4
3
4 3
3
kx x k
kx x k
+ = − + = −
2 2
2 2
4 3 8
3 3
k k
k k
+ −− −
2
2
9
3
k
k
−
−
1
1 1
y
x +
=0
②当直线 BC 与 x 轴垂直时,起方程为 x=2,则 B(2,3),C(2,-3)
AB 的方程为 y=x+1,因此 M 点的坐标为( ),
同理可得
因此 =0w_w w. k#s5_u.c o*m
综上 =0,即 FM⊥FN
故以线段 MN 为直径的圆经过点 F………………………………………………12 分
(2010 天津理数)(20)(本小题满分 12 分)
已知椭圆 的离心率 ,连接椭圆的四个顶点得到的菱形的
面积为 4。
(1) 求椭圆的方程;
(2) 设 直 线 与 椭 圆 相 交 于 不 同 的 两 点 , 已 知 点 的 坐 标 为
( ),点 在线段 的垂直平分线上,且 ,求 的值
【解析】本小题主要考察椭圆的标准方程和几何性质,直线的方程,平面向量等基础知
识,考查用代数方法研究圆锥曲线的性质及数形结合的思想,考查运算和推理能力,满分 12
分
1 3,2 2
3 3( , )2 2FM = −
3 3( , )2 2FN = − −
23 3 3( ) ( )2 2 2FM FN = − + × −
FM FN
2 2
2 2 1( 0x y a ba b
+ = > > ) 3
2e =
l ,A B A
,0a− 0(0, )Q y AB 4QA QB =
0y
(2)解:由(1)可知 A(-2,0)。设 B 点的坐标为(x1,,y1),直线 l 的斜率为 k,则直线 l
的方程为 y=k(x+2),
于是 A,B 两点的坐标满足方程组
由方程组消去 Y 并整理,得
由 得
设线段 AB 是中点为 M,则 M 的坐标为
以下分两种情况:
(1)当 k=0 时,点 B 的坐标为(2,0)。线段 AB 的垂直平分线为 y 轴,于是
(2)当 K 时,线段 AB 的垂直平分线方程为
令 x=0,解得
2
2
( 2)
14
y k x
x y
= + + =
2 2 2 2(1 4 ) 16 (16 4) 0k x k x k+ + + − =
2
1 2
16 42 ,1 4
kx k
−− = +
2
1 12 2
2 8 4, ,1 4 1 4
k kx yk k
−= =+ +从而
2
2 2
8 2( , )1 4 1 4
k k
k k
− + +
0 0 0( 2, y ), (2, = 2QA QB y QA QB y
→ → → →
= − − = − ±)由 4,得 = 2
0≠
2
2 2
2 1 8( )1 4 1 4
k kY xk k k
− = ++ +
0 2
6
1 4
ky k
= +
在平面直角坐标系 中,如图,已知椭圆 的左、右顶点为 A、B,右焦
点为 F。设过点 T( )的直线 TA、TB 与椭圆分别交于点 M 、 ,其
中 m>0, 。
(1)设动点 P 满足 ,求点 P 的轨迹;
(2)设 ,求点 T 的坐标;
(3)设 ,求证:直线 MN 必过 x 轴上的一定点
(其坐标与 m 无关)。
【解析】本小题主要考查求简单曲线的方程,考查方直线与椭圆的方程等基础知识。考
查运算求解能力和探究问题的能力。满分 16 分。
(1)设点 P(x,y),则:F(2,0)、B(3,0)、A(-3,0)。
由 ,得 化简得 。
故所求点 P 的轨迹为直线 。
(2)将 分别代入椭圆方程,以及 得:M(2, )、N
( , )
xoy 159
22
=+ yx
mt, ),( 11 yx ),( 22 yxN
0,0 21 <> yy
422 =− PBPF
3
1,2 21 == xx
9=t
422 =− PBPF 2 2 2 2( 2) [( 3) ] 4,x y x y− + − − + = 9
2x =
9
2x =
3
1,2 21 == xx 0,0 21 <> yy 5
3
1
3
20
9
−
联立方程组,解得: ,
所以点 T 的坐标为 。
(3)点 T 的坐标为
直线 MTA 方程为: ,即 ,
直线 NTB 方程为: ,即 。
分别与椭圆 联立方程组,同时考虑到 ,
解得: 、 。
( 方 法 一 ) 当 时 , 直 线 MN 方 程 为 :
7
10
3
x
y
= =
10(7, )3
(9, )m
0 3
0 9 3
y x
m
− +=− + ( 3)12
my x= +
0 3
0 9 3
y x
m
− −=− − ( 3)6
my x= −
159
22
=+ yx
1 23, 3x x≠ − ≠
2
2 2
3(80 ) 40( , )80 80
m mM m m
−
+ +
2
2 2
3( 20) 20( , )20 20
m mN m m
− −+ +
1 2x x≠
2
2 2
2 2
2 2 2 2
20 3( 20)
20 20
40 20 3(80 ) 3( 20)
80 20 80 20
m my xm m
m m m m
m m m m
−+ −+ += − −+ −+ + + +
若 ,则 ,直线 MD 的斜率 ,
直线 ND 的斜率 ,得 ,所以直线 MN 过 D 点。
因此,直线 MN 必过 轴上的点(1,0)。
【2009 年高考真题】
1.(2009·山东理)设双曲线 的一条渐近线与抛物线 y=x +1 只有一个公共
点,则双曲线的离心率为( ).
A. B. 5 C. D.
解析:双曲线 的一条渐近线为 ,由方程组 ,消去 y,得
有唯一解,所以△= ,
所以 , ,故选 D.
答案:D.
(2009·安徽理)下列曲线中离心率为 的是
【解析】由 得 ,选 B
【答案】B
(2009·宁夏海南理)双曲线 - =1 的焦点到渐近线的距离为
(A) (B)2 (C) (D)1
1 2x x≠ 2 10m ≠ 2
2 2
2
40
1080
240 3 40180
MD
m
mmk m m
m
+= =− −−+
2
2 2
2
20
1020
3 60 40120
ND
m
mmk m m
m
−
+= =− −−+
MD NDk k=
x
12
2
2
2
=−
b
y
a
x 2
4
5
2
5 5
12
2
2
2
=−
b
y
a
x xa
by =
2 1
by xa
y x
=
= +
2 1 0bx xa
− + = 2( ) 4 0b
a
− =
2b
a
=
2 2
21 ( ) 5c a b be a a a
+= = = + =
6
2
6
2e =
2 2 2
2 2 2
3 3 1,1 ,2 2 2
c b b
a a a
= + = =
2
4
x 2
12
y
2 3 3
解 析 : 双 曲 线 - =1 的 焦 点 (4,0) 到 渐 近 线 的 距 离 为
,选 A
答案:A
(2009·天津理)设抛物线 =2x 的焦点为 F,过点 M( ,0)的直线与抛物线相交
于 A,B 两点,与抛物线的准线相交于 C, =2,则 BCF 与 ACF 的面积之比
=
(A) (B) (C) (D)
解析:由题知 ,
又
由 A、B、M 三点共线有 即 ,故 ,
∴ ,故选择 A。
2
4
x 2
12
y 3y x=
3 4 0
2 32d
× −
= =
2y 3
BF ∆ ∆ BCF
ACF
S
S
∆
∆
4
5
2
3
4
7
1
2
12
12
2
1
2
1
+
+=
+
+
==
∆
∆
A
B
A
B
ACF
BCF
x
x
x
x
AC
BC
S
S
32
322
1|| −=⇒=⇒=+= BBB yxxBF
BM
BM
AM
AM
xx
yy
xx
yy
−
−=−
−
2
33
30
3
20
−
+=
−
−
A
A
x
x 2=Ax
5
4
14
13
12
12 =+
+=+
+=
∆
∆
A
B
ACF
BCF
x
x
S
S
答案:A
(2009··浙江理)过双曲线 的右顶点 作斜率为 的直线,
该直线与双曲线的两条渐近线的交点分别为 .若 ,则双曲线的离心率是 ( )
A. B. C. D.
答案:C
解析:对于 ,则直线方程为 ,直线与两渐近线的交点为 B,C,
(2009·宁夏海南理)设已知抛物线 C 的顶点在坐标原点,焦点为 F(1,0),直线 l 与抛
物线 C 相交于 A,B 两点。若 AB 的中点为(2,2),则直线 的方程为_____________.
解 析 : 抛 物 线 的 方 程 为 ,
答案:y=x
(2009·天津理)若圆 与圆 (a>0)的公共弦的长为
,
则 ___________ 。
答案:1
解 析 : 由 知 的 半 径 为 , 由 图 可 知
解之得
2 2
2 2 1( 0, 0)x y a ba b
− = > > A 1−
,B C 1
2AB BC=
2 3 5 10
( ),0A a 0x y a+ − =
ι
2 4y x=
( ) ( )
( )
2
1 1
1 1 2 2 1 2 2
2 2
2 2 1 2
1 2 1 2
1 2 1 2
4, , , ,
4
44 1
y xA x y B x y x x
y x
y yy y x x x x y y
=≠ =
−− = − ∴ = =− +
∴
则有 ,
两式相减得, ,
直线l 的方程为y- 2=x- 2, 即y=x
2 2 4x y+ = 2 2 2 6 0x y ay+ + − =
2 3
=a
2 2 2 6 0x y ay+ + − = 26 a+
222 )3()1(6 =−−−+ aa 1=a
(2009·山东理)(本小题满分 14 分)
设椭圆 E: (a,b>0)过 M(2, ) ,N( ,1)两点,O 为坐标原点,
(I)求椭圆 E 的方程;
(II)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆 E 恒有两个交点
A,B,且 ?若存在,写出该圆的方程,并求|AB |的取值范围,若不存在说明理由。
【解析】解:(1)因为椭圆 E: (a,b>0)过 M(2, ) ,N( ,1)两点,
所以 解得 所以 椭圆 E 的方程为
(2)假设存在圆心在原点的圆,使得该圆的任意一条切线与椭圆 E 恒有两个交点
A,B, 且 , 设 该 圆 的 切 线 方 程 为 解 方 程 组 得
,即 ,
则△= ,即
,
要 使 , 需 使 , 即 , 所 以
, 所 以 又 , 所 以 , 所 以
,即 或 ,因为直线 为圆心在原点的圆的一条切
2 2
2 2 1x y
a b
+ = 2 6
OA OB⊥
2 2
2 2 1x y
a b
+ = 2 6
2 2
2 2
4 2 1
6 1 1
a b
a b
+ =
+ =
2
2
1 1
8
1 1
4
a
b
=
=
2
2
8
4
a
b
=
=
2 2
18 4
x y+ =
OA OB⊥ y kx m= + 2 2
18 4
x y
y kx m
+ =
= +
2 22( ) 8x kx m+ + = 2 2 2(1 2 ) 4 2 8 0k x kmx m+ + + − =
2 2 2 2 2 216 4(1 2 )(2 8) 8(8 4) 0k m k m k m− + − = − + > 2 28 4 0k m− + >
2 2 2 2 2 2
2 2 2
1 2 1 2 1 2 1 2 2 2 2
(2 8) 4 8( )( ) ( ) 1 2 1 2 1 2
k m k m m ky y kx m kx m k x x km x x m mk k k
− −= + + = + + + = − + =+ + +
OA OB⊥
1 2 1 2 0x x y y+ =
2 2 2
2 2
2 8 8 01 2 1 2
m m k
k k
− −+ =+ +
2 23 8 8 0m k− − =
2
2 3 8 08
mk
−= ≥ 2 28 4 0k m− + >
2
2
2
3 8
m
m
>
≥
2 8
3m ≥ 2 6
3m ≥ 2 6
3m ≤ − y kx m= +
任意一条切线与椭圆 E 恒有两个交点 A,B,且 .
因为 ,
所 以
,
,
①当 时
因为 所以 ,
所以 ,
所以 当且仅当 时取”=”.
OA OB⊥
1 2 2
2
1 2 2
4
1 2
2 8
1 2
kmx x k
mx x k
+ = − + − = +
2 2 2
2 2 2
1 2 1 2 1 2 2 2 2 2
4 2 8 8(8 4)( ) ( ) 4 ( ) 41 2 1 2 (1 2 )
km m k mx x x x x x k k k
− − +− = + − = − − × =+ + +
( ) 2 2
22 2 2 2
1 2 1 2 1 2 2 2
8(8 4)| | ( ) (1 )( ) (1 ) (1 2 )
k mAB x x y y k x x k k
− += − + − = + − = + +
4 2 2
4 2 4 2
32 4 5 1 32[1 ]3 4 4 1 3 4 4 1
k k k
k k k k
+ += ⋅ = ++ + + +
0k ≠
2
2
32 1| | [1 ]13 4 4
AB
k k
= +
+ +
2
2
14 4 8k k
+ + ≥
2
2
1 10 1 84 4k k
< ≤
+ +
2
2
32 32 1[1 ] 1213 3 4 4k k
< + ≤
+ +
4 6 | | 2 33 AB< ≤ 2
2k = ±
② 当 时, .
③ 当 AB 的斜率不存在时, 两个交点为 或 ,所以
此时 ,
综上, |AB |的取值范围为 即:
( 2009·广 东 理 )(本小题满分 14 分)
已 知 曲 线 与 直 线 交 于 两 点 和 , 且
.记曲线 在点 和点 之间那一段 与线段 所围成的平面区域(含边界)为
.设点 是 上的任一点,且点 与点 和点 均不重合.
(1)若点 是线段 的中点,试求线段 的中点 的轨迹方程;
(2)若曲线 与 有公共点,试求 的最小值.
【解析】解:(1)联立 与 得 ,则 中点 ,
设线段 的中点 坐标为 ,则 ,即 ,
又点 在曲线 上,
∴ 化简可得 ,又点 是 上的任一点,且不与点
和 点 重 合 , 则 , 即 , ∴ 中 点 的 轨 迹 方 程 为
( ).
0k = 4 6| | 3AB =
2 6 2 6( , )3 3
± 2 6 2 6( , )3 3
− ±
4 6| | 3AB =
4 6 | | 2 33 AB≤ ≤ 4| | [ 6,2 3]3AB ∈
2:C y x= : 2 0l x y− + = ( , )A AA x y ( , )B BB x y
A Bx x< C A B L AB
D ( , )P s t L P A B
Q AB PQ M
2 2 2 51: 2 4 025G x ax y y a− + − + + = D a
2xy = 2+= xy 2,1 =−= BA xx AB )2
5,2
1(Q
PQ M ),( yx 2
2
5
,2
2
1 t
y
s
x
+
=
+
=
2
52,2
12 −=−= ytxs
P C
2)2
12(2
52 −=− xy 8
112 +−= xxy P L A
B 22
121 <−<− x 4
5
4
1 <<− x M
8
112 +−= xxy 4
5
4
1 <<− x
(2)曲线 ,
即圆 : ,其圆心坐标为 ,半径
由图可知,当 时,曲线 与点 有公共
点;
当 时,要使曲线 与点 有公共点,只需圆
心 到直线 的距离 ,得 ,则 的
最小值为 .
(2009·安徽理)(本小题满分 13 分)
点 在椭圆 上,
直线 与直线 垂直,O 为坐标原点,直线 OP 的倾斜角为 ,直线 的倾
斜角为 .
(I)证明: 点 是椭圆 与直线 的唯一交点;
(II)证明: 构成等比数列.
【解析】解:本小题主要考查直线和椭圆的标准方程和参数方程,直线和曲线的几何性
质,等比数列等基础知识。考查综合运用知识分析问题、解决问题的能力。本小题满分 13
分。
2 2 2 51: 2 4 025G x ax y y a− + − + + =
E 25
49)2()( 22 =−+− yax )2,(aE 5
7=r
20 ≤≤ a 2 2 2 51: 2 4 025G x ax y y a− + − + + = D
0 > 0 0cos , sin ,0 .2x a y b
πβ β β= = < <
2l 0 0
1 2 2: 1x yl x ya b
+ = α 2l
γ
P
2 2
2 2 1x y
a b
+ = 1l
tan ,tan ,tanα β γ
因此,方程组 有唯一解 ,即直线 与椭圆有唯一交点 P.
(方法二)显然 P 是椭圆与 的交点,若 Q 是椭圆与 的
交点,代入 的方程 ,得
即 故 P 与 Q 重合。
(II) 的斜率为 的斜率为
由此得 构成等比数列。
(2009·福建理 19)(本小题满分 13 分)
已知 A,B 分别为曲线 C: + =1(y 0,a>0)与 x 轴
的左、右两个交点,直线 过点 B,且与 轴垂直,S 为 上
异于点 B 的一点,连结 AS 交曲线 C 于点 T.
(1)若曲线 C 为半圆,点 T 为圆弧 的三等分点,试求出
点 S 的坐标;
(II)如图,点 M 是以 SB 为直径的圆与线段 TB 的交点,试问:是否存在 ,使得
O,M,S 三点共线?若存在,求出 a 的值,若不存在,请说明理由。
【解析】解法一:
2 2
2 2
0 0
2 2
1
1
x y
a b
x yx ya b
+ =
+ =
0
0
x x
y y
=
= 1l
1l 1 1 1( cos , sin ),0 2a bβ β β π≤ < 1l
1l cos sin 1x ya b
β β+ = 1 1cos cos sin sin 1,β β β β+ =
1 1cos( ) 1, ,β β β β− = =
0
0
tan tan ,y b
x a
α β= = 1l
2
0
2
0
,x b
y a
− 2l
2
0
2
0
tan tan ,y a a
x b b
γ β= =
2tan tan tan 0,α γ β= ≠ tan ,tan ,tanα β γ
2
2
x
a
2y ≥
l x l
AB
a
由
由 ,可得 即
经检验,当 时,O,M,S 三点共线. 故存在 ,使得 O,M,S 三点共线.
解法二:
(Ⅰ)同解法一.
(Ⅱ)假设存在 a,使得 O,M,S 三点共线.
由于点 M 在以 SO 为直径的圆上,故 .
显然,直线 AS 的斜率 k 存在且 K>0,可设直线 AS 的方程为
由
2
2
2 2 2 2 2 4 2 22 1 (1 ) 2 0
( )
x y a k x a k x a k aa
y k x a
+ = + + + − =
= +
得
BT OS⊥
2 2 2 2
2
2 4 01 2
a k a kBT OS a k
− +⋅ = =+
2 2 2 22 4 0a k a k− + =
0, 0, 2k a a> > ∴ =
2a = 2a =
SM BT⊥
( )y k x a= +
2
2
2 2 2 2 2 2 2 22 1 (1 ) 2 0
( )
x y a b x a k x a k aa
y k x a
+ = + + + − =
= +
得
设点 ,则有
故
由 所直线 SM 的方程为
O,S,M 三点共线当且仅当 O 在直线 SM 上,即 .
故存在 ,使得 O,M,S 三点共线.
(2009·辽宁理)(本小题满分 12 分)
已知,椭圆 C 过点 A ,两个焦点为(-1,0),(1,0)。
(1)求椭圆 C 的方程;
(2)E,F 是椭圆 C 上的两个动点,如果直线 AE 的斜率与 AF 的斜率互为相反
数,证明直线 EF 的斜率为定值,并求出这个定值。
【解析】解:
( , )T TT x y
4 2 2
2 2( ) .1T
a k ax a a k
−⋅ − = +
2 2 2 2
2 2 2 2 2 2 2 2
2 2, ( ) ( ).1 1 1T T T
a a k ak a a k akx y k x a Ta a k a k a k a k
− −= = + = ⋅+ + + +从而 亦即
2
2
1( ,0), ,T
BT SM
T
yB a k k a kx a a k
∴ = = − =− 故
( )
x a
y k x a
=
= +
得S( a, 2ak) , 22 ( )y ak a k x a− = −
22 ( )ak a k a= −
0, 0, 2a K a> > ∴ =
2a =
3(1, )2
(2009·宁夏海南理)(本小题满分 12 分)
已知椭圆 C 的中心为直角坐标系 xOy 的原点,焦点在 s 轴上,它的一个顶点到两个
焦点的距离分别是 7 和 1.
(Ⅰ)求椭圆 C 的方程;
(Ⅱ)若 P 为椭圆 C 上的动点,M 为过 P 且垂直于 x 轴的直线上的点, =λ,求
点 M 的轨迹方程,并说明轨迹是什么曲线。
【解析】解:(Ⅰ)设椭圆长半轴长及半焦距分别为 ,由已知得
,
所以椭圆 的标准方程为
(Ⅱ)设 ,其中 。由已知 及点 在椭圆 上可得
。
整理得 ,其中 。
(i) 时。化简得
所以点 的轨迹方程为 ,轨迹是两条平行于 轴的线段。
(ii) 时,方程变形为 ,其中
OP
OM
a c,
1 , 4, 37
a c a ca c
− = = = + =
解得
C
2 2
116 7
x y+ =
( , )M x y [ ]4,4x∈ −
2
2
2
OP
OM
λ= P C
2
2
2 2
9 112
16( )
x
x y
λ+ =+
2 2 2 2(16 9) 16 112x yλ λ− + = [ ]4,4x∈ −
3
4
λ = 29 112y =
M 4 7 ( 4 4)3y x= ± − ≤ ≤ x
3
4
λ ≠
2 2
2 2
1112 112
16 9 16
x y
λ λ
+ =
−
[ ]4,4x∈ −
当 时,点 的轨迹为中心在原点、实轴在 轴上的双曲线满足
的部分。
当 时,点 的轨迹为中心在原点、长轴在 轴上的椭圆满足 的部
分;
当 时,点 的轨迹为中心在原点、长轴在 轴上的椭圆;
(2009·天津理)(本小题满分 14 分)
以 知 椭 圆 的 两 个 焦 点 分 别 为
, 过 点 的 直 线 与 椭 圆 相 交 与 两 点 , 且
。
(1) 求椭圆的离心率;
(2) 求直线 AB 的斜率;
(3) 设 点 C 与 点 A 关 于 坐 标 原 点 对 称 , 直 线 上 有 一 点
在 的外接圆上,求 的值
【解析】(1)解:由 // 且 ,得 ,从而
整理,得 ,故离心率
30 4
λ< < M y 4 4x− ≤ ≤
3 14
λ< < M x 4 4x− ≤ ≤
1λ ≥ M x
2 2
2 2 1( 0)x y a ba b
+ = > >
1 2( ,0) ( ,0)( 0)F c F c c− >和
2
( ,0)aE c ,A B
1 2 1 2/ / , 2F A F B F A F B=
2F B
( , )( 0)H m n m ≠ ∆ 1AFC n
m
1FA 2F B 1 2FA 2 F B= 2 2
1 1
EF F B 1
EF FA 2
= =
2
2
a
1
a 2
cc
cc
−
=
+
2 23a c= 3
3
ce a
= =
将 代入②中,解得 .
(III)解法一:由(II)可知
当 时,得 ,由已知得 .
线段 的垂直平分线 l 的方程为 直线 l 与 x 轴
的 交 点 是 外 接 圆 的 圆 心 , 因 此 外 接 圆 的 方 程 为
.
直线 的方程为 ,于是点 H(m,n)的坐标满足方程组
, 由 解得 故
当 时,同理可得 .
1 2,x x 2
3k = ±
1 2
30, 2
cx x= =
2
3k = − (0, 2 )A c (0, 2 )C c−
1AF 2 2
2 2 2
cy c x − = − +
,02
c
1AFC∆
2 2
2x 2 2
c cy c − + = +
2F B 2( )y x c= −
2 2
2 9
2 4
2( )
c cm n
n m c
− + =
= −
0,m ≠
5
3
2 2
3
m c
n c
=
=
2 2
5
n
m
=
2
3k = 2 2
5
n
m
= −
解法二:由(II)可知
当 时,得 ,由已知得
由椭圆的对称性可知 B, ,C 三点共线,因为点 H(m,n)在 的外接圆上,
且 ,所以四边形 为等腰梯形.
由直线 的方程为 ,知点 H 的坐标为 .
因 为 , 所 以 , 解 得 m=c ( 舍 ),或
.
则 ,所以 .
当 时同理可得
【2008 年高考真题】
(2008·海南、宁夏理)已知点 P 在抛物线 上,那么点 P 到点 的距离
与点 P 到抛物线焦点距离之和取得最小值时,点 P 的坐标为( )
A. B. C. D.
解 析 : 点 P 到 抛 物 线 焦 点 距 离 等 于 点 P 到 抛 物 线 准 线 距 离 , 如 图
,故最小值在 三点共线时取得,此时 的纵坐标都是 ,
所以选 A。(点 坐标为 )
答案:A
1 2
30, 2
cx x= =
2
3k = − (0, 2 )A c (0, 2 )C c−
2F 1AFC∆
1 2//F A F B 1AFCH
2F B 2( )y x c= − ( , 2 2 )m m c−
1AH CF= 2 2 2( 2 2 2 )m m c c a+ − − =
5
3m c=
2 2
3n c= 2 2
5
n
m
=
2
3k = n 2 2
5m
= −
2 4y x= (2 1)Q −,
1 14
− , 1 14
, (1 2), (1 2)−,
PF PQ PS PQ+ = + , ,S P Q ,P Q 1−
P 1( , 1)4
−
(2008·山东理)设椭圆 C1 的离心率为 ,焦点在 X 轴上且长轴长为 26.若曲线 C2 上
的点到椭圆 C1 的两个焦点的距离的差的绝对值等于 8,则曲线 C2 的标准方程为
(A) (B)
(C) (D)
解析:本题考查椭圆、双曲线的标准方程。对于椭圆 , 曲线 为双曲
最短弦为
答案:B
(2008·广东)经过圆 的圆心 ,且与直线 垂直的直线方程
是 .
解析:易知点 C 为 ,而直线与 垂直,我们设待求的直线的方程为
,将点 C 的坐标代入马上就能求出参数 的值为 ,故待求的直线的方程为
。
答案:
( 2008· 江 苏 ) 在 平 面 直 角 坐 标 系 中 , 设 三 角 形 ABC 的 顶 点 坐 标 分 别 为
,点 在线段 OA 上(异于端点),设 均为非零实数,
直 线 分 别 交 于 点 E , F , 一 同 学 已 正 确 算 出 的 方 程 :
13
5
134 2
2
2
2
=− yx 1513 2
2
2
2
=− yx
143 2
2
2
2
=− yx 11213 2
2
2
2
=− yx
1C 13, 5,a c= = 2C
10,AC = 2 22 5 1 4 6,BD = − = 1 20 6.2S AC BD= ⋅ =
2 22 0x x y+ + = C 0x y+ =
( 1,0)− 0x y+ =
y x b= + b 1b =
1 0x y− + =
1 0x y− + =
(0, ), ( ,0), ( ,0)A a B b C c (0, )P p , , ,a b c p
,BP CP ,AC AB OE
,请你求 OF 的方程: 。
(2008·江苏)在平面直角坐标系中,椭圆 的焦距为 2,以 O 为圆心,
为半径的圆,过点 作圆的两切线互相垂直,则离心率 = ▲ 。
解析:本小题考查椭圆的基本量和直线与圆相切的位置关系。如图,切线 互相
垂直,又 ,所以 是等腰直角三角形,故 ,解得 。
答案:
(2008·海南、宁夏理)设双曲线 的右顶点为 A,右焦点为 F.过点 F 平行
双曲线的一条渐近线的直线与双曲线交于点 B,则△AFB 的面积为 .
解析:双曲线的右顶点坐标 ,右焦点坐标 ,设一条渐近线方程为 ,
建立方程组 ,得交点纵坐标 ,从而
答案:
1 1 1 1 0x yb c p a
− + − =
2 2
2 2 1( 0)x y a ba b
+ = > >
a
2( ,0)a
c e
,PA PB
OA PA⊥ OAP∆
2
2a ac
= 2
2
ce a
= =
2
2
2 2
19 16
x y− =
(3,0)A (5,0)F 4
3y x=
2 2
4 ( 5)3
19 16
y x
x y
= −
− =
32
15y = − 1 32 3222 15 15AFBS = × × =
15
32
(2008·广东)设 ,椭圆方程为 ,抛物线方程为 .如图
所示,过点 作 轴的平行线,与抛物线在第一象限的交点为 ,已知抛物线在
点 的切线经过椭圆的右焦点 .
(1)求满足条件的椭圆方程和抛物线方程;
(2)设 分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点 ,使得
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这
些点的坐标).
解析:(1)由 得 ,
当 得 , G 点的坐标为 ,
, ,
过点 G 的切线方程为 即 ,
令 得 , 点的坐标为 ,由椭圆方程得 点的坐标为 ,
即 ,即椭圆和抛物线的方程分别为 和 ;
( 2 ) 过 作 轴 的 垂 线 与 抛 物 线 只 有 一 个 交 点 , 以 为 直 角 的
只有一个,
0b >
2 2
2 2 12
x y
b b
+ = 2 8( )x y b= −
(0 2)F b +, x G
G 1F
A B, P
ABP△
2 8( )x y b= − 21
8y x b= +
2y b= + 4x = ± ∴ (4, 2)b +
1' 4y x= 4'| 1xy = =
( 2) 4y b x− + = − 2y x b= + −
0y = 2x b= − 1F∴ (2 ,0)b− 1F ( ,0)b
2 b b∴ − = 1b =
2
2 12
x y+ = 2 8( 1)x y= −
A x P ∴ PAB∠
Rt ABP∆
同理 以 为直角的 只有一个;
若以 为直角,则点 在以 为直径的圆上,而以 为直径的圆与抛物线
有两个交点。
所以以 为直角的 有两个;
因此抛物线上存在四个点使得 为直角三角形。
(2008·山东理)如图,设抛物线方程为 x2=2py(p>0),M 为 直线 y=-2p 上任意一点,过
M 引抛物线的切线,切点分别为 A,B.
(Ⅰ)求证:A,M,B 三点的横坐标成等差数列;
(Ⅱ)已知当 M 点的坐标为(2,-2p)时, ,求此时抛物线的方程;
(Ⅲ)是否存在点 M,使得点 C 关于直线 AB 的对称点 D 在抛物线 上,
其中,点 C 满足 (O 为坐标原点).若存在,求出所有适合题意的点 M 的
坐标;若不存在,请说明理由.
解析:(Ⅰ)证明:由题意设
∴ PBA∠ Rt ABP∆
APB∠ P AB AB
APB∠ Rt ABP∆
ABP∆
4 10AB =
2 2 ( 0)x py p= >
OC OA OB= +
2 2
1 2
1 2 1 2 0( , ), ( , ), , ( , 2 ).2 2
x xA x B x x x M x pp p
−<
由①、②得
因此 ,即
所以 A、M、B 三点的横坐标成等差数列.
(Ⅱ)解:由(Ⅰ)知,当 x0=2 时,
将其代入①、②并整理得:
所以 x1、x2 是方程 的两根,
因此
又
所以
2
1 2
1 2 0 ,2
x x x x x
+ = + −
2
1 2
0 2
x xx
+= 0 1 22 .x x x= +
2 2
1 14 4 0,x x p− − =
2 2
2 24 4 0,x x p− − =
2 24 4 0x x p− − =
2
1 2 1 24, 4 ,x x x x p+ = = −
2 2
2 1
01 2
2 1
2 2 ,2AB
x x
xx xp pk x x p p
− += = =−
2 .ABk p
=
(Ⅲ)解:设 D(x3,y3),由题意得 C(x1+ x2, y1+ y2),
则 CD 的中点坐标为
设直线 AB 的方程为
由点 Q 在直线 AB 上,并注意到点 也在直线 AB 上,
代入得
若 D(x3,y3)在抛物线上,则
因此 x3=0 或 x3=2x0.
即 D(0,0)或
(1)当 x0=0 时,则 ,此时,点 M(0,-2p)适合题意.
(2)当 ,对于 D(0,0),此时
又 AB⊥CD,
所以
即 矛盾.
对于 因为 此时直线 CD 平行于 y 轴,
1 2 3 1 2 3( , ),2 2
x x x y y yQ
+ + + +
0
1 1( ),xy y x xp
− = −
1 2 1 2( , )2 2
x x y y+ +
0
3 3.xy xp
=
2
3 3 0 32 2 ,x py x x= =
2
0
0
2(2 , ).xD x p
1 2 02 0x x x+ = =
0 0x ≠
2 2
1 2
2 2 2 2
1 2 1 2
0
0 0
2(2 , ), ,2 2 4CD
x x
x x x xpC x kp x px
+
+ += =
0 ,AB
xk p
=
2 2 2 2
0 1 2 1 2
2
0
1,4 4AB CD
x x x x xk k p px p
+ += = = −
2 2 2
1 2 4 ,x x p+ = −
2
0
0
2(2 , ),xD x p
2 2
1 2
0(2 , ),2
x xC x p
+
又
(2008 山东文)已知曲线 所围成的封闭图形的面积为 ,
曲线 的内切圆半径为 .记 为以曲线 与坐标轴的交点为顶点的椭圆.
(Ⅰ)求椭圆 的标准方程;
(Ⅱ)设 是过椭圆 中心的任意弦, 是线段 的垂直平分线. 是 上异于
椭圆中心的点.
(1)若 ( 为坐标原点),当点 在椭圆 上运动时,求点 的轨迹
方程;
(2)若 是 与椭圆 的交点,求 的面积的最小值.
解析:(Ⅰ)由题意得
又 ,
解得 , .
因此所求椭圆的标准方程为 .
( Ⅱ )( 1 ) 假 设 所 在 的 直 线 斜 率 存 在 且 不 为 零 , 设 所 在 直 线 方 程 为
,
.
0 0,AB
xk p
= ≠
1 1( 0)x yC a ba b
+ = > >: 4 5
1C 2 5
3 2C 1C
2C
AB 2C l AB M l
MO OAλ= O A 2C M
M l 2C AMB△
2 2
2 4 5
2 5
3
ab
ab
a b
=
= +
,
.
0a b> >
2 5a = 2 4b =
2 2
15 4
x y+ =
AB AB
( 0)y kx k= ≠
( )A AA x y,
解方程组 得 , ,
所以 .
设 ,由题意知 ,
所以 ,即 ,
因为 是 的垂直平分线,
所以直线 的方程为 ,
即 ,
因此 ,
又 ,
所以 ,
故 .
又当 或不存在时,上式仍然成立.
综上所述, 的轨迹方程为 .
(2)当 存在且 时,由(1)得 , ,
2 2
15 4
x y
y kx
+ =
=
,
,
2
2
20
4 5Ax k
= +
2
2
2
20
4 5A
ky k
= +
2 2
2 2 2
2 2 2
20 20 20(1 )
4 5 4 5 4 5A A
k kOA x y k k k
+= + = + =+ + +
( )M x y, ( 0)MO OAλ λ= ≠
2 22MO OAλ=
2
2 2 2
2
20(1 )
4 5
kx y k
λ ++ = +
l AB
l 1y xk
= −
xk y
= −
2
2 2 2
2 2 2 2
2 2 2
2
20 1
20( )
4 54 5
x
y x yx y x y x
y
λ λ
+ + + = = ++
2 2 0x y+ ≠
2 2 25 4 20x y λ+ =
2 2
2
4 5
x y λ+ =
0k =
M
2 2
2 ( 0)4 5
x y λ λ+ = ≠
k 0k ≠ 2
2
20
4 5Ax k
= +
2
2
2
20
4 5A
ky k
= +
.
解法一:由于
,
当且仅当 时等号成立,即 时等号成立,此时 面积的最
小值是 .
当 , .
当 不存在时, .
综上所述, 的面积的最小值为 .
解法二:因为 ,
又 , ,
2
2
2
20(1 )
5 4
kOM k
+= +
2 22 1
4AMBS AB OM= △
2 2
2 2
1 80(1 ) 20(1 )
4 4 5 5 4
k k
k k
+ += × ×+ +
2 2
2 2
400(1 )
(4 5 )(5 4 )
k
k k
+= + +
2 2
22 2
400(1 )
4 5 5 4
2
k
k k
+
+ + +
≥
22 2
2 2
1600(1 ) 40
81(1 ) 9
k
k
+ = = +
2 24 5 5 4k k+ = + 1k = ± AMB△
40
9AMBS =△
0k = 1 402 5 2 2 52 9AMBS = × × = >△
k 1 405 4 2 52 9AMBS = × × = >△
AMB△ 40
9
2 2 2 2
2 2
1 1 1 1
20(1 ) 20(1 )
4 5 5 4
k kOA OM
k k
+ = ++ +
+ +
2 2
2
4 5 5 4 9
20(1 ) 20
k k
k
+ + += =+
2 2
1 1 2
OA OMOA OM
+
≥ 40
9OA OM ≥
(2008 海南、宁夏理)在直角坐标系 xOy 中,椭圆 C1: =1(a>b>0)的左、
右焦点分别为 F1,F2.F2 也是抛物线 C2: 的焦点,点 M 为 C1 与 C2 在第一象限的
交点,且|MF2|= .
(Ⅰ)求 C1 的方程;
(Ⅱ)平面上的点 N 满足 ,直线 l∥MN,且与 C1 交于 A,B 两点,
若 ,求直线 l 的方程.
解析:(Ⅰ)由 : 知 .
设 , 在 上 , 因 为 , 所 以 , 得 ,
.
在 上,且椭圆 的半焦距 ,于是
消去 并整理得 , 解得 ( 不合题意,舍去).
故椭圆 的方程为 .
(Ⅱ)由 知四边形 是平行四边形,其中心为坐标原点 ,
因为 ,所以 与 的斜率相同,
2
2
2
2
b
y
a
x +
2 4y x=
3
5
21 MFMFMN +=
0OA OB =
2C 2 4y x= 2 (1 0)F ,
1 1( )M x y, M 2C 2
5
3MF = 1
51 3x + = 1
2
3x =
1
2 6
3y =
M 1C 1C 1c = 2 2
2 2
4 8 19 3
1.
a b
b a
+ =
= −
,
2b 4 29 37 4 0a a− + = 2a = 1
3a =
1C
2 2
14 3
x y+ =
1 2MF MF MN+ =
1 2MF NF O
l MN∥ l OM
故 的斜率 .设 的方程为 .l
2 6
3 62
3
k = = l 6( )y x m= −