2012高中数学人教A版必修3综合测试题及答案 10

2012高中数学人教A版必修3综合测试题及答案 10

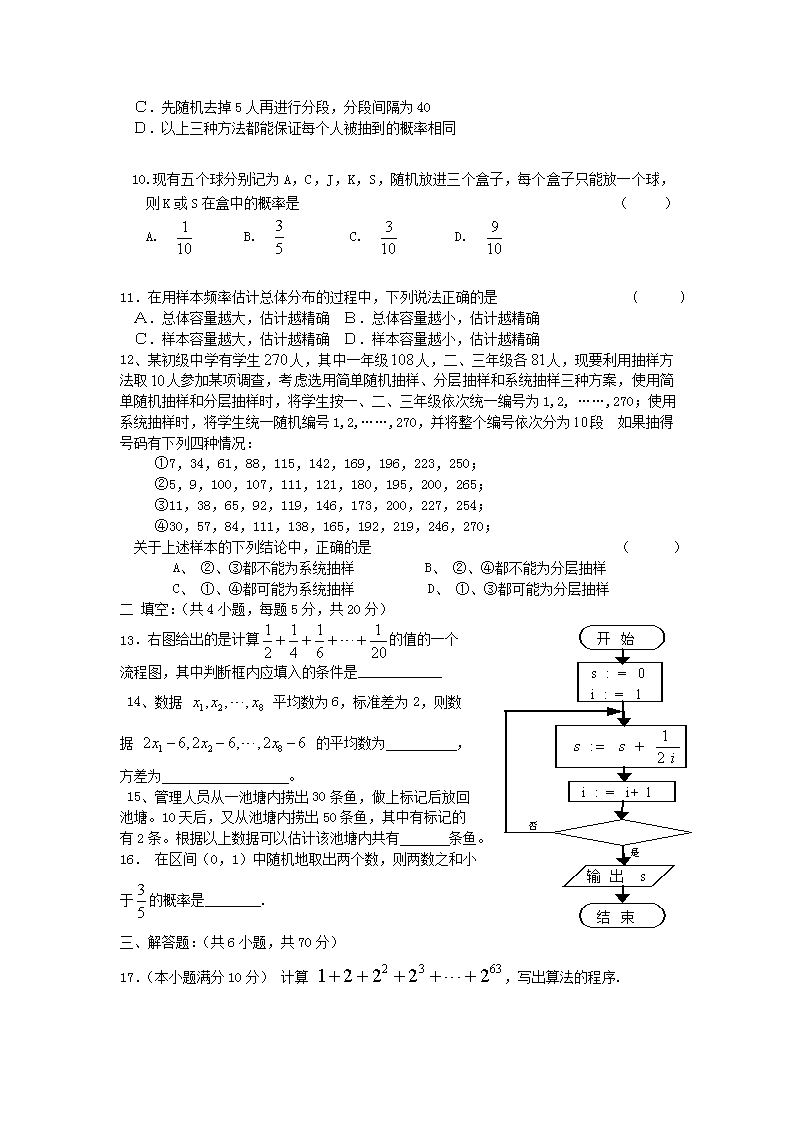
必修3综合模块测试10（人教A版必修3）‎ 一、选择：（共12小题，每题5分，共60分）‎ ‎1. 算法的三种基本结构是 ( )‎ ‎ A. 顺序结构、模块结构、条件结构 B. 顺序结构、循环结构、模块结构 ‎ C. 顺序结构、条件结构、循环结构 D. 模块结构、条件结构、循环结构 ‎2下列说法正确的是 （ ）‎ A.　任何事件的概率总是在（0，1）之间 ‎ B.　频率是客观存在的，与试验次数无关 C.　随着试验次数的增加，频率一般会越来越接近概率 D.　概率是随机的，在试验前不能确定 ‎3．用二分法求方程的近似根的算法中要用哪种算法结构 （ ）‎ A．顺序结构 B．条件结构 C．循环结构 D．以上都用 ‎4．若=，则事件A与B的关系是 （ ）‎ s=0‎ i=2‎ Do s=s+i i= i+2‎ Loop until ‎ Print s End 第5题 ‎ A 互斥不对立 B 对立不互斥 C互斥且对立 D以上都不对 ‎5．有下面的程序，运行该程序，要使输出的结果是30，‎ 在处 应添加的条件是 （ ）‎ A. i>12 B. i>‎10 C. i=14 D. i=10‎ ‎6．用“辗转相除法”求得459和357的最大公约数是： （ ）‎ A．3 B．‎9 C．17 D．51‎ ‎7．线性回归方程所表示的直线必经过点 （ ） ‎ A．（0，0） B．（） C．（） D．（）‎ ‎8．下面有三个游戏规则，袋子中分别装有球，从袋中无放回地取球，问其中不公平的游戏是 ( ) ‎ 游戏1‎ 游戏2‎ 游戏3‎ ‎3个黑球和一个白球 一个黑球和一个白球 ‎2个黑球和2个白球 取1个球，再取1个球 取1个球 取1个球，再取1个球 取出的两个球同色→甲胜 取出的球是黑球→甲胜 取出的两个球同色→甲胜 取出的两个球不同色→乙胜 取出的球是白球→乙胜 取出的两个球不同色→乙胜 A． 游戏1和游戏3 B．游戏‎1 C．游戏2 D．游戏3‎ ‎9．为了了解2405名学生对学校某项教改试验的意见，打算从中抽取一个容量为60的样本，若用系统抽样，则下列说法正确的是 （ 　）‎ Ａ．直接进行分段，分段间隔为40，然后把剩余5人放到其中的一段　　‎ Ｂ．直接分段间隔为40，把剩余的5人单独放到一段 Ｃ．先随机去掉5人再进行分段，分段间隔为40‎ Ｄ．以上三种方法都能保证每个人被抽到的概率相同 ‎10.现有五个球分别记为A，C，J，K，S，随机放进三个盒子，每个盒子只能放一个球，则K或S在盒中的概率是 （ ）‎ A.　 　　　B.　 　　 C.　　　　 D.　‎ ‎11．在用样本频率估计总体分布的过程中，下列说法正确的是 ( )‎ Ａ．总体容量越大，估计越精确 Ｂ．总体容量越小，估计越精确 Ｃ．样本容量越大，估计越精确 Ｄ．样本容量越小，估计越精确 ‎12、某初级中学有学生人，其中一年级人，二、三年级各人，现要利用抽样方法取人参加某项调查，考虑选用简单随机抽样、分层抽样和系统抽样三种方案，使用简单随机抽样和分层抽样时，将学生按一、二、三年级依次统一编号为1,2, ……,270；使用系统抽样时，将学生统一随机编号1,2, ……,270，并将整个编号依次分为段 如果抽得号码有下列四种情况：‎ ‎①7，34，61，88，115，142，169，196，223，250；‎ ‎②5，9，100，107，111，121，180，195，200，265；‎ ‎③11，38，65，92，119，146，173，200，227，254；‎ ‎④30，57，84，111，138，165，192，219，246，270；‎ 关于上述样本的下列结论中，正确的是 （ ）‎ A、 ②、③都不能为系统抽样 B、 ②、④都不能为分层抽样 C、 ①、④都可能为系统抽样 D、 ①、③都可能为分层抽样 二 填空：（共4小题，每题5分，共20分）‎ ‎13．右图给出的是计算的值的一个 流程图，其中判断框内应填入的条件是____________ ‎ ‎ 14、数据 平均数为6，标准差为2，则数 据 的平均数为 ，‎ 方差为 。‎ ‎ 15、管理人员从一池塘内捞出30条鱼，做上标记后放回 池塘。10天后，又从池塘内捞出50条鱼，其中有标记的 有2条。根据以上数据可以估计该池塘内共有 条鱼。‎ ‎16． 在区间（0，1）中随机地取出两个数，则两数之和小 于的概率是________.‎ 三、解答题：（共6小题，共70分）‎ ‎17．（本小题满分10分） 计算 ，写出算法的程序.‎ ‎18．（本小题满分12分）下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量(吨)与相应的生产能耗 (吨标准煤)的几组对照数据 ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ (1)请画出上表数据的散点图；‎ ‎ (2)请根据上表提供的数据，用最小二乘法求出关于的线性回归方程；‎ ‎ (3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤．试根据(2)求出的线性回归方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?‎ ‎ (参考数值：，‎ ‎（，）‎ ‎19. （本小题满分12分）假设有5个条件很类似的女孩，把她们分别记为A，C，J，K，S。她们应聘秘书工作，但只有3个秘书职位，因此5人中仅有三人被录用。如果5人被录用的机会均等，分别计算下列事情的概率有多大？‎ ‎（1）女孩K得到一个职位 ‎ （2）女孩K和S各得到一个职位 ‎（3）女孩K或S得到一个职位 ‎20．（本小题满分12分）某次运动会甲、乙两名射击运动员成绩如下：‎ 甲：9.4，8.7，7.5，8.4，10.1，10.5，10.7，7.2，7.8，10.8；‎ 乙：9.1，8.7，7.1，9.8，9.7，8.5，10.1，9.2，10.1，9.1；‎ （1） 用茎叶图表示甲，乙两个成绩；‎ （2） 分别计算两个样本的平均数和标准差s，并根据计算结果估计哪位运动员的成绩比较稳定。‎ ‎21．（本小题满分12分）假设你家订了一份报纸，送报人可能在早上6点—8点之间把报纸送到你家，你每天离家去工作的时间在早上7点—9点之间 ，求你离家前不能看到报纸（称事件A）的概率是多少？‎ ‎22. （本小题满分12分）有一个容量为50的样本，数据的 分组及各组的频数如下 ‎ 3; 8； 9； 11； 10；‎ ‎ 5； 4.‎ ‎（1）列频率分布表 ‎（2）画出频率分布直方图 ‎（3）根据频率分布直方图估计数据落在的概率是多少 ‎ 参考答案 一、选择：（题每题5分，共60分）‎ ‎1C‎ ‎2C 3D 4D 5B 6D 7D 8D ‎9C 10D ‎11C 12D 二 填空：（每题5分，共20分）‎ ‎13 . i＞10 14 . 6 16 15.750 16. ‎ 三、解答题： 17．（10分）.‎ i=1‎ S=1‎ WHILE i <= 63‎ S=s+2^i i=i+1‎ WEND PRINT s END 或 i=1‎ S=1‎ DO ‎ S=s+2^i i=i+1‎ LOOP UNTIL i >63‎ PRINT s END ‎18．（ 12 分）‎ ‎.解：（1） ‎ ‎ . 4分 ‎(2)=32．5+43+54+64．5=66．5‎ ‎==4．5‎ ‎==3．5‎ ‎=+++=86‎ 故线性回归方程为y=0．7x+0．35 8分 ‎(3)根据回归方程的预测，现在生产100吨产品消耗的标准煤的数量为0．7100+0．35=70．35‎ 故耗能减少了90-70．35=19．65(吨) 12分 ‎19.（12分）‎ 解（1）P= . 4分 ‎（2）P= . 8分 ‎（3）P= . 12分 （1） ‎20．（本小题满分12）‎ 解：（1）如图所示，茎表示成绩的整数环数，叶表示小数点后的数字。‎ ‎ 甲 乙 ‎8 2 5 7 1‎ ‎ 4 7 8 7 5‎ ‎ 4 9 1 8 7 2 1‎ ‎8 7 5 1 10 1 1‎ ‎ 4分 ‎（2）解：（3）甲＝×（9.4+8.7+7.5+8.4+10.1+10.5+10.7+7.2+7.8+10.8）=9.11‎ S甲＝＝1.3‎ 乙＝×（9.1+8.7+7.1+9.8+9.7+8.5+10.1+9.2+10.1+9.1）=9.11＝9.14‎ S乙＝＝0.9‎ 因为S甲>S乙，这说明了甲运动员的波动大于乙运动员的波动，‎ 所以我们估计，乙运动员比较稳定。 12分 ‎21．（12分）解：如图，设送报人到达的时间为X，小王离家去工作的时间为Y。‎ ‎（X，Y）可以看成平面中的点，试验的全部结果所构成的区域为一个正方形区域，面积为SΩ=4， 4分 事件A表示小王离家前不能看到报纸，所构成的区域为A={（X，Y）/ 即图中的阴影部分，面积为SA=0.5。 8分 这是一个几何概型，所以P（A）=SA/SΩ=0.5/4=0.125。‎ 答：小王离家前不能看到报纸的概率是0.125。 12分 Y X、、X ‎9‎ ‎7‎ ‎6 8‎ ‎22. ‎ 组　别 频数 频率 ‎ ‎ ‎3‎ ‎0.06‎ ‎8‎ ‎0.16‎ ‎9‎ ‎0.18‎ ‎11‎ ‎0.22‎ ‎10‎ ‎0.20‎ ‎5‎ ‎0.10‎ ‎4‎ ‎0.08‎ 合　计 ‎50‎ ‎1.00‎ ‎ 4分 ‎（2） ‎ ‎ ‎ ‎ 频率/组距 ‎ 0.073‎ ‎ 0.067 --------------------------------‎ ‎ 0.06 0 --------------------‎ ‎ ‎ ‎ 0.053 ---------------‎ ‎ 0.033 -----------------------‎ ‎0.026 -------------‎ ‎0.02 0--------- ‎ ‎0 12.5 15.5 18.5 21.5 24.5 27.5 30.5 33.5‎ ‎ 8分 ‎（3）P=0.56 12分 ‎