2018届二轮复习7.1二元一次不等式(组)与简单的线性规划问题（2）教案（全国通用）

2018届二轮复习7.1二元一次不等式(组)与简单的线性规划问题（2）教案（全国通用）

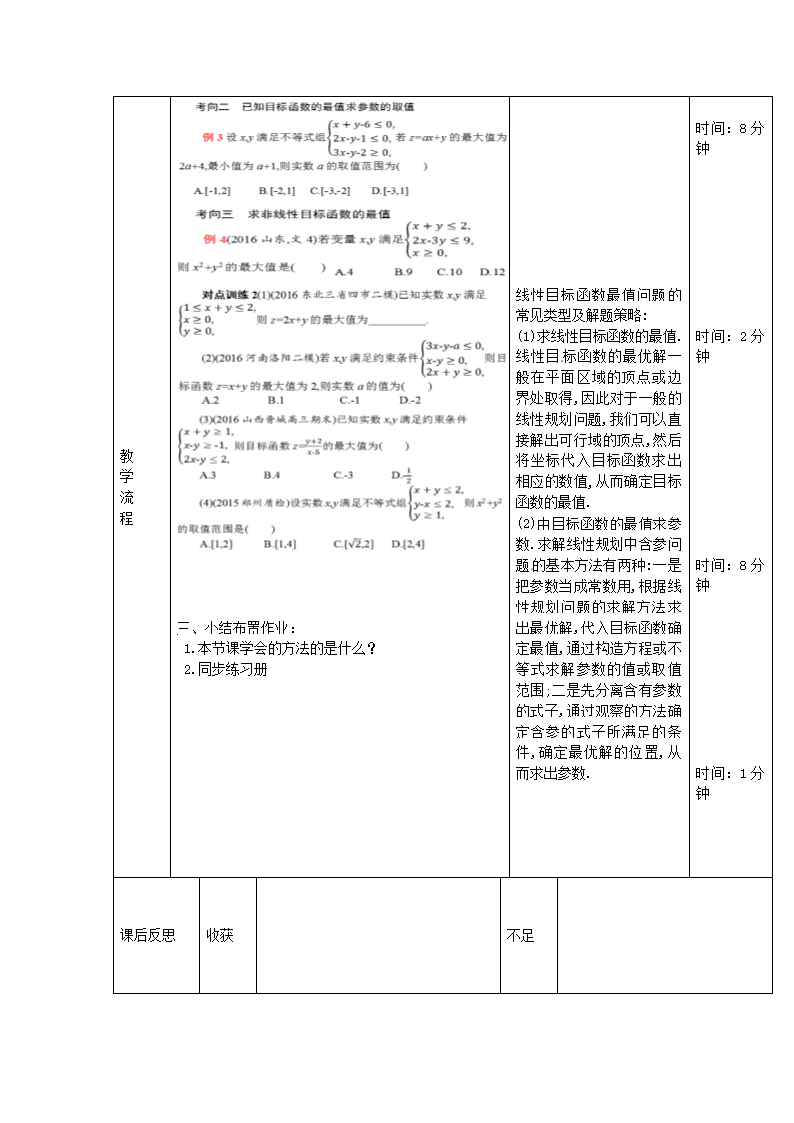
第5周 9月18日—— 9月22日 第 4课时 授课人 授课时间 ‎9、21‎ 课 型 复习课 课 题 ‎ 7.1二元一次不等式(组)与简单的线性规划问题 ‎（2）‎ 主备人 ‎ ‎ 教学目标 ‎（学习目标）‎ 巩固复习二元一次不等式(组)与简单的线性规划问题知识点。‎ 教材分析 教学重点 二元一次不等式(组)与简单的线性规划问题。‎ 教学难点 二元一次不等式(组)与简单的线性规划问题。‎ 疑难预设 计算公式的记忆与运用。[来源:学科网ZXXK]‎ 模式与方法 讲练结合 教 学 流[来源:学科网]‎ 程[来源:学科网]‎ 教 学 内 容 师生活动及时间分配 个案补充 解题心得确定二元一次不等式(组)表示的平面区域的方法:‎ ‎(1)“直线定界,特殊点定域”,即先作直线,再取特殊点并代入不等式组.若满足不等式组,则不等式(组)表示的平面区域为直线与特殊点同侧的那部分区域;否则就对应特殊点异侧的平面区域.‎ ‎(2)若不等式带等号,则边界为实线;若不等式不带等号,则边界为虚线.‎ 教师引领学生回顾复习 二元一次不等式(组)与简单的线性规划问题知识点。‎ 教师引导学生记忆公式。‎ 时间安排：10分钟 时间：6分钟 时间：10分钟 教 学 内 容 师生活动及时间分配 个案补充 教 学 流 程 三、小结布置作业：‎ ‎ 1.本节课学会的方法的是什么？‎ ‎ 2.同步练习册 ‎ ‎ 线性目标函数最值问题的常见类型及解题策略:‎ ‎(1)求线性目标函数的最值.线性目标函数的最优解一般在平面区域的顶点或边界处取得,因此对于一般的线性规划问题,我们可以直接解出可行域的顶点,然后将坐标代入目标函数求出相应的数值,从而确定目标函数的最值.‎ ‎(2)由目标函数的最值求参数.求解线性规划中含参问题的基本方法有两种:一是把参数当成常数用,根据线性规划问题的求解方法求出最优解,代入目标函数确定最值,通过构造方程或不等式求解参数的值或取值范围;二是先分离含有参数的式子,通过观察的方法确定含参的式子所满足的条件,确定最优解的位置,从而求出参数.‎ 时间：8分钟 时间：2分钟 时间：8分钟 时间：1分钟 课后反思 收获 不足