- 2021-06-30 发布 |
- 37.5 KB |
- 13页


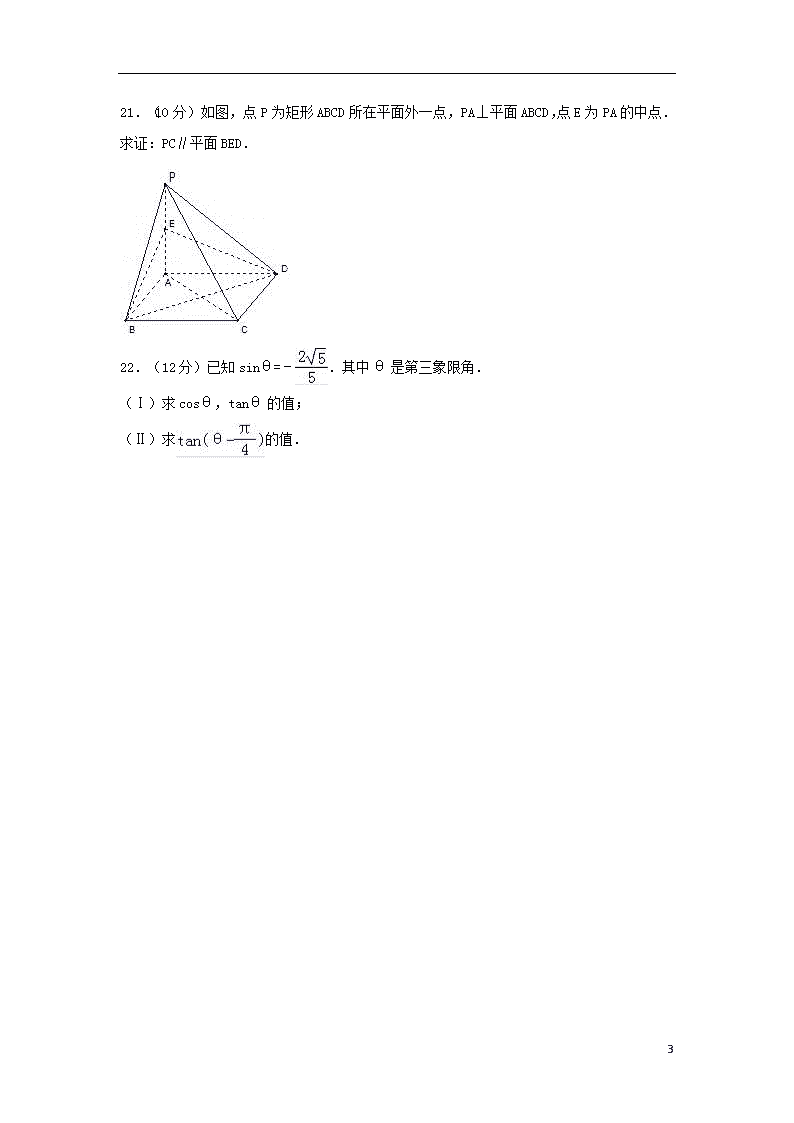
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019学年高二数学下学期期中试题 文 新版 新人教版
2019高二(下)期中数学试卷(文科) 一、选择题:本大题共14小题,每小题3分,共42分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.(3分)已知全集I={0,1,2,3,4},集合M={1,2,3},N={0,3],则(∁IM)∪N=( ) A.{0,3,4} B.{0} C.{0,1,2,3} D.{0,1,2,3,4} 2.(3分)sin240°=( ) A.﹣ B.﹣ C. D. 3.(3分)已知α∈[0,2π),与角终边相同的角是( ) A. B. C. D. 4.(3分)若sinα>0,且cosα<0,则角α是( ) A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限角 5.(3分)若角α的终边经过点P(﹣3,4),则tanα=( ) A. B. C. D. 6.(3分)函数的定义域为( ) A.(1,3) B.[1,3] C.(﹣∞,1)∪(3,+∞) D.(1,0)∪(0,+∞) 7.(3分)已知向量=(﹣1,2),=(1,0),那么向量的坐标是( ) A.(﹣4,2) B.(﹣4,﹣2) C.(4,2) D.(4,﹣2) 8.(3分)函数y=loga(x+2)+1的图象过定点( ) A.(﹣2,1) B.(2,1) C.(﹣1,1) D.(1,1) 9.(3分)已知向量,满足||=1,||=4且•=﹣2,则与的夹角为( ) A.150° B.120° C.60° D.30° 10.(3分)某商场出售三种品牌电脑,现存分别是60台、36台和24台,用分层抽样的方法从中抽取10台进行检测,这三种品牌的电脑依次应抽取的台数是( ) A.6,3,1 B.5,3,2 C.5,4,1 D.4,3,3 11.(3分)已知函数f(x)=,则f[f(2)]的值为( ) 13 A.﹣1 B.1 C.4 D.5 12.(3分)下列函数是偶函数的是( ) A.y=x B.y=2x2﹣3 C. D.y=x2,x∈[0,1] 13.(3分)下列四个图形是两个变x,y的散点图,其中具有线性相关关系的是( ) A. B. C. D. 14.(3分)设a=(),b=(),c=(),则a,b,c的大小关系是( ) A.a>c>b B.a>b>c C.c>a>b D.b>c>a 二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上. 15.(4分)已知集合A={x|x>1},B={x|x2﹣2x﹣3<0},则A∩B= . 16.(4分)sinα=3cosα,则tanα= . 17.(4分)已知向量=(﹣1,3),=(﹣3,x),若∥,则x= ;若,则x= . 18.(4分)函数f(x)=的定义域是 . 三、解答题共4小题,共42分.解答应写出文字说明,演算步骤或证明过程. 19.(10分)等差数列 {an}中,已知a2=3,a7=13 (1)求数列 {an}的通项公式; (2)求数列 {an}前10项的和S10. 20.(10分)求圆心C在直线y=2x上,且经过原点及点M(3,1)的圆C的方程. 13 21.(10分)如图,点P为矩形ABCD所在平面外一点,PA⊥平面ABCD,点E为PA的中点. 求证:PC∥平面BED. 22.(12分)已知sinθ=﹣.其中θ是第三象限角. (Ⅰ)求cosθ,tanθ的值; (Ⅱ)求的值. 13 2019高二(下)期中数学试卷(文科) 参考答案与试题解析 一、选择题:本大题共14小题,每小题3分,共42分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知全集I={0,1,2,3,4},集合M={1,2,3},N={0,3],则(∁IM)∪N=( ) A.{0,3,4} B.{0} C.{0,1,2,3} D.{0,1,2,3,4} 【考点】1H:交、并、补集的混合运算. 【分析】由全集I及M,求出M的补集,找出M补集与N的并集即可. 【解答】解:∵全集I={0,1,2,3,4},集合M={1,2,3},N={0,3], ∴∁IM={0,4}, 则(∁IM)∪N={0,3,4}, 故选:A. 【点评】此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键. 2.sin240°=( ) A.﹣ B.﹣ C. D. 【考点】GO:运用诱导公式化简求值. 【分析】运用诱导公式即可化简求值. 【解答】解:sin240°=sin(180°+60°)=﹣sin60°=﹣. 故选:A. 【点评】本题主要考察了运用诱导公式化简求值,属于基础题. 3.已知α∈[0,2π),与角终边相同的角是( ) A. B. C. D. 【考点】G2:终边相同的角. 【分析】写出与终边相同的角的集合{α|α=+2kπ,k∈Z},取k=1得答案. 13 【解答】解:∵与终边相同的角的集合为{α|α=+2kπ,k∈Z}. ∴取k=1时,α=∈[0,2π], 故选:D. 【点评】本题考查了终边相同的角的集合的写法,是基础的会考题型. 4.若sinα>0,且cosα<0,则角α是( ) A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限角 【考点】GC:三角函数值的符号. 【分析】直接由三角函数的象限符号取交集得答案. 【解答】解:由sinα>0,可得α为第一、第二及y轴正半轴上的角; 由cosα<0,可得α为第二、第三及x轴负半轴上的角. ∴取交集可得,α是第二象限角. 故选:B. 【点评】本题考查了三角函数的象限符号,是基础的会考题型. 5.若角α的终边经过点P(﹣3,4),则tanα=( ) A. B. C. D. 【考点】G9:任意角的三角函数的定义. 【分析】由三角函数的定义,tanα=,求出值即可 【解答】解:∵角α的终边经过点P(1,﹣2), ∴tanα==. 故选:C. 【点评】本题考查三角函数的定义tanα=,利用公式求值题. 6.函数的定义域为( ) A.(1,3) B.[1,3] C.(﹣∞,1)∪(3,+∞) D.(1,0)∪(0,+∞) 【考点】33:函数的定义域及其求法. 【分析】根据函数成立的条件即可求函数的定义域. 13 【解答】解:要使函数有意义,则, 即, 则1≤x≤3, 故函数的定义域为[1,3], 故选:B 【点评】本题主要考查函数的定义域求解,要求熟练掌握常见函数成立的条件. 7.已知向量=(﹣1,2),=(1,0),那么向量的坐标是( ) A.(﹣4,2) B.(﹣4,﹣2) C.(4,2) D.(4,﹣2) 【考点】9J:平面向量的坐标运算. 【分析】由已知中向量=(﹣1,2),=(1,0),根据数乘向量坐标运算公式,及向量减法坐标运算公式,可求出向量的坐标. 【解答】解:∵ =(﹣1,2),=(1,0), ∴向量=3(1,0)﹣(﹣1,2)=(4,﹣2) 故选D. 【点评】本题考查的知识点是平面向量的坐标运算,熟练掌握数乘向量坐标运算公式,及向量加法坐标运算公式,是解答本题的关键. 8.函数y=loga(x+2)+1的图象过定点( ) A.(﹣2,1) B.(2,1) C.(﹣1,1) D.(1,1) 【考点】4N:对数函数的图象与性质. 【分析】令x+2=1解得x=﹣1,y=1;从而写出即可. 【解答】解:令x+2=1得,x=﹣1,y=1; 故函数y=loga(x+2)+1的图象过定点(﹣1,1); 故选C. 【点评】本题考查了对数函数的性质应用,属于基础题. 9.已知向量,满足||=1,||=4且•=﹣2,则与的夹角为( ) A.150° B.120° C.60° D.30° 13 【考点】9R:平面向量数量积的运算. 【分析】运用向量的夹角公式:cos<,>=,再由夹角的范围即可得到. 【解答】解:由于||=1,||=4且•=﹣2, 则cos<,>===﹣, 由于0°≤<,>≤180°, 则与的夹角为120°. 故选B. 【点评】本题考查平面向量的数量积的定义和性质,考查向量的夹角的求法,属于基础题. 10.某商场出售三种品牌电脑,现存分别是60台、36台和24台,用分层抽样的方法从中抽取10台进行检测,这三种品牌的电脑依次应抽取的台数是( ) A.6,3,1 B.5,3,2 C.5,4,1 D.4,3,3 【考点】B3:分层抽样方法. 【分析】根据分层抽样原理,计算这三种品牌的电脑依次应抽取的台数即可. 【解答】解:根据分层抽样原理,从中抽取10台时, 这三种品牌的电脑依次应抽取的台数是 10×=5, 10×=3, 10×=2. 故选:B. 【点评】本题考查了分层抽样原理的应用问题,是基础题. 11.已知函数f(x)=,则f[f(2)]的值为( ) A.﹣1 B.1 C.4 D.5 13 【考点】3T:函数的值. 【分析】由函数的性质得f(2)=2+1=3,从而f[f(2)]=f(3),由此能求出结果. 【解答】解:∵函数f(x)=, ∴f(2)=2+1=3, f[f(2)]=f(3)=4. 故选:C. 【点评】本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用. 12.下列函数是偶函数的是( ) A.y=x B.y=2x2﹣3 C. D.y=x2,x∈[0,1] 【考点】3J:偶函数. 【分析】根据偶函数的定义“对于函数f(x)的定义域内任意一个x,都满足f(x)=f(﹣x),则函数f(x)为偶函数”进行判定. 【解答】解:对于A,f(﹣x)=﹣x=﹣f(x),是奇函数 对于B,定义域为R,满足f(x)=f(﹣x),是偶函数 对于C,定义域为[0,+∞)不对称,则不是偶函数; 对于D,定义域为[0,1]不对称,则不是偶函数 故选B. 【点评】本题主要考查了偶函数的定义,同时考查了解决问题、分析问题的能力,属于基础题. 13.下列四个图形是两个变x,y的散点图,其中具有线性相关关系的是( ) A. B. C. D. 【考点】BI:散点图. 【分析】散点图中所有点都在一条直线附近波动,是线性相关,否则不是. 【解答】解:根据两个变量之间的散点图知, 13 A中所有点都在一条直线附近波动,是线性相关; B、C、D中所有点都不在某条直线附近波动,是非线性相关. 故选:A. 【点评】本题考查了由散点图反应两个变量的相关关系问题,是基础题. 14.设a=(),b=(),c=(),则a,b,c的大小关系是( ) A.a>c>b B.a>b>c C.c>a>b D.b>c>a 【考点】4W:幂函数图象及其与指数的关系. 【分析】根据幂函数与指数函数的单调性直接可以判断出来. 【解答】解:∵在x>0时是增函数 ∴a>c 又∵在x>0时是减函数,所以c>b 故答案选A 【点评】本题主要考查幂函数与指数的关系.要充分利用函数图象、函数的单调性来解决问题. 二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上. 15.已知集合A={x|x>1},B={x|x2﹣2x﹣3<0},则A∩B= (1,3) . 【考点】1E:交集及其运算. 【分析】求出B中不等式的解集,找出A与B的交集即可. 【解答】解:由B中不等式变形得:(x﹣3)(x+1)<0, 解得:﹣1<x<3,即B=(﹣1,3), ∵A=(1,+∞), 则A∩B=(1,3), 故答案为:(1,3) 【点评】此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键. 16.sinα=3cosα,则tanα= 3 . 【考点】GG:同角三角函数间的基本关系. 13 【分析】已知等式两边除以cosα,利用同角三角函数间基本关系化简求出tanα的值即可. 【解答】解:∵sinα=3cosα, ∴=3, 则tanα=3, 故答案为:3 【点评】此题考查了同角三角函数间的基本关系,熟练掌握基本关系是解本题的关键. 17.已知向量=(﹣1,3),=(﹣3,x),若∥,则x= 9 ;若,则x= ﹣1 . 【考点】9R:平面向量数量积的运算;9K:平面向量共线(平行)的坐标表示. 【分析】直接利用向量的平行的充要条件与垂直的充要条件计算求解即可. 【解答】解:向量=(﹣1,3),=(﹣3,x),若∥, ﹣3×3=﹣x 则x=9. 若, 3+3x=0 则x=﹣1 故答案为:9;﹣1. 【点评】本题考查向量的数量积与向量的平行与垂直条件的应用,考查计算能力. 18.函数f(x)=的定义域是 {x|x>2且x≠3} . 【考点】33:函数的定义域及其求法;4K:对数函数的定义域. 【分析】根据对数函数及分式有意义的条件可得,解不等式可得 【解答】解:根据对数函数及分式有意义的条件可得 13 解可得,x>2且x≠3 故答案为:{x|x>2且x≠3} 【点评】本题属于以函数的定义为平台,求集合的交集的基础题,也是高考常考的基础型. 三、解答题共4小题,共42分.解答应写出文字说明,演算步骤或证明过程. 19.(10分)(2017春•河北期中)等差数列 {an}中,已知a2=3,a7=13 (1)求数列 {an}的通项公式; (2)求数列 {an}前10项的和S10. 【考点】85:等差数列的前n项和. 【分析】(1)利用等差数列的通项公式即可得出. (2)利用等差数列的求和公式即可得出. 【解答】解:(1)设等差数列 {an}的公差为d,∵a2=3,a7=13, ∴a1+d=3,a1+6d=13, 联立解得a1=1,d=2. ∴an=1+2(n﹣1)=2n﹣1. (2)S10=10×1+=100. 【点评】本题考查了等差数列的通项公式及其求和公式,考查了推理能力与计算能力,属于中档题. 20.(10分)(2016•沙河市校级学业考试)求圆心C在直线y=2x上,且经过原点及点M(3,1)的圆C的方程. 【考点】J1:圆的标准方程. 【分析】设出圆的圆心坐标,利用圆的半径相等,求出圆心坐标,即可得到圆的方程. 13 【解答】解:由题意设圆的圆心(a,2a), 则|OC|=|OM|,即:a2+(2a)2=(a﹣3)2+(2a﹣1)2,解得a=1, 所以圆心坐标(1,2),半径为:. 圆C的方程:(x﹣1)2+(y﹣2)2=5 【点评】本题考查圆的标准方程的求法,准确利用已知条件列出方程是解题的关键. 21.(10分)(2017春•河北期中)如图,点P为矩形ABCD所在平面外一点,PA⊥平面ABCD,点E为PA的中点. 求证:PC∥平面BED. 【考点】LS:直线与平面平行的判定. 【分析】连结AC、BD,交于点O,连结OE推导出OE∥PC,由此能证明PC∥平面BED. 【解答】证明:连结AC、BD,交于点O,连结OE, ∵点P为矩形ABCD所在平面外一点,∴O是AC中点, ∵点E为PA的中点,∴OE∥PC, ∵PC⊄平面BED,OE⊂平面BED, ∴PC∥平面BED. 【点评】本题考查线面平行的证明,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题. 13 22.(12分)(2017春•河北期中)已知sinθ=﹣.其中θ是第三象限角. (Ⅰ)求cosθ,tanθ的值; (Ⅱ)求的值. 【考点】GH:同角三角函数基本关系的运用. 【分析】(Ⅰ)由题意,利用同角三角函数的基本关系求得cosθ,tanθ的值. (Ⅱ)利用两角差的正切公式求得的值. 【解答】解:∵sinθ=﹣,其中θ是第三象限角, (Ⅰ)∴cosθ=﹣=﹣,tanθ==2. (Ⅱ)===﹣1. 【点评】题主要考查同角三角函数的基本关系,两角差的正切公式的应用,属于基础题. 13查看更多