2019-2020学年江西省上饶中学高二上学期期中考试（零培班）数学（文） Word版

2019-2020学年江西省上饶中学高二上学期期中考试（零培班）数学（文） Word版

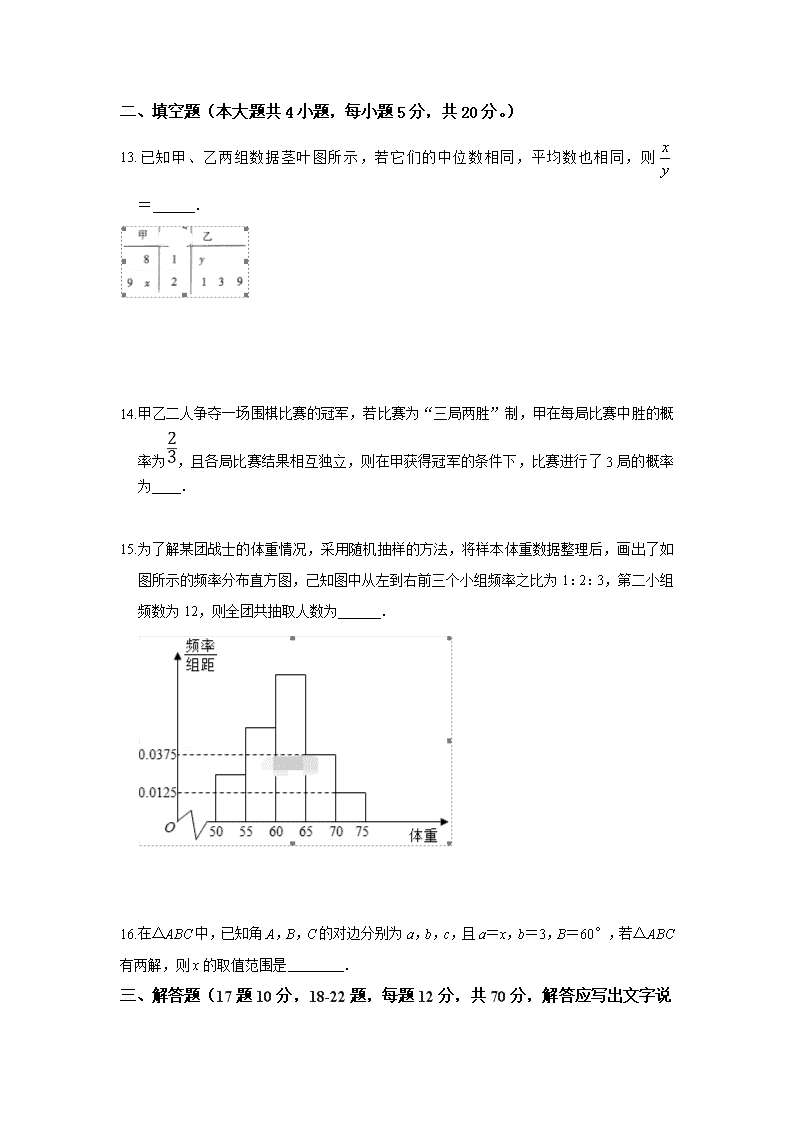
上饶中学2019-2020学年高二上学期期中考试 数学试卷（文科零培班）‎ 命题人：郑金秀 考试时间: 120分钟 分值：150分 一、 选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1.若M＝2a2﹣3a+5，N＝a2﹣a+4，则M与N的大小关系为（　　）‎ A．M≥N B．M＞N C．M＜N D．M≤N ‎2.某地甲、乙、丙三所学校举行高三联考，三所学校参加联考的人数分别为300，400，500，现为了调查联考数学学科的成绩，采用分层抽样的方法在这三所学校中抽取一个容量为120的样本，那么在乙学校中抽取的数学成绩的份数为（　　）‎ A．30 B．40 C．50 D．80‎ ‎3.若实数x，y满足，则z＝y﹣2x的最小值为（　 ）‎ A．2 B．﹣2 C．1 D．﹣1‎ ‎4.等差数列{an}中，a1＝1，a3﹣a2＝2，下列结论错误的是（　）‎ A．a1，a2，a5成等比数列 B．S9＝81 ‎ C．a7＝14 D．a4＝7‎ ‎5.不等式的解集为（　）‎ A．（﹣∞，﹣1]∪[2，+∞） B． ‎ C． D．‎ ‎6．已知△ABC的三个内角A，B，C所对边长分别为a，b，c，满足（a+c）（a﹣c）＝b（a﹣b），则∠C＝（　）‎ A． B． C． D．‎ ‎7.已知总体的各个体的值由小到大依次为2，3，3，7，x，y，12，13.6，18.4，20，且总体的中位数为10.5．若要使该总体的标准差最小，则4x+2y的值是（　）‎ A．61 B．62 C．63 D．64‎ ‎8.如图所示的算法被称为“趋1数字器”，它输出的数字都是分数，且随着运算次数的增加，输出的分数会越来越接近于1．该程序若想输出的结果为，则判断框中应填入的条件是（　）‎ A.i＜2011？ B．i＜2010？‎ C．i＜2009？ D．i＜2008？‎ ‎9.若不等式ax2+ax﹣1≤0的解集为实数集R，则实数a的取值范围为（ ）‎ A．0≤a≤4 B．﹣4＜a＜0‎ C．﹣4≤a＜0 D．﹣4≤a≤0‎ ‎10.对于问题“已知关于x的不等式ax2+bx+c＞0的解集为（2，5），解关于x的不等式cx2+bx+a＞0”，给出如下一种解法：由ax2+bx+c＞0的解集为（2，5），得的解集为，即关于x的不等式cx2+bx+a＞0的解集为．类比上述解法，若关于x的不等式的解集为（1，3），则关于x的不等式的解集为（　 ）‎ A．（3，27） B．（3，9） C．（1，27） D．（1，9）‎ ‎11．在边长为2的正方形ABCD内任取一点P，使得∠APB的概率为（　　）‎ A．1 B． C． D．1‎ ‎12.在1和19之间插入n个数，使这n+2个数成等差数列，若这n个数中第一个为a，第n个为b，当取最小值时，n的值是（　 ）‎ A．4 B．5 C．6 D．7‎ 二、填空题（本大题共4小题，每小题5分，共20分。）‎ 13. 已知甲、乙两组数据茎叶图所示，若它们的中位数相同，平均数也相同，则＝　 　．‎ ‎14.甲乙二人争夺一场围棋比赛的冠军，若比赛为“三局两胜”制，甲在每局比赛中胜的概率为，且各局比赛结果相互独立，则在甲获得冠军的条件下，比赛进行了3局的概率为　　．‎ ‎15.为了解某团战士的体重情况，采用随机抽样的方法，将样本体重数据整理后，画出了如图所示的频率分布直方图，己知图中从左到右前三个小组频率之比为1：2：3，第二小组频数为12，则全团共抽取人数为　 　．‎ ‎16.在△ABC中，已知角A，B，C的对边分别为a，b，c，且a＝x，b＝3，B＝60°，若△ABC有两解，则x的取值范围是　 　．‎ 三、解答题（17题10分，18-22题，每题12分，共70分，‎ 解答应写出文字说明，证明过程或演算步骤）‎ ‎17.根据教育部高考改革指导意见，广东省从2021年正式实施“3+1+2”新的高考考试方案．为尽快了解学生的选科需求，及时调整学校人力资源配备．某校从高一学生中抽样调查了100名同学，在模拟分科选择中，一半同学（其中男生38人）选择了物理，另一半（其中男生14人）选择了历史．请完成以下2×2列联表，并判断能否有99.9%的把握说选科与性别有关？‎ 参考公式：，其中n＝a+b+c+d为样本容量．‎ p（K2≥k）‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ k ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ 选物理 选历史 总计 男生 女生 总计 ‎18.甲与乙午觉醒来后，发现自己的手表因故停止转动，于是他们想借助收音机，利用电台整点报时确认时间．‎ ‎（1）求甲等待的时间不多于10分钟的概率；‎ ‎（2）求甲比乙多等待10分钟以上的概率．‎ ‎19.在△ABC中，角A，B，C所对的边分别为a，b，c，sinB+cosB＝1．‎ ‎（1）求角B；‎ ‎（2）若b，求△ABC周长的取值范围．‎ ‎20.已知不等式ax2﹣3x+6＞4的解集为{x|x＜1或x＞b}，‎ ‎（1）求a，b；‎ ‎（2）解不等式ax2﹣（ac+b）x+bc＜0‎ ‎21.某企业为确定下一年投入某种产品的研发费用，需了解年研发费用x（单位：千万元）对年销售量y（单位：千万件）的影响，统计了近10年投入的年研发费用xi与年销售量yi（i＝1，2…，10）的数据，得到散点图如图所示．‎ ‎（1）利用散点图判断y＝a+bx和y＝c•xd（其中c，d均为大于0的常数）哪一个更适合作为年销售量y和年研发费用x的回归方程类型（只要给出判断即可，不必说明理由）；‎ ‎（2）对数据作出如下处理，令ui＝lnxi，vi＝lnyi，得到相关统计量的值如表：根据第（1）问的判断结果及表中数据，求y关于x的回归方程；‎ vi ui ‎（ui）（vi）‎ ‎（ui）2‎ ‎15‎ ‎15‎ ‎28.25‎ ‎56.5‎ 附：对于一组数据（u1，v1），（u2，v2），…，（un，vn），其回归直线＝+的斜率和截距的最小二乘估计分别为＝，＝．‎ ‎22.已知数列{an}的前n项和为Sn，且Sn＝2an﹣n（n∈N*）．‎ ‎（1）证明数列{an+1}是等比数列，并求数列{an}的通项公式；‎ ‎（2）记bn＝（2n﹣1）an，求数列{bn}的前n项和Tn．‎