2021届课标版高考理科数学大一轮复习课件：8-4　直线、平面垂直的判定与性质（讲解部分）

2021届课标版高考理科数学大一轮复习课件：8-4　直线、平面垂直的判定与性质（讲解部分）

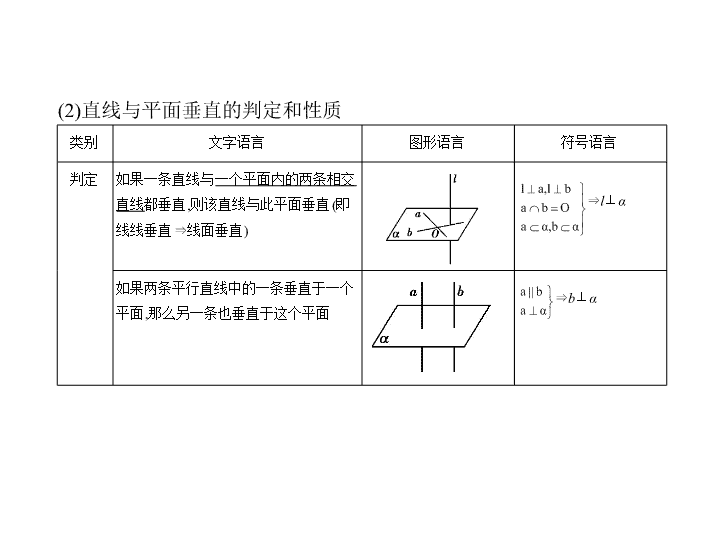
8.4 　直线、平面垂直的判定与性质 高考理数 考点一    直线与平面垂直的判定与性质 考点清单 考向基础 1.直线与平面垂直 (1)直线与平面垂直的定义 如果直线 l 和平面 α 内的 任意一条 直线都垂直,我们就说直线 l 与平面 α 垂直, 记作 l ⊥ α . 类别 文字语言 图形语言 符号语言 判定 如果一条直线与 一个平面内的两条相交直线 都垂直,则该直线与此平面垂直(即线线垂直 ⇒ 线面垂直)     ⇒ l ⊥ α 如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于这个平面     ⇒ b ⊥ α (2)直线与平面垂直的判定和性质 性质 如果一条直线和一个平面垂直,则这条直线垂直于平面内任意一条直线 (即线面垂直 ⇒ 线线垂直)     ⇒ a ⊥ b 垂直于同一个平面的两条直线平行     ⇒ a ∥ b 2.直线与平面所成的角 (1)定义:平面的一条斜线和它在平面上的射影所成的 锐角 叫做这条直线和 这个平面所成的角.一条直线垂直于平面,我们说它们所成的角是直角;一 条直线和平面平行,或在平面内,我们说它们所成的角是0 ° 的角. (2)最小角定理:平面的斜线和它在平面内的射影所成的角是这条斜线和这 个平面内任一条直线所成角中最小的角. (3) 线面角 θ 的取值范围:0 ° ≤ θ ≤ 90 ° . 常用结论　(1) 过一点有且只有一条直线与已知平面垂直. (2) 过一点有且只有一个平面与已知直线垂直. 考向突破 考向一    证明空间直线与平面垂直 例1　 在如图所示的直三棱柱 ABC - A 1 B 1 C 1 中, AC =1, BC =   , AB =   ,侧棱 AA 1 =1,点 D , M 分别为 A 1 B , B 1 C 1 的中点. (1)求证: CD ⊥平面 A 1 BM ; (2)求三棱锥 M - A 1 BC 的体积.   解析 　(1)证明:∵ AC =1, BC =   , AB =   ,满足 AC 2 + BC 2 = AB 2 , ∴ AC ⊥ BC . ∵三棱柱 ABC - A 1 B 1 C 1 为直三棱柱, ∴ CC 1 ⊥ BC , 又∵ AC ∩ CC 1 = C ,∴ BC ⊥平面 ACC 1 A 1 . ∵ A 1 C ⊂ 平面 ACC 1 A 1 ,∴ BC ⊥ A 1 C . ∵三棱柱 ABC - A 1 B 1 C 1 为直三棱柱, ∴ AA 1 ⊥ AC ,∴ A 1 C =   , 又∵ BC =   , D 为 A 1 B 的中点, ∴ CD ⊥ A 1 B ,且 CD =     =1. 连接 MD ,如图. 易求 A 1 M = BM = CM =   , 又∵点 D 为 A 1 B 的中点, ∴ MD ⊥ A 1 B ,且 MD =   =   . 又 CM =   ,∴ CM 2 = CD 2 + MD 2 ,∴ CD ⊥ MD . 又 A 1 B ⊂ 平面 A 1 BM , MD ⊂ 平面 A 1 BM , A 1 B ∩ MD = D , ∴ CD ⊥平面 A 1 BM . (2)由(1)知 CD ⊥平面 A 1 BM , ∵ A 1 B =   =2, MD =   , A 1 B ⊥ MD , ∴   =   =   ·   · CD =   ×   × 1=   . 考向二    证明空间两直线垂直 例2     (2019河南安阳3月检测,18)如图,在四棱锥 P - ABCD 中, PA ⊥底面 ABCD , AB ⊥ AD , AC ⊥ CD ,∠ ABC =60 ° , PA = AB = BC , E 是 PC 的中点.求证: (1) CD ⊥ AE ; (2) PD ⊥平面 ABE .   证明 　(1)因为 PA ⊥平面 ABCD , CD ⊂ 平面 ABCD , 所以 PA ⊥ CD . 因为 AC ⊥ CD , PA ∩ AC = A , 所以 CD ⊥平面 PAC . 又 AE ⊂ 平面 PAC ,所以 CD ⊥ AE . (2)由 PA = AB = BC ,∠ ABC =60 ° ,可得 AC = PA . 因为 E 是 PC 的中点,所以 AE ⊥ PC . 由(1)知, AE ⊥ CD ,且 PC ∩ CD = C , 所以 AE ⊥平面 PCD . 又 PD ⊂ 平面 PCD ,所以 AE ⊥ PD . 因为 PA ⊥平面 ABCD , AB ⊂ 平面 ABCD , 所以 PA ⊥ AB . 又 AB ⊥ AD , PA ∩ AD = A , 所以 AB ⊥平面 PAD , 又 PD ⊂ 平面 PAD ,所以 AB ⊥ PD . 又 AE ∩ AB = A ,所以 PD ⊥平面 ABE . 考点二    平面与平面垂直的判定与性质 考向基础 1.二面角的平面角 从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二 面角的棱,这两个半平面叫做二面角的面.如果记棱为 l ,那么两个面分别为 α 、 β 的二面角记作 α - l - β . 在二面角的棱上任取一点,以该点为垂足,在两个半平面内分别作垂直于棱 的射线,则两射线所构成的角叫做二面角的平面角. 类别 文字语言 图形语言 符号语言 判定 两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直   ∠ AOB 是二面角 α - l - β 的 平面角,且∠ AOB =90 ° , 则 α ⊥ β 如果一个平面过另一个平面的垂线,则这两个平面互相垂直(即线面垂直 ⇒ 面面垂直)     ⇒ β ⊥ α 2.面面垂直的判定和性质 性质 如果两个平面垂直,则其中一个平面内垂直于交线的直线垂直于另一个平面     ⇒ l ⊥ α 如果两个相交平面同时垂直于第三个平面,那么它们的交线垂直于第三个平面     ⇒ l ⊥ γ 【知识拓展】    垂直问题的转化方向图   在垂直关系中,线面垂直是核心,已知线面垂直,既可为证明线线垂直提供 依据,又可为利用判定定理证明面面垂直做好铺垫.应用面面垂直的性质定 理时,一般需作辅助线,基本作法是过其中一个平面内一点作交线的垂线, 从而把面面垂直问题转化为线面垂直问题,进而可转化为线线垂直问题. 考向突破 考向一    证明平面与平面垂直 例1     (2018安徽淮北一中模拟,18)如图,四棱锥 P - ABCD 的底面是矩形, PA ⊥平面 ABCD , E , F 分别是 AB , PD 的中点,且 PA = AD .   (1)求证: AF ∥平面 PEC ; (2)求证:平面 PEC ⊥平面 PCD . 证明 　(1)取 PC 的中点 G ,连接 FG 、 EG ,   ∵ F 为 PD 的中点, G 为 PC 的中点, ∴ FG 为△ CDP 的中位线,∴ FG ∥ CD , FG =   CD . ∵四边形 ABCD 为矩形, E 为 AB 的中点, ∴ AE ∥ CD , AE =   CD . ∴ FG = AE , FG ∥ AE ,∴四边形 AEGF 是平行四边形, ∴ AF ∥ EG ,又 EG ⊂ 平面 PEC , AF ⊄ 平面 PEC , ∴ AF ∥平面 PEC . (2)∵ PA = AD , F 为 PD 的中点,∴ AF ⊥ PD , ∵ PA ⊥平面 ABCD , CD ⊂ 平面 ABCD ,∴ PA ⊥ CD , 又∵ CD ⊥ AD , AD ∩ PA = A ,∴ CD ⊥平面 PAD , ∵ AF ⊂ 平面 PAD ,∴ CD ⊥ AF , 又 PD ∩ CD = D ,∴ AF ⊥平面 PCD , 由(1)知 EG ∥ AF ,∴ EG ⊥平面 PCD , 又 EG ⊂ 平面 PEC , ∴平面 PEC ⊥平面 PCD . 考向二    垂直关系中的存在性问题 例2     如图所示,在四棱锥 P - ABCD 中,底面 ABCD 是∠ DAB =60 ° 且边长为 a 的菱形,侧面 PAD 为正三角形,其所在平面垂直于底面 ABCD ,若 G 为 AD 的中点.   (1)求证: BG ⊥平面 PAD ; (2)求证: AD ⊥ PB ; (3)若 E 为 BC 边的中点,能否在棱 PC 上找到一点 F ,使平面 DEF ⊥平面 ABCD ? 并证明你的结论. 解析 　(1)证明:在菱形 ABCD 中,∠ DAB =60 ° , G 为 AD 的中点,所以 BG ⊥ AD . 又平面 PAD ⊥平面 ABCD ,平面 PAD ∩ 平面 ABCD = AD , 所以 BG ⊥平面 PAD . (2)证明:如图,连接 PG ,因为△ PAD 为正三角形, G 为 AD 的中点,所以 PG ⊥ AD .   由(1)知 BG ⊥ AD ,又 PG ∩ BG = G ,所以 AD ⊥平面 PGB . 因为 PB ⊂ 平面 PGB ,所以 AD ⊥ PB . (3)当 F 为 PC 的中点时,满足平面 DEF ⊥平面 ABCD . 证明:取 PC 的中点 F ,连接 DE 、 EF 、 DF . 在△ PBC 中, FE ∥ PB ,在菱形 ABCD 中, GB ∥ DE . 又 FE ⊂ 平面 DEF , DE ⊂ 平面 DEF , EF ∩ DE = E , PB ⊂ 平面 PGB , GB ⊂ 平面 PGB , PB ∩ GB = B , 所以平面 DEF ∥平面 PGB . 因为 BG ⊥平面 PAD , PG ⊂ 平面 PAD , 所以 BG ⊥ PG . 又因为 PG ⊥ AD , AD ∩ BG = G , 所以 PG ⊥平面 ABCD . 又 PG ⊂ 平面 PGB ,所以平面 PGB ⊥平面 ABCD , 所以平面 DEF ⊥平面 ABCD . 方法1      证明直线与平面垂直的方法 (1)利用线面垂直的判定定理: a ⊥ b , a ⊥ c , b ∩ c = M , b ⊂ α , c ⊂ α ⇒ a ⊥ α . (2)利用平行线垂直平面的传递性: a ∥ b , a ⊥ α ⇒ b ⊥ α . (3)利用面面垂直的性质定理: α ⊥ β , α ∩ β = l , a ⊥ l , a ⊂ β ⇒ a ⊥ α . (4)利用面面平行的性质: α ∥ β , a ⊥ β ⇒ a ⊥ α . (5)利用面面垂直的性质: α ∩ β = l , α ⊥ γ , β ⊥ γ ⇒ l ⊥ γ . 方法技巧 例1      S 是Rt△ ABC 所在平面外一点,且 SA = SB = SC , D 为斜边 AC 的中点. (1)求证: SD ⊥平面 ABC ; (2)若 AB = BC ,求证: BD ⊥平面 SAC . 解题导引   证明　 (1)如图所示,取 AB 的中点 E ,连接 SE , DE , 在Rt△ ABC 中, D 、 E 分别为 AC 、 AB 的中点, ∴ DE ∥ BC ,∴ DE ⊥ AB . ∵ SA = SB ,∴△ SAB 为等腰三角形, ∴ SE ⊥ AB . 又 SE ∩ DE = E ,∴ AB ⊥平面 SDE . 又 SD ⊂ 平面 SDE ,∴ AB ⊥ SD . 在△ SAC 中, SA = SC , D 为 AC 的中点,∴ SD ⊥ AC . 又 AC ∩ AB = A ,∴ SD ⊥平面 ABC . (2)由于 AB = BC ,则 BD ⊥ AC , 由(1)可知, SD ⊥平面 ABC , 又 BD ⊂ 平面 ABC ,∴ SD ⊥ BD , 又 SD ∩ AC = D ,∴ BD ⊥平面 SAC . 方法2      证明平面与平面垂直的方法 1.利用面面垂直的定义(作出两平面构成的二面角的平面角,计算平面角为 90 ° ); 2.利用面面垂直的判定定理: a ⊥ β , a ⊂ α ⇒ α ⊥ β . 利用面面垂直的判定定理证明面面垂直的一般方法:先从现有的直线中寻 找平面的垂线,若这样的直线在图中存在,则可通过线面垂直来证明面面垂 直;若这样的直线在图中不存在,则可通过作辅助线来解决.作辅助线应有 理论根据并有利于证明,不能随意添加. 证明两个平面垂直,通常是通过证明 线线垂直→线面垂直→面面垂直 来实 现的,因此,在关于垂直问题的论证中要注意线线垂直、线面垂直、面面垂 直的相互转化. 例2     (2018河南洛阳一模,19)如图,在四棱锥 E - ABCD 中,△ EAD 为等边三角 形,底面 ABCD 为等腰梯形,满足 AB ∥ CD , AD = DC =   AB ,且 AE ⊥ BD . (1)证明:平面 EBD ⊥平面 EAD ; (2)若△ EAD 的面积为   ,求点 C 到平面 EBD 的距离.   解题导引   解析 　(1)证明:如图,取 AB 的中点 M ,连接 DM ,由题意可知四边形 BCDM 为平 行四边形,∴ DM = CB = AD =   AB ,   (1分) 即点 D 在以线段 AB 为直径的圆上, ∴ BD ⊥ AD ,   (3分) 又 AE ⊥ BD ,且 AE ∩ AD = A , ∴ BD ⊥平面 EAD .   (4分) ∵ BD ⊂ 平面 EBD ,∴平面 EBD ⊥平面 EAD .   (6分)   (2)∵ BD ⊥平面 EAD ,且 BD ⊂ 平面 ABCD , ∴平面 ABCD ⊥平面 EAD .   (7分) ∵等边△ EAD 的面积为   , ∴ AD = AE = ED =2.   (8分) 取 AD 的中点 O ,连接 EO ,则 EO ⊥ AD , EO =   , ∵平面 EAD ⊥平面 ABCD ,平面 EAD ∩ 平面 ABCD = AD ,∴ EO ⊥平面 ABCD . 由(1)知△ ABD ,△ EBD 都是直角三角形, ∴ BD =   =2   ,∴ S △ EBD =   ED · BD =2   .   (10分) 设点 C 到平面 EBD 的距离为 h ,由 V C - EBD = V E - BCD ,得   S △ EBD · h =   S △ BCD · EO , 又 S △ BCD =   BC · CD sin 120 ° =   , ∴ h =   .∴点 C 到平面 EBD 的距离为   .   (12分)