河北省邯郸市大名县第一中学2019-2020学年高二下学期3月月考数学试题
高二3月份考试数学试题
命题人:张晓艳 审题人:郭冰
一、选择题(本大题共12小题,每题5分,共60分)
1.设复数z满足(1+i)z=2i,则|z|=( )
A. B.
C. D. 2
【答案】C
【解析】
【分析】
先求出表达式,然后对其化简,求出复数的模即可.
【详解】由题意,,所以.
故选:C.
【点睛】本题考查复数的四则运算,考查复数的模的计算,属于基础题.
2.已知,,则是的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
【答案】A
【解析】
【分析】
根据题意解不等式可得集合p与q的范围,根据充分必要条件的判定即可判断结论.
【详解】因为
所以,
所以但
所以是的充分不必要条件
所以选A
【点睛】本题考查了根据不等式判定充分必要条件,属于基础题.
3.教学大楼共有四层,每层都有东西两个楼梯,从一层到四层共有( )种走法
A. B. C. D.
【答案】B
【解析】
【分析】
根据题意,分析层与层之间的走法数目,利用分步计数原理计算可得答案.
【详解】解:根据题意,教学大楼共有四层,每层都有东西两个楼梯,
则从一层到二层,有2种走法,同理从二层到三层、从三层到四层也各有2种走法,
则从一层到四层共有种走法.
故选:B.
【点睛】本题考查分步计数原理的应用,注意认真分析题意,注意四层的大楼有三层楼梯,属于基础题.
4. 6把椅子摆成一排,3人随机就座,任何两人不相邻的坐法种数为( )
A. 144 B. 120 C. 72 D. 24
【答案】D
【解析】
试题分析:先排三个空位,形成4个间隔,然后插入3个同学,故有种
考点:排列、组合及简单计数问题
5.安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有
A. 12种 B. 18种 C. 24种 D. 36种
【答案】D
【解析】
4项工作分成3组,可得:=6,
安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,
可得:种.
故选D.
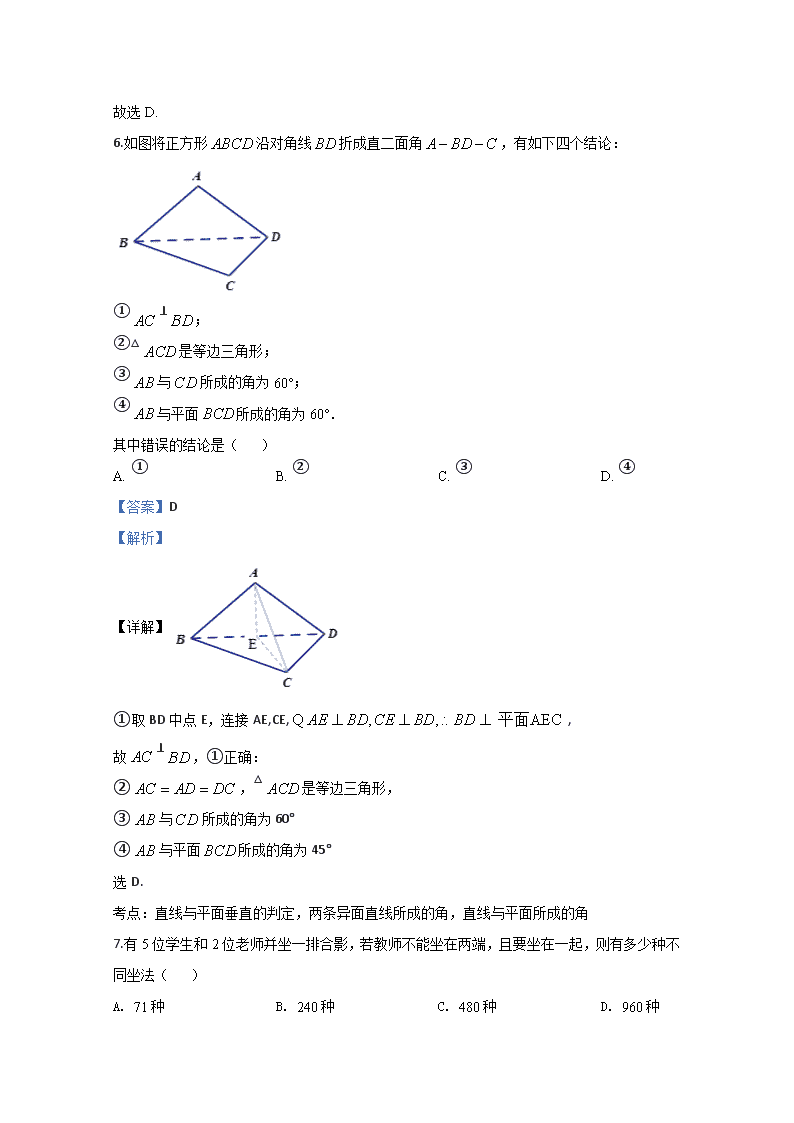
6.如图将正方形沿对角线折成直二面角,有如下四个结论:
①⊥;
②△是等边三角形;
③与所成的角为60°;
④与平面所成的角为60°.
其中错误的结论是( )
A. ① B. ② C. ③ D. ④
【答案】D
【解析】
【详解】
①取BD中点E,连接AE,CE,,
故⊥,①正确:
②,△是等边三角形,
③与所成的角为60°
④与平面所成的角为45°
选D.
考点:直线与平面垂直的判定,两条异面直线所成的角,直线与平面所成的角
7.有5位学生和2位老师并坐一排合影,若教师不能坐在两端,且要坐在一起,则有多少种不同坐法( )
A. 71种 B. 240种 C. 480种 D. 960种
【答案】D
【解析】
【分析】
先排5位学生,由排列公式可得其坐法数目,要求2位教师坐在一起,用捆绑法,插入到5个学生符合要求的4个空位中,易得其有种坐法,由分步计数原理计算可得答案.
【详解】解:先排5位学生,有种坐法,
2位教师坐在一起,将其看成一个整体,可以交换位置,有2种坐法,
将这个“整体”插在5个学生的空位中,又由教师不能坐在两端,则有4个空位可选,
则共有种坐法.
故选:D
【点睛】本题考查排列、组合的运用,关键在于掌握常见的问题的处理方法,如相邻问题用捆绑法,不相邻问题用插空法,属于基础题.
8.若函数在区间内恰有一个极值点,则实数的取值范围为( )
A. B. C. D.
【答案】B
【解析】
由题意,,
则,
即,
解得,
另外,当时,在区间(−1,1)恰有一个极值点,
当时,函数在区间(−1,1)没有一个极值点,
实数的取值范围为.
故选B.
9.
如图,花坛内有五个花池,有五种不同颜色的花卉可供栽种,每个花池内只能种同种颜色的花卉,相邻两池的花色不同,则最多有几种栽种方案( )
A. 180种 B. 240种 C. 360种 D. 420种
【答案】D
【解析】
【分析】
若5个花池栽了5种颜色的花卉,方法有种,若5个花池栽了4种颜色的花卉,方法有2种,若5个花池栽了3种颜色的花卉,方法有种,相加即得所求.
【详解】若5个花池栽了5种颜色的花卉,方法有种,
若5个花池栽了4种颜色的花卉,则2、4两个花池栽同一种颜色的花;
或者3、5两个花池栽同一种颜色的花,方法有2种,
若5个花池栽了3种颜色的花卉,方法有种,
故最多有+2+=420种栽种方案,
故选D.
【点睛】解答排列、组合问题的角度:解答排列、组合应用题要从“分析”、“分辨”、“分类”、“分步”的角度入手;(1)“分析”就是找出题目的条件、结论,哪些是“元素”,哪些是“位置”;(2)“分辨”就是辨别是排列还是组合,对某些元素的位置有、无限制等;(3)“分类”就是将较复杂的应用题中的元素分成互相排斥的几类,然后逐类解决;(4)“分步”就是把问题化成几个互相联系的步骤,而每一步都是简单的排列、组合问题,然后逐步解决.
10.设,是椭圆的左、右焦点,过的直线交椭圆于A,B两点,若最大值为5,则椭圆的离心率为( )
A. B. C. D.
【答案】A
【解析】
【分析】
,故的最小值为,当且仅当轴时,最小,此时,计算得到答案.
【详解】,
最大值为5,故最小值为,
当且仅当轴时,最小,此时,
即又因为,
可得,故.
故选:.
【点睛】本题考查了椭圆的离心率,意在考查学生的计算能力和转化能力.
11.在的展开式中的的系数为( )
A. 210 B. -210 C. -910 D. 280
【答案】C
【解析】
试题分析:,令,,或,代入得到系数:
考点:二项式定理的应用
12.定义在R上的函数的导函数为,若对任意实数x,有,且函数为奇函数,则不等式的解集是 ( )
A. B. C. D.
【答案】A
【解析】
设由f(x)>f′(x),
得:,
故函数g(x)在R递减,
由f(x)+2017为奇函数,得f(0)=−2017,
∴g(0)=−1,
∵f(x)+2017ex<0,∴,即g(x)
0,
故不等式f(x)+2017ex<0的解集是(0,+∞).
本题选择A选项.
点睛:函数的单调性是函数的重要性质之一,它的应用贯穿于整个高中数学的教学之中.某些数学问题从表面上看似乎与函数的单调性无关,但如果我们能挖掘其内在联系,抓住其本质,那么运用函数的单调性解题,能起到化难为易、化繁为简的作用.因此对函数的单调性进行全面、准确的认识,并掌握好使用的技巧和方法,这是非常必要的.根据题目的特点,构造一个适当的函数,利用它的单调性进行解题,是一种常用技巧.许多问题,如果运用这种思想去解决,往往能获得简洁明快的思路,有着非凡的功效.
二、填空题(本大题共4小题,每题5分,共20分)
13.命题:“”的否定为____.
【答案】
【解析】
【分析】
直接利用特称命题的否定是全称命题写出结果即可.
【详解】写命题否定时,除结论要否定外,存在量词与全称量词要互换,因此命题“”的否定是“”.
故答案为∀x∈R,x2﹣ax+1≥0
【点睛】本题考查命题的否定及特称命题与全称命题的关系,属于基本知识的考查.
14.7个人站成一排,若甲,乙,丙三人互不相邻的排法共有________种.
【答案】1440
【解析】
【分析】
因为要求不相邻,采用插空法来解,先排列另外四人,有种结果,再在排列好的四人的5个空里,排列甲、乙、丙,有种结果,根据分步计数原理相乘得到结果.
【详解】解:∵7个人站成一排,若甲、乙、丙彼此不相邻,
∴采用插空法来解,
先排列甲、乙、丙之外的4人,有种结果,
再在排列好的4人的5个空里,排列甲、乙、丙,有种结果,
根据分步计数原理知共有种结果,
故答案为:1440.
【点睛】本题考查排列组合及简单计数问题,在题目中要求元素不相邻,这种问题一般采用插空法,先排一种元素,再在前面元素形成的空里,排列不相邻的元素.属于基础题.
15.已知复数,,,且,则的最大值为________.
【答案】33
【解析】
【分析】
根据复数的几何意义计算可得;
【详解】解:复数,,,设,
由,表示复平面上点的轨迹是以为圆心,1为半径的圆.
则.
则与点的距离.
∴.
故答案为:33.
【点睛】本题主要考察了复数形式的圆的方程、两点之间的距离公式、点与圆的位置关系,考查了推理能力与计算能力,属于中档题.
16.从1,3,5,7,9中任取2个数字,从0,2,4,6中任取2个数字,一共可以组成___________个没有重复数字的四位数.(用数字作答)
【答案】1260.
【解析】
分析:按否取零分类讨论,若取零,则先排首位,最后根据分类与分步计数原理计数.
详解:若不取零,则排列数为若取零,则排列数为
因此一共有个没有重复数字的四位数.
点睛:求解排列、组合问题常用的解题方法:
(1)元素相邻的排列问题——“捆邦法”;(2)元素相间的排列问题——“插空法”;(3)元素有顺序限制的排列问题——“除序法”;(4)带有“含”与“不含”“至多”“至少”的排列组合问题——间接法.
三、解答题(本大题共6小题,共70分)
17.设,命题:,,命题:,满足.
(1)若命题是真命题,求的范围;
(2)为假,为真,求的取值范围.
【答案】(1).(2)或.
【解析】
【分析】
(1)根据、为真命题,列式计算.
(2)由为假,为真、同时为假或同时为真,分别求出实数的取值范围即可.
【详解】解:(1)真,则或得;
真,则,得
∵命题是真命题,
∴的范围为.
(2)由为假,为真,、同时为假或同时为真,
若假假,则,,
若真真,则,
综上或.
【点睛】本题主要考查复合命题与简单命题之间的关系的应用,利用条件先求出命题,的等价条件是解决本题的关键,属于中档题.
18.设,求:
(1);
(2);
(3);
(4).
【答案】(1)1;(2)243;(3)122;(4)
【解析】
【分析】
(1)令x=1即得;(2)在中,令得解;(3)
先求出f(1)-f(-1)即得解;(4)求f(1)·f(-1)即得解.
【详解】∵,
(1)令,可得;
(2)在中,令,可得;
(3)令f(x)=,
f(1)=,
所以f(-1)=,
所以f(1)-f(-1)=2,
所以.
(4)
.
【点睛】本题主要考查二项式展开式的系数的求法,意在考查学生对这些知识的理解掌握水平和分析推理能力.
19.已知抛物线的方程是,直线交抛物线于两点
(1)若弦AB的中点为,求弦AB的直线方程;
(2)设,若,求证AB过定点.
【答案】(1)y=x+1(2)见证明
【解析】
【分析】
(1)设出A,B坐标,结合弦AB的中点坐标,建立等式,计算直线AB的斜率,得到直线方程,即可.(2)设出AB的直线方程,代入抛物线方程,得到二次等式,结合根与系数的关系,得到AB的方程,计算定点,即可.
【详解】(1)因为抛物线的方程为,设,,
则有x1 ≠x2
,,
因为弦AB的中点为(3,3),
两式相减得,
所以,经验证符合题意.
所以直线l的方程为y-3=(x-3),即y=x+1 ;
(2)当AB斜率存在时,设AB方程为y=kx+b代入抛物线方程:
ky2-4y+4b=0,
,,
AB方程为y=kx-3k=k(x-3),恒过定点(3,0).
当AB斜率不存在时,,则x1=x2=3,过点(3,0).
综上,AB恒过定点(3,0).
【点睛】本道题考查了抛物线的基本性质,考查了直线与抛物线的位置关系,属于较难的题.
20.如图,在四棱锥中,棱、、两两垂直,且长度均为,.
(1)若,求直线与平面所成角的正弦值;
(2)若二面角的大小为,求实数的值.
【答案】(1)(2)
【解析】
【分析】
(1)以为原点,为轴,为轴,为
轴,建立空间直角坐标系,利用向量法能求出直线与平面所成角的正弦值;
(2)求出平面的一个法向量和平面的一个法向量,利用向量法能求出.
【详解】(1)以为原点,为轴,为轴,为轴,建立空间直角坐标系如图.
因为,所以.
依题意,,,,,
所以,,.
设平面的一个法向量为,
则,所以,取得.
所以.
所以,直线与平面所成角的正弦值为;
(2)依题意,,,,.
设平面的一个法向量为,
则即取得,.
设平面的一个法向量为,
则即取得,
所以,
解得或,因为,所以.
【点睛】本题考查利用空间向量法求解线面角、二面角,考查运算求解能力,是中档题.
21.已知,分别为椭圆:的左、右焦点,点在椭圆上.
(Ⅰ)求的最小值;
(Ⅱ)设直线的斜率为,直线与椭圆交于,两点,若点在第一象限,且,求面积的最大值.
【答案】(Ⅰ)的最小值为; (Ⅱ)2.
【解析】
【详解】试题分析:
(Ⅰ)设,由向量数量积的坐标运算求得,注意椭圆中有,因此可得最小值;
(Ⅱ)由直线与圆锥曲线相交的弦长公式求得弦长,求出点坐标,再求得到直线的距离即三角形的高,从而得面积由基本不等式可得最大值.
试题解析:
(Ⅰ)有题意可知,,
则,,
∴,
∵点在椭圆上,∴,即,
∴(),
∴当时,的最小值为.
(Ⅱ)设的方程,点,,
由得,
令,解得.
由韦达定理得,,
由弦长公式得,
由且,得.
又点到直线的距离,
∴ ,
当且仅当时,满足,等号成立,
∴面积最大值为2.
22.已知.
(1)讨论的单调性;
(2)当有最大值,且最大值大于时,求的取值范围.
【答案】(1) 在单调递增,在单调递减.
(2).
【解析】
试题分析:(Ⅰ)由,可分,两种情况来讨论;(II)由(I)知当
时在无最大值,当时最大值为因此.令,则在是增函数,当时,,当时,因此a的取值范围是.
试题解析:
(Ⅰ)的定义域为,,若,则,在是单调递增;若,则当时,当时,所以在单调递增,在单调递减.
(Ⅱ)由(Ⅰ)知当时在无最大值,当时在取得最大值,最大值为因此.令,则在是增函数,,于是,当时,,当时,因此a的取值范围是.
考点:本题主要考查导数在研究函数性质方面的应用及分类讨论思想.