高考数学复习专题模拟:第二章 函数与基本初等函数 第三节 函数、方程及其应用
【数学】2014版《6年高考4年模拟》
第三节 函数、方程及其应用
第一部分 六年高考荟萃
2013年高考题
.(2013年高考陕西卷(理))在如图所示的锐角三角形空地中, 欲建一个面积不小于300m2的内接矩形花园(阴影部分), 则其边长x(单位m)的取值范围是
(A) [15,20] (B) [12,25] (C) [10,30] (D) [20,30]
答案:C
【解析】设矩形高为y, 由三角形相似得: 利用线性规划知识解得,选C
.(2013年普通高等学校招生统一考试重庆数学(理)试题(含答案))的最大值为( )
A.9 B. C. D.
答案:B
本题考查函数的最值以及基本不等式的应用。当时,,当时,。所以,当且仅当,即时去等号。选B.
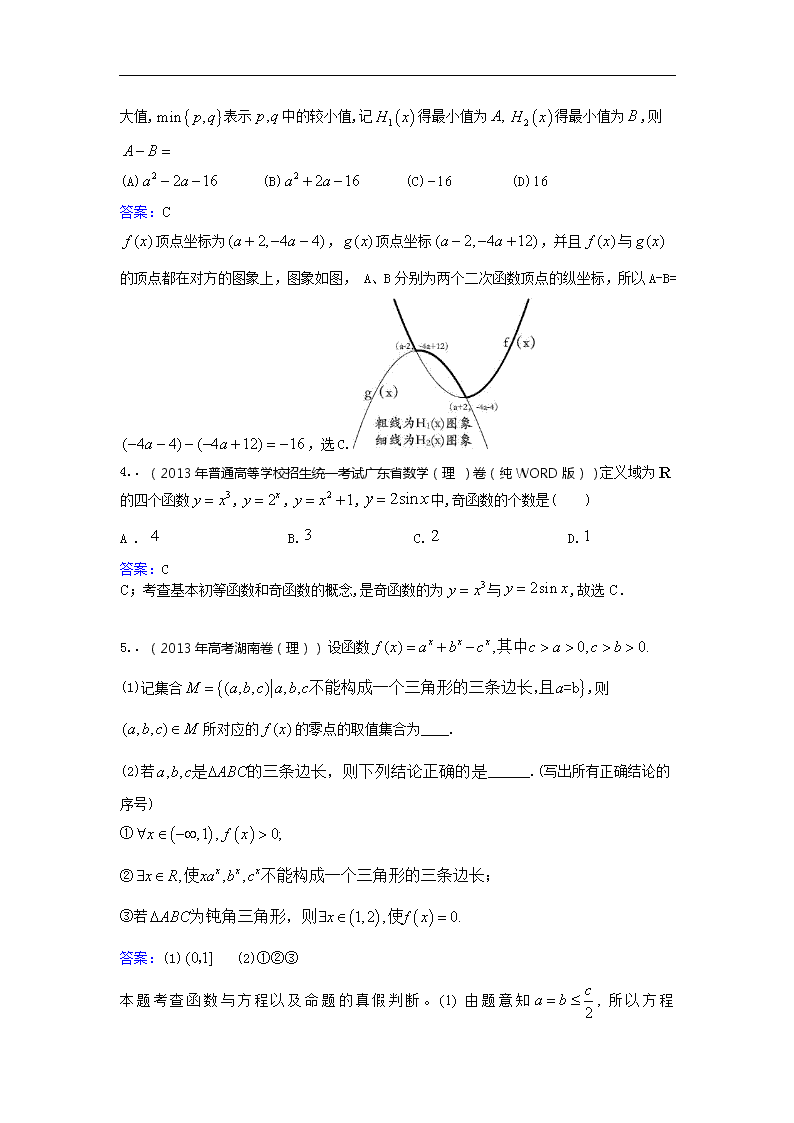
.(2013年普通高等学校招生统一考试辽宁数学(理)试题(WORD版))已知函数设表示中的较大值,表示中的较小值,记得最小值为得最小值为,则
(A) (B) (C) (D)
答案:C
顶点坐标为,顶点坐标,并且与的顶点都在对方的图象上,图象如图, A、B分别为两个二次函数顶点的纵坐标,所以A-B=,选C.
.(2013年普通高等学校招生统一考试广东省数学(理)卷(纯WORD版))定义域为的四个函数,,,中,奇函数的个数是( )
A . B. C. D.
答案:C
C;考查基本初等函数和奇函数的概念,是奇函数的为与,故选C.
.(2013年高考湖南卷(理))设函数
(1)记集合,则所对应的的零点的取值集合为____.
(2)若______.(写出所有正确结论的序号)
①
②
③若
答案:(1) (2)①②③
本题考查函数与方程以及命题的真假判断。(1)由题意知,所以方程可化为,即又,所以当时
此时;当时,无解.所以的零点的取值集合为.
(2) ①令,
则,因为所以,
即,所以是单调递减函数,所以在上,
又,
所以
②又因为是单调递减函数,所以在一定存在零点,即,此时不能构成三角形的三边.
③由余弦定理易知,即,又,且连续,所以故①②③都正确。
2012年高考题
1.[2012·北京卷] 某棵果树前n年的总产量Sn与n之间的关系如图1-6所示.从目前记录的结果看,前m年的年平均产量最高,m值为( )
图1-6
A.5 B.7 C.9 D.11
答案:C [解析] 本题考查利用函数图像识别函数值的变化趋势,也就是函数增减速度的快慢.
法一:因为随着n的增大,Sn在增大,要使取得最大值,只要让随着n的增大Sn+1-Sn
的值超过(平均变化)的加入即可,Sn+1-Sn的值不超过(平均变化)的舍去,由图像可知,6,7,8,9这几年的改变量较大,所以应该加入,到第10,11年的时候,改变量明显变小,所以不应该加入,故答案为C.
法二:假设是取的最大值,所以只要>即可,也就是>,即可以看作点Qm(m,Sm)与O(0,0)连线的斜率大于点Qm+1(m+1,Sm+1)与O(0,0)连线的斜率,所以观察可知到第Q9(9,S9)与O(0,0)连线的斜率开始大于点Q10(10,S10)与O(0,0)连线的斜率.答案为C.
2.[2012·上海卷] 海事救援船对一艘失事船进行定位:以失事船的当前位置为原点,以正北方向为y轴正方向建立平面直角坐标系(以1海里为单位长度),则救援船恰好在失事船正南方向12海里A处,如图1-4.现假设:①失事船的移动路径可视为抛物线y=x2;②定位后救援船即刻沿直线匀速前往救援;③救援船出发t小时后,失事船所在位置的横坐标为7t.
(1)当t=0.5时,写出失事船所在位置P的纵坐标.若此时两船恰好会合,求救援船速度的大小和方向;(2)问救援船的时速至少是多少海里才能追上失事船?
解:(1)t=0.5时,P的横坐标xP=7t=,代入抛物线方程y=x2,得P的纵坐标yP=3.
由|AP|=,得救援船速度的大小为海里/时.
由tan∠OAP=,得∠OAP=arctan,故救援船速度的方向为北偏东arctan弧度.
(2)设救援船的时速为v海里,经过t小时追上失事船,此时位置为(7t,12t2).
由vt=,
整理得v2=144+337.
因为t2+≥2,当且仅当t=1时等号成立.
所以v2≥144×2+337=252,即v≥25.
因此,救援船的时速至少是25海里才能追上失事船.
3.[2012·北京卷] 已知函数f(x)=ax2+1(a>0),g(x)=x3+bx.
(1)若曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处具有公共切线,求a,b的值;
(2)当a2=4b时,求函数f(x)+g(x)的单调区间,并求其在区间(-∞,-1]上的最大值.
解:(1)f′(x)=2ax,g′(x)=3x2+b.
因为曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处具有公共切线,所以
f(1)=g(1),且f′(1)=g′(1).
即a+1=1+b,且2a=3+b,解得a=3,b=3.
(2)记h(x)=f(x)+g(x).当b=a2时,h(x)=x3+ax2+a2x+1,h′(x)=3x2+2ax+a2.
令h′(x)=0,得x1=-,x2=-.
a>0时,h(x)与h′(x)的情况如下:
x
-
-
h′(x)
+
0
-
0
+
h(x)
所以函数h(x)的单调递增区间为和;单调递减区间为.
当-≥-1,即0
6时,函数h(x)在区间内单调递增,在区间内单调递减,在区间上单调递增,
又因h-h(-1)=1-a+a2=(a-2)2>0,
所以h(x)在区间(-∞,-1]上的最大值为h=1.
4.[2012·浙江卷] 已知a>0,b∈R,函数f(x)=4ax3-2bx-a+b.(1)证明:当0≤x≤1时,
(i)函数f(x)的最大值为|2a-b|+a;(ii)f(x)+|2a-b|+a≥0;(2)若-1≤f(x)≤1对x∈[0,1]恒成立,求a+b的取值范围.
解:(1)(i)f′(x)=12ax2-2b=12a.
当b≤0时,有f′(x)≥0,此时f(x)在[0,+∞)上单调递增.
当b>0时,f′(x)=12a.
此时f(x)在上单调递减,在上单调递增.
所以当0≤x≤1时,f(x)max=max{f(0),f(1)}=max{-a+b,3a-b}==|2a-b|+a.
(ii)由于0≤x≤1,故当b≤2a时,
f(x)+|2a-b|+a=f(x)+3a-b=4ax3-2bx+2a≥4ax3-4ax+2a=2a(2x3-2x+1).
当b>2a时,
f(x)+|2a-b|+a=f(x)-a+b=4ax3+2b(1-x)-2a>4ax3+4a(1-x)-2a=2a(2x3-2x+1).
设g(x)=2x3-2x+1,0≤x≤1,则g′(x)=6x2-2=6,
于是
x
0
1
g′(x)
-
0
+
g(x)
1
减
极小值
增
1
所以,g(x)min=g=1->0.所以当0≤x≤1时,2x3-2x+1>0.
故f(x)+|2a-b|+a≥2a(2x3-2x+1)≥0.
(2)由(i)知,当0≤x≤1时,f(x)max=|2a-b|+a,所以|2a-b|+a≤1.
若|2a-b|+a≤1,则由②知f(x)≥-(|2a-b|+a)≥-1.
所以-1≤f(x)≤1对任意0≤x≤1恒成立的充要条件是
即或③
在直角坐标系aOb中,③所表示的平面区域为如图所示的阴影部分,其中不包括线段BC.
做一组平行线a+b=t(t∈R),得-1<a+b≤3.
所以a+b的取值范围是(-1,3].
5.[2012·课标全国卷] 某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售.如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进16枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式;
(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
日需求量n
14
15
16
17
18
19
20
频数
10
20
16
16
15
13
10
以100天记录的各需求量的频率作为各需求量发生的概率.
①若花店一天购进16枝玫瑰花,X表示当天的利润(单位:元),求X的分布列、数学期望及方差;
②若花店计划一天购进16枝或17枝玫瑰花,你认为应购进16枝还是17枝?请说明理由.
解:(1)当日需求量n≥16时,利润y=80.
当日需求量n<16时,利润y=10n-80.
所以y关于n的函数解析式为
y=(n∈N).
(2)①X可能的取值为60,70,80,并且
P(X=60)=0.1,P(X=70)=0.2,P(X=80)=0.7.
X的分布列为
X
60
70
80
P
0.1
0.2
0.7
X的数学期望为EX=60×0.1+70×0.2+80×0.7=76.
X的方差为DX=(60-76)2×0.1+(70-76)2×0.2+(80-76)2×0.7=44.
②答案一:
花店一天应购进16枝玫瑰花.理由如下:
若花店一天购进17枝玫瑰花,Y表示当天的利润(单位:元),那么Y的分布列为
Y
55
65
75
85
P
0.1
0.2
0.16
0.54
Y的数学期望为
EY=55×0.1+65×0.2+75×0.16+85×0.54=76.4.
Y的方差为DY=(55-76.4)2×0.1+(65-76.4)2×0.2+(75-76.4)2×0.16+(85-76.4)2×0.54
=112.04.
由以上的计算结果可以看出,DX0,所以零点在区间(0,1)上,选C
【温馨提示】函数零点附近函数值的符号相反,这类选择题通常采用代入排除的方法求解。
11.(2010天津理)(8)若函数f(x)=,若f(a)>f(-a),则实数a的取值范围是
(A)(-1,0)∪(0,1) (B)(-∞,-1)∪(1,+∞)
(C)(-1,0)∪(1,+∞) (D)(-∞,-1)∪(0,1)
【答案】C
【解析】本题主要考查函数的对数的单调性、对数的基本运算及分类讨论思想,属于中等题。
由分段函数的表达式知,需要对a的正负进行分类讨论。
【温馨提示】分类函数不等式一般通过分类讨论的方式求解,解对数不等式既要注意真数大于0,同事要注意底数在(0,1)上时,不等号的方向不要写错。
12.(2010天津理)(2)函数f(x)=的零点所在的一个区间是
(A)(-2,-1)(B)(-1,0)(C)(0,1)(D)(1,2)
【答案】B
【解析】本题主要考查函数零点的概念与零点定理的应用,属于容易题。
由及零点定理知f(x)的零点在区间(-1,0)上。
【温馨提示】函数零点附近函数值的符号相反,这类选择题通常采用代入排除的方法求解。
13.(2010福建文)7.函数的零点个数为 ( )
A.3 B.2 C.1 D.0
【答案】B
【解析】当时,令解得;
当时,令解得,所以已知函数有两个零点,选C。
【命题意图】本题考查分段函数零点的求法,考查了分类讨论的数学思想。
14.(2010湖北文)3.已知函数,则
A.4 B. C.-4 D-
【答案】B
【解析】根据分段函数可得,则,
所以B正确.
二、填空题
1.(2010上海文)14.将直线、、(,)围成的三角形面积记为,则 。
【答案】
【解析】B 所以BO⊥AC,
=
所以
2.(2010湖南文)10.已知一种材料的最佳加入量在100g到200g之间,若用0.618法安排试验,则第一次试点的加入量可以是 g
【答案】171.8或148.2
【解析】根据0.618法,第一次试点加入量为
110+(210-110)0.618=171.8
或 210-(210-110)0.618=148.2
【命题意图】本题考察优选法的0.618法,属容易题。
3.(2010陕西文)13.已知函数f(x)=若f(f(0))=4a,则实数a= .
答案 2
【解析】f(0)=2,f(f(0))=f(2)=4+2a=4a,所以a=2
4.(2010重庆理)(15)已知函数满足:,,则=_____________.
解析:取x=1 y=0得
法一:通过计算,寻得周期为6
法二:取x=n y=1,有f(n)=f(n+1)+f(n-1),同理f(n+1)=f(n+2)+f(n)
联立得f(n+2)= —f(n-1) 所以T=6 故=f(0)=
5.(2010天津文)(16)设函数f(x)=x-,对任意x恒成立,则实数m的取值范围是________
【答案】m<-1
【解析】本题主要考查了恒成立问题的基本解法及分类讨论思想,属于难题。
已知f(x)为增函数且m≠0
若m>0,由复合函数的单调性可知f(mx)和mf(x)均为增函数,此时不符合题意。
M<0,时有因为在上的最小值为2,所以1+即>1,解得m<-1.
【温馨提示】本题是较为典型的恒成立问题,解决恒成立问题通常可以利用分离变量转化为最值的方法求解。
6.(2010浙江文)(16) 某商家一月份至五月份累计销售额达3860万元,预测六月份销售额为500万元,七月份销售额比六月份递增x%,八月份销售额比七月份递增x%,九、十月份销售总额与七、八月份销售总额相等,若一月至十月份销售总额至少至少达7000万元,则,x 的最小值 。
答案 20
7.(2010天津理数)(16)设函数,对任意,恒成立,则实数的取值范围是 .
【解析】本题主要考查函数恒成立问题的基本解法,属于难题。
依据题意得在上恒定成立,即在上恒成立。
当时函数取得最小值,所以,即,解得或
【温馨提示】本题是较为典型的恒成立问题,解决恒成立问题通常可以利用分离变量转化为最值的方法求解
8.(2010广东文数)
9.(2010江苏卷)11、已知函数,则满足不等式的x的范围是_____。
【解析】 考查分段函数的单调性。
三、解答题
1.(2010福建文)21.(本小题满分12分)
某港口要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口北偏西30°且与该港口相距20海里的处,并正以30海里/小时的航行速度沿正东方向匀速行驶。假设该小艇沿直线方向以海里/小时的航行速度匀速行驶,经过小时与轮船相遇。
(Ⅰ)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(Ⅱ)为保证小艇在30分钟内(含30分钟)能与轮船相遇,试确定小艇航行速度的最小值;
(Ⅲ)是否存在,使得小艇以海里/小时的航行速度行驶,总能有两种不同的航行方向与轮船相遇?若存在,试确定的取值范围;若不存在,请说明理由。
2.(2010湖北文)19.(本小题满分12分)
已知某地今年年初拥有居民住房的总面积为a(单位:m2),其中有部分旧住房需要拆除。当地有关部门决定每年以当年年初住房面积的10%建设新住房,同事也拆除面积为b(单位:m2)的旧住房。
(Ⅰ)分别写出第一年末和第二年末的实际住房面积的表达式:
(Ⅱ)如果第五年末该地的住房面积正好比今年年初的住房面积增加了30%,则每年拆除的旧住房面积b是多少?(计算时取1.15=1.6)
2009年高考题
1.(2009福建卷文)若函数的零点与的零点之差的绝对值不超过0.25, 则可以是
A. B.
C. D.
答案 A
解析 的零点为x=,的零点为x=1, 的零点为x=0, 的零点为x=.现在我们来估算的零点,因为g(0)= -1,g()=1,所以g(x)的零点x(0, ),又函数的零点与的零点之差的绝对值不超过0.25,只有的零点适合,故选A。
2.(2009山东卷文)若函数f(x)=a-x-a(a>0且a1)有两个零点,则实数a的取值范围是 .
答案
解析 设函数且和函数,则函数f(x)=a-x-a(a>0且a1)有两个零点, 就是函数且与函数有两个交点,由图象可知当时两函数只有一个交点,不符合,当时,因为函数的图象过点(0,1),而直线所过的点(0,a)一定在点(0,1)的上方,所以一定有两个交点.所以实数a的取值范围是.
【命题立意】:本题考查了指数函数的图象与直线的位置关系,隐含着对指数函数的性质的考查,根据其底数的不同取值范围而分别画出函数的图象进行解答
3.(2009山东卷理)(本小题满分12分)
两县城A和B相距20km,现计划在两县城外以AB为直径的半圆弧上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k ,当垃圾处理厂建在的中点时,对城A和城B的总影响度为0.065.
(1)将y表示成x的函数;
(11)讨论(1)中函数的单调性,并判断弧上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由。
A
B
C
x
解法一:(1)如图,由题意知AC⊥BC,,
其中当时,y=0.065,所以k=9
所以y表示成x的函数为
(2),,令得,所以,即,当时, ,即所以函数为单调减函数,当时,
,即所以函数为单调增函数.所以当时, 即当C点到城A的距离为时, 函数有最小值.
解法二: (1)同上.
(2)设,
则,,所以
当且仅当即时取”=”.
下面证明函数在(0,160)上为减函数, 在(160,400)上为增函数.
设04×240×240
9 m1m2<9×160×160所以,
所以即函数在(0,160)上为减函数.
同理,函数在(160,400)上为增函数,设1609×160×160
所以,
所以即函数在(160,400)上为增函数.
所以当m=160即时取”=”,函数y有最小值,
所以弧上存在一点,当时使建在此处的垃圾处理厂对城A和城B的总影响度最小.
【命题立意】:本题主要考查了函数在实际问题中的应用,运用待定系数法求解函数解析式的 能力和运用换元法和基本不等式研究函数的单调性等问题.
5. (2009湖南卷理)(本小题满分13分)
某地建一座桥,两端的桥墩已建好,这两墩相距米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为256万元,距离为米的相邻两墩之间的桥面工程费用为万元。假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为万元。
(Ⅰ)试写出关于的函数关系式;
(Ⅱ)当=640米时,需新建多少个桥墩才能使最小?
解 (Ⅰ)设需要新建个桥墩,
所以
(Ⅱ) 由(Ⅰ)知,
令,得,所以=64
当0<<64时<0, 在区间(0,64)内为减函数;
当时,>0. 在区间(64,640)内为增函数,
所以在=64处取得最小值,此时,
故需新建9个桥墩才能使最小。
6.(2009年上海卷理)有时可用函数
描述学习某学科知识的掌握程度,其中x表示某学科知识的学习次数(),表示对该学科知识的掌握程度,正实数a与学科知识有关。
(1)证明 当时,掌握程度的增加量总是下降;
(2)根据经验,学科甲、乙、丙对应的a的取值区间分别为
,,。当学习某学科知识6次时,掌握程度是85%,请确定相应的学科。
证明 (1)当
而当,函数单调递增,且>0……..3分
故单调递减
当,掌握程度的增长量总是下降……………..6分
(2)由题意可知0.1+15ln=0.85……………….9分
整理得
解得…….13分
由此可知,该学科是乙学科……………..14分
7.(2009上海卷文)
(本题满分16分)本题共有2个小题,第1小题满分6分,第2小题满分10分 .有时可用函数
描述学习某学科知识的掌握程度.其中表示某学科知识的学习次数(),表示对该学科知识的掌握程度,正实数a与学科知识有关.
(1)证明:当x 7时,掌握程度的增长量f(x+1)- f(x)总是下降;
(2)根据经验,学科甲、乙、丙对应的a的取值区间分别为(115,121],(121,127],
(127,133].当学习某学科知识6次时,掌握程度是85%,请确定相应的学科.
证明 (1)当时,
而当时,函数单调递增,且
故函数单调递减
当时,掌握程度的增长量总是下降
(2)有题意可知
整理得
解得…….13分
由此可知,该学科是乙学科……………..14分
2008年高考题
一、选择题
1.(2008年全国一2)汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一
过程中汽车的行驶路程看作时间的函数,其图像可能是 ( )
s
t
O
A.
s
t
O
s
t
O
s
t
O
B.
C.
D.
答案 A
2.(2008年福建卷12)已知函数y=f(x),y=g(x)的导函数的图象如下图,那么y=f(x),y=g(x)
的图象可能是 ( )
答案 D
3.(07广东)客车从甲地以60km/h的速度匀速行驶1小时到达乙地,在乙地停留了半小时,然后以80km/h的速度匀速行驶1小时到达丙地,下列描述客车从甲地出发.经过乙地,最后到达丙地所经过的路程s与时间t之间关系的图象中,正确的是 ( )
A B C D
答案 C
4.某地一年内的气温(单位:℃)与时刻(月份)之间的关系如图所示,已知该年的平均气温为10℃ .令C(t)表示的时间段[0,t]的平均气温,
C(t)与t之间的函数关系用下列图象表示,则正确的应该是 ( )
答案 A
解析 由图可以发现当t=6时,C(t)=0,排除C;t=12时,C(t)=10,排除D;t在大于6 的某一段气温超于10,所以排除B,故选A。
二、填空题
6.(2007年上海4)方程 的解是 .
答案
三、解答题
8.(2008年江苏卷17)某地有三家工厂,分别位于矩形ABCD
的顶点A,B 及CD的中点P处,已知AB=20km,CB=10km ,
为了处理三家工厂的污水,现要在矩形ABCD 的区域上
(含边界),且A,B与等距离的一点O 处建造一个
污水处理厂,并铺设排污管道AO,BO,OP,设排污管道的总长
为km.
(Ⅰ)按下列要求写出函数关系式:
①设∠BAO=(rad),将表示成的函数关系式;
②设OP(km) ,将表示成的函数关系式.
(Ⅱ)请你选用(Ⅰ)中的一个函数关系式,确定污水处理厂的位置,使三条排污管道总长度最短.
解 本小题主要考查函数最值的应用.
(Ⅰ)①设AB中点为Q,由条件知PQ 垂直平分AB,若∠BAO=(rad) ,则
, 故,又OP=,
所以,
所求函数关系式为
②若OP=(km) ,则OQ=10-,所以OA=OB=
所求函数关系式为
(Ⅱ)选择函数模型①,
令得sin,因为,所以=.当时,,是
的减函数;当时,,y是的增函数.所以当=时,(km)。这时点0位于线段AB 的中垂线上,且距离AB边km处。
9.(2008年湖北卷20).(本小题满分12分)水库的蓄水量随时间而变化.现用表示时间,以月为单位,年初为起点.根据历年数据,某水库的蓄水量(单位:亿立方米)关于的近似函数关系式为
(Ⅰ)该水库的蓄求量小于50的时期称为枯水期.以表示第i月份(),问一年内哪几个月份是枯水期?
(Ⅱ)求一年内该水库的最大蓄水量(取计算).
解 (1)①当0<t10时,V(t)=(-t2+14t-40)
化简得t2-14t+40>0,
解得t<4,或t>10,又0<t10,故0<t<4.
②当10<t12时,V(t)=4(t-10)(3t-41)+50<50,
化简得(t-10)(3t-41)<0,
解得10<t<,又10<t12,故 10<t12.
综上得00时,f(x)>1,且对任意的a、b∈R,有f(a+b)=f(a)f(b),
求证:f(0)=1;
求证:对任意的x∈R,恒有f(x)>0;
(3)证明:f(x)是R上的增函数;
(4)若f(x)·f(2x-x2)>1,求x的取值范围。
解 (1)令a=b=0,则f(0)=[f(0)]2∵f(0)≠0 ∴f(0)=1
(2)令a=x,b=-x则 f(0)=f(x)f(-x) ∴
由已知x>0时,f(x)>1>0,当x<0时,-x>0,f(-x)>0
∴又x=0时,f(0)=1>0
∴对任意x∈R,f(x)>0
(3)任取x2>x1,则f(x2)>0,f(x1)>0,x2-x1>0
∴
∴f(x2)>f(x1) ∴f(x)在R上是增函数
(4)f(x)·f(2x-x2)=f[x+(2x-x2)]=f(-x2+3x)又1=f(0),
f(x)在R上递增
∴由f(3x-x2)>f(0)得:3x-x2>0 ∴ 0
查看更多