高一数学同步辅导教材(第7讲)

高一数学同步辅导教材(第7讲)

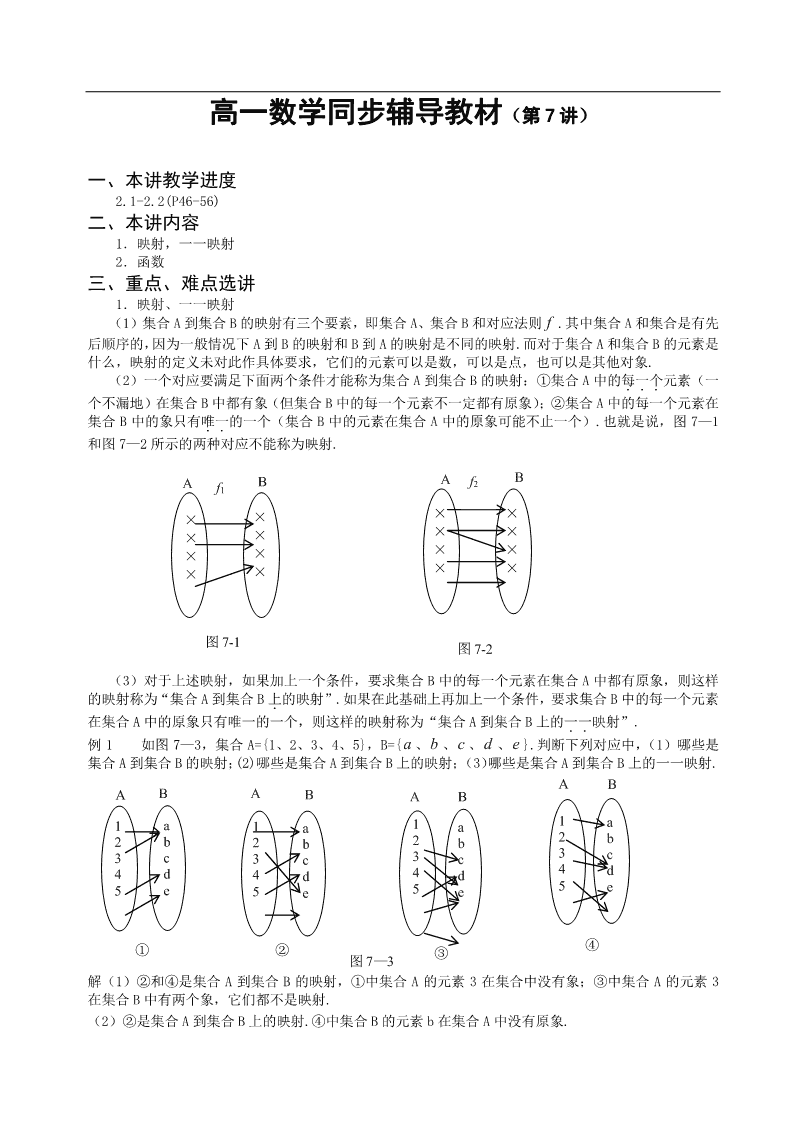
高一数学同步辅导教材（第 7 讲） 一、本讲教学进度 2.1-2.2(P46-56) 二、本讲内容 1．映射，一一映射 2．函数 三、重点、难点选讲 1．映射、一一映射 （1）集合 A 到集合 B 的映射有三个要素，即集合 A、集合 B 和对应法则 f .其中集合 A 和集合是有先 后顺序的，因为一般情况下 A 到 B 的映射和 B 到 A 的映射是不同的映射.而对于集合 A 和集合 B 的元素是 什么，映射的定义未对此作具体要求，它们的元素可以是数，可以是点，也可以是其他对象. （2）一个对应要满足下面两个条件才能称为集合 A 到集合 B 的映射：①集合 A 中的每一个．．．元素（一 个不漏地）在集合 B 中都有象（但集合 B 中的每一个元素不一定都有原象）；②集合 A 中的每一个元素在 集合 B 中的象只有唯一．．的一个（集合 B 中的元素在集合 A 中的原象可能不止一个）.也就是说，图 7—1 和图 7—2 所示的两种对应不能称为映射. （3）对于上述映射，如果加上一个条件，要求集合 B 中的每一个元素在集合 A 中都有原象，则这样 的映射称为“集合 A 到集合 B 上．的映射”.如果在此基础上再加上一个条件，要求集合 B 中的每一个元素 在集合 A 中的原象只有唯一的一个，则这样的映射称为“集合 A 到集合 B 上的一一．．映射”. 例 1 如图 7—3，集合 A={1、2、3、4、5}，B={ a 、b 、c 、 d 、e }.判断下列对应中，（1）哪些是 集合 A 到集合 B 的映射；(2)哪些是集合 A 到集合 B 上的映射；（3）哪些是集合 A 到集合 B 上的一一映射. 解（1）②和④是集合 A 到集合 B 的映射，①中集合 A 的元素 3 在集合中没有象；③中集合 A 的元素 3 在集合 B 中有两个象，它们都不是映射. （2）②是集合 A 到集合 B 上的映射.④中集合 B 的元素 b 在集合 A 中没有原象. 图 7—3 1 2 3 4 5 a b c d e A B ① 1 2 3 4 5 a b c d e B A ② 1 2 3 4 5 a b c d e B A ③ 1 2 3 4 5 a b c d e B A ④ A B × × × × × × × × 图 7-1 A B × × × × × × × × 图 7-2 f1 f2 （3）②是集合 A 到集合 B 上的一一映射. 例 2 已知集合 A={ 30  xx }，B={ 10  yy } .判断下列各对应 f 是否是集合 A 到集合 B 的映 射？一一映射？并说明理由. (1) f : xyx 3 1 ； (2) : xyx 4 1 ； (3) : 2)2(  xyx ； (4) : 2 9 1 xyx  ； (5) : 2)1(4 1  xyx 解 （1）∵ 30  x ， ∴ 13 10  x . 因此对集合 A 的每一个元素 x ， Bxy  3 1 ，所以对应 : BA 是集合 A 到集合 B 的映射. 对于集合 B 中的每一个元素 y ，由 yx 3 及 10  y ，有 30,330  xy .即集合 B 中的每一个元素在集合 A 中都有原象，且这样的原象只有一个，所以 对应 : 是一一映射. （2）∵ 30  x ， ∴ 4 3 4 10  x .所以对于集合 A 中的每一个元素 x ，在集合 B 中都有唯 一的象，因此对应 : 是映射. 而集合 B 中有些元素，如 1y ，在集合 A 中没有原象，因此映射 : 不是一一映射. （3）∵ ， ∴ 122  x ， ∴ 4)2(0 2  x .由此知集合 A 的某些元 素，如 0x ，在集合 B 中没有象，因此对应 : 不是映射，更不是一一映射. （4）∵ ， ∴ 19 10 2  x .因此对于集合 A 中的每一个元素 x ，在集合 B 中都有唯 一的象，所以对应 : 是映射. 由 2 9 1 xy  ，对于集合 B 中的每一个元素 y ， Ayx  3 ，即集合 B 中的每一个元素在集合 A 中有唯一的原象，因此映射 : 是一一映射. （5）集合 A 中的每一个元素在集合 B 中都有唯一的象.对于集合 A 中的元素 0x 和 2x ，都对 应于集合 B 中的同一个元素 4 1 ，所以对应 : 是映射，但不是一一映射. 2.函数 （1）函数的定义. 在初中学过的函数概念是从运动变化的角度出发，用变量来定义的，习惯上称为传统定义.传统定 义由研究变量的物理意义而产生，反映了两个变量之间变化的相依关系.由于受变量物理意义的限制，对 某些函数难以进行研究，因为有些函数从物理的角度不好解释.因此高中学习函数时重新引进了用映射刻 划函数的近代定义，它更具有一般性.当然，两种定义的本质是一样的. 集合 A 到集合 B 的映射 : 要成为函数，还必须满足两个条件：①集合 A、B 都是非空集 合；②集合 A、B 都是数的集合.其中集合 A 就是函数的定义域，而集合 B 不一定是值域.一般地说，值域 C 是集合 B 的子集，即 BC  .（若集合 BC  ，则这个映射就成为集合 A 到集合 B 上的映射）. （2）函数的三要素. 定义域 A，值域 C 和定义域 A 到值域 C 的对应法则 ，构成了函数的三个要素.当且仅当这三个要 素完全相同时，两个函数才是同一个函数. 在判断两个函数是否同一函数时，主要观察它们的定义域和 对应法则是否相同. （3）区间 设 a 、 Rb ，且 ba  .用闭区间[ ba, ]表示集合{ bxax  }，用开区间 ),( ba 表示集合 { bxax  }，用半开半闭区间 ],( ba 表示集合{ bxax  }，用半开半闭区间 ),[ ba 表示集合 { bxax  }. （4）函数的表示法. 函数常用的表示法有：解析法，列表法及图像法，三种表示法各有其长处. 要搞清符号 )(xf 和 )(af （ a 为常数）的区别.一般情况下， 是一个随自变量 x 的变化而 变化的变量，而 是当自变量 ax  时函数的值，是一个确定的量. 与初中接触到的函数不一样，这里的函数可以是在不同区间中（或不同条件下）表达式不同的分 段函数，因此函数的图像也不一定是一条平滑曲线，它可能是一些孤立的点，一些线段，或一些曲线. 例 3 判断下列各对函数是否是同一个函数，并说明理由. (1) 2)( xxf  ， 2)()( xxg  ； (2) .)( 3 3xxf  ， xxg )( ； (3) 1 1)( 2   x xxf ， 1)(  xxg ； (4) 1)(  xxf ，      );1(,1 ),1(,1)( xx xxxg (5) ， ； (6) 21)( xxf  ， 21)( ttg  . 解 （1）不是同一个函数，两者的定义域不同， 它们的定义域分别为 ),(  和 ),0[  . （2）不是同一个函数，它们的对应法则和值域都不同. xxf )( ，其值域为 ； ，其值域为 . （3）不是同一个函数，它们的定义域不同.定义域分别为 ),1()1,(   和 . （4）不是同一个函数，它们的定义域不同，定义域分别是 和 ),1()1,(   . （5）是同一个函数， )()( xgxxf  . （6）是同一个函数，虽然自变量用不同的字母表示，但定义域、值域和对应法则都相同. 例 4 已知 32)(  xxf ， 12)( 2  xxg ，求 )]([ xgf 和 )]([ xfg . 解 = 143)12(23)(2 22  xxxg . = 192481)32(21)]([2 222  xxxxf . 评析 由此可见，在求 时，只要用 )(xg 代替 )(xf 表达式中的 x ，然后再将 )(xg 的表达 式代入其中，就可以求得 .一般来说， )]([)]([ xfgxgf  . 例5 （1）已知 )(xf       ,12 ,2 ,0 2x (x > 0), (x = 0), (x < 0), 求 )2(f ， )1(f ， )]0([ ff ， )]2 2([ ff ； （2）已知           ),2(,23 ),21(, ),1(,32 )( 2 xx xx xx xg 且 3)( tg ， 求t . 解 （1）∵ 02  ， ∴ 0)2( f . ∵ 01 ， ∴ 11)1(2)1( 2 f . 0)2()]0([  fff . 2)0(]1)2 2(2[)2 2([ 2  ffff . (2)当 132)(,1  xxgx ； 当 40,21 2  xx ；当 423)(,2  xxgx . .3),2,1(3 .3,3)(,3)( 2   t tttgtg   例 6 （1）画出函数 342  xxy 的图像； （2）画出函数 342  xxy 的图像； （3）已知函数 )(xfy  的图像如图 7—4， 写出 )(xf 的解析式. 解 （1）      ).0(,1)2( ),0(,1)2(34 2 2 2 xx xxxxy 图 7—4 图像如图 7—5. (2)当 0342  xx ,即 1x 或 3x 时， 1)2(34 22  xxxy ； 当 0342  xx ，即 31  x 时， 1)2(34)34( 222  xxxxxy . ∴      ).31(,1)2( ),3,1(,1)2( 2 2 xx xxxy 或 图像如图 7—6. （3）      ).10(, ),01(,1 xx xxy 0 1 1 -1 -1 y x 0 1 2 3-1-2-3 -1 1 2 3 x y 图7—5 -1 0 1 1 2 3 x 3 2 y 图7—6 评析 （1）对于含有绝对值的函数的图像，通常先用零点分区间法得出函数的解析式，然后以分段 函数的形式写出函数的解析式，再画出函数的图像. （2）由第（2）题可见，画 )(xfy  的图像，只要把 )(xfy  的图像在 x 轴下方部分“翻到” 轴上方，即作出这一部分图像关于 轴的对称曲线，而在 轴上方的曲线保持不变，就可以得到函数 )(xfy  的图像. （3）函数的定义域如果没有特别说明，通常指使式子有意义的一切自变量 的集合，在实际问题中， 还应考虑自变量 要满足的实际问题的条件. 我们现在涉及到的使式子有意义的情况，仅是分母不能为零，负数不能开偶次方.今后学习了其他 函数，还会出现另外一些情况. 例 7 求下列函数的定义域： （1） 23 1 2  xxy ； （2） x y 21 21 1    ； （3） 752 2  xxy . 解 （1） .21,0)2)(1(,0232  xxxxxx 且 ∴定义域为 Rxxxx  ,2,1 且 . （2）由 ;0,2 xx 由 2 2 21 2   x x x , 2x ； 由 2 23 2 2121 21     x x x x x , 3 2x . ∴定义域为    Rxxxxx ,3 2,2,0 且且 . （3） 2 71,0)72)(1(,0752 2  xxxxxx 或 . ∴定义域为 }2 7,1{  xxx 或 . 评析 对于繁分式，一条分数线即有一个限制条件，本题有三条分数线，因此有三个限制条 件. 例 8 已知函数 的定义域为[-1，2]，求函数 )1()1()(  xfxfxg 的定义域. 解 由 )(xf 中的 x 必须满足 21  x ，因此 )(xg 中的 必须满足：      ,211 ,211 x x 即      .30 ,12 x x ∴ )(xg 的定义域为  10  xx . 例 9 （1）已知 11)11( 2  xxf ，求 )(xf ； （2）已知函数 的定义域是 ),0()0,(   ，且 xxfxf 4)1(2)(3  ，求 ； (3)已知 32)2(  xxf ，求 . 解 （1）设 xt 11 ，则 11  tx )1( t ， ∴ ttttf 21)1()( 22  ， ∴ xxxf 2)( 2  )1( x . （2）由 xxfxf 4)1(2)(3  ， ① 将 x 换成 x 1 ， 得 xxfxf 4)(2)1(3  ， ② 3×①－2×② ，得 xxxf 812)(5  ， ∴ xxxf 5 8 5 12)(  . (x≠0) （3）令 2 xt ，则 2,)2( 2  ttx . ∴ )2(11823)2(2)( 22  tttttf . ∴ ).2(1182)( 2  xxxxf 例 10 设      ),0(,,1 ),0(,1)( x xxf 画出函数 )1(  xfy 的图像. 解 由已知，       ),01(,1 ),01(,1 )1( x x xf ∴       ).1(,1 ),1(,1 x x y 图像如图 7—7 所示. 练习 一、选择题 1．设 f 是从集合 A 到集合 B 的映射，下列四个说法：①集合 A 中的每一个元素在集合 B 中都有象； ②集合 B 中的每一个元素在集合 A 中都有原象；③集合 A 中不同的元素在集合 B 中的象也不同；④集合 B 中不同的元素在集合 A 中的原象也不同，其中正确的是 （ ） A．①和② B．②和③ C．③和④ D．①和④ 2．已知集合 A= 60  xx ，B= 30  yy ，则下列对应关系 f 中，不能看成是从集合 A 到 -1 1 0 1 2 x y -1 图7—7 集合 B 的映射的是 （ ） A． f ： xyx 2 1 B． ： xyx 3 1 C． ： xyx  D． ： xyx 6 1 3．下列三个命题：①函数是从定义域到值域的一一映射；②函数的定义域和值域可能是数集，也可 能不是数集；③函数的定义域和值域都不能是空集.其中真命题是 （ ） A．① B．② C．③ D．①和③ 4 ． 下 列 各 组 函 数 ： ① 2)(  xxf ， 44)( 2  xxxg ；② 1 1)( 2   x xxf ， 1)(  xxg ；③ xxf )( ， x xxg )( ；④ 1)(  xxf ，       )0(,1 )0(,1 )( xx xx xg .其 中 )(xf 和 )(xg 表示同一个函数的是 （ ） A．① B．①和② C．③ D．④ 5．函数 xxy  1 的定义域是 （ ） A． ),0()0,(   B． ),1()1,0()0,(   C． )0,1()1,(   D． )0,( 6．已知函数 )(xf 的定义域是 )1,0( ，则函数 )1( 2 xf 的定义域为 （ ） A． )2,1( B． )2,1()1,2(  C． )0,1( D． )1,0()0,1(  二、填空题 7．已知 ),( yx 在映射 f 下的象是 )2,2( yxyx  ，则 )3,1( 在 下的原象 是 。 8．函数 xx xxf  1)( 2 的定义域是 。 9．已知          )0(,0 )0(,2 )0(, )( 3 x x xx xf 则 )2(f ，  )2(f ，  )]6([ ff . 10．已知 xx xf   )1 1( ，则 )(xf . 三、解答题 11．求下列函数的定义域： （1） xxx xy   2 1 ； （2） 52 62   x xxy . 12．若 13:  xyf 是从集合 A= },3,2,1{ k 到集合 B= }3,,7,4{ 24 aaa  的一个映射，求自然数 a 和 k 的值及集合 A 和 B. 13．若函数 34 31 2 3   mxmx xy 的定义域为 R ，求实数 m 的取值范围. 14．已知 32)( 2  xxxf ，作函数 2 )()()( xfxfxg  的图像. 答案与提示 [答案] 一、1．D 2．C 3．C 4．A 5．D 6．B 二、7． )1,1(  8． )0,( 9．8，0，2 10． )1(1 1   xx x 三、11．（ 1） )2,0[ ， （2） ),3(]2,7()7,(   12． }16,10,7,4{},5,3,2,1{,5,2  BAka 13． 4 30  m 14．      ).13(0 ),1,3(,4)1()( 2 x xxxxg 或 [提示] 一、6． )2,1()1,2(,21,110 22  xxx 二、7．由      ,32 ,12 yx yx 解得      .1 ,1 y x 10．令 ,1 211 1   xx xt 则 )1(1 1)(,1 1)(,1 1,1     xx xxft ttft txt 三、11．（ 1）由       ,0 ,02 1 xx x x      ,0 ,21 x x 20  x . （2）由      ,052 ,062 x xx      ,3,7 ,3,2 xx xx 且 或 3,7,2  xxx 或且 12．∵ 4113  ， 7123  ， ∴(Ⅰ)      ,133 ,133 2 4 kaa a 或 （Ⅱ）      .1333 ,13 2 4 aa ka 由 ( Ⅰ ) ， 10,,10 44  aNaa  舍去. 由 （ Ⅱ ）， 5,2,01032  aaa （舍去），∴ 5,213 4  kk 13． .0342  mxmx （1）若 ;0334,0 2  mxmxm （2）若 ,0m △= .4 30.4 30,034)4( 2  mmmm 14．当 0)( xf ，即 0322  xx ， 13  x ， .0)( xg 当 0)( xf ，即 3x 或 1x ， 4)1()()( 2  xxfxg . 图像如右. y=g(x)y x0-1-2-3 1 2 1 2 -1 -2