北京市昌平区新学道临川学校2019-2020学年高二上学期期中考试数学（理）试题

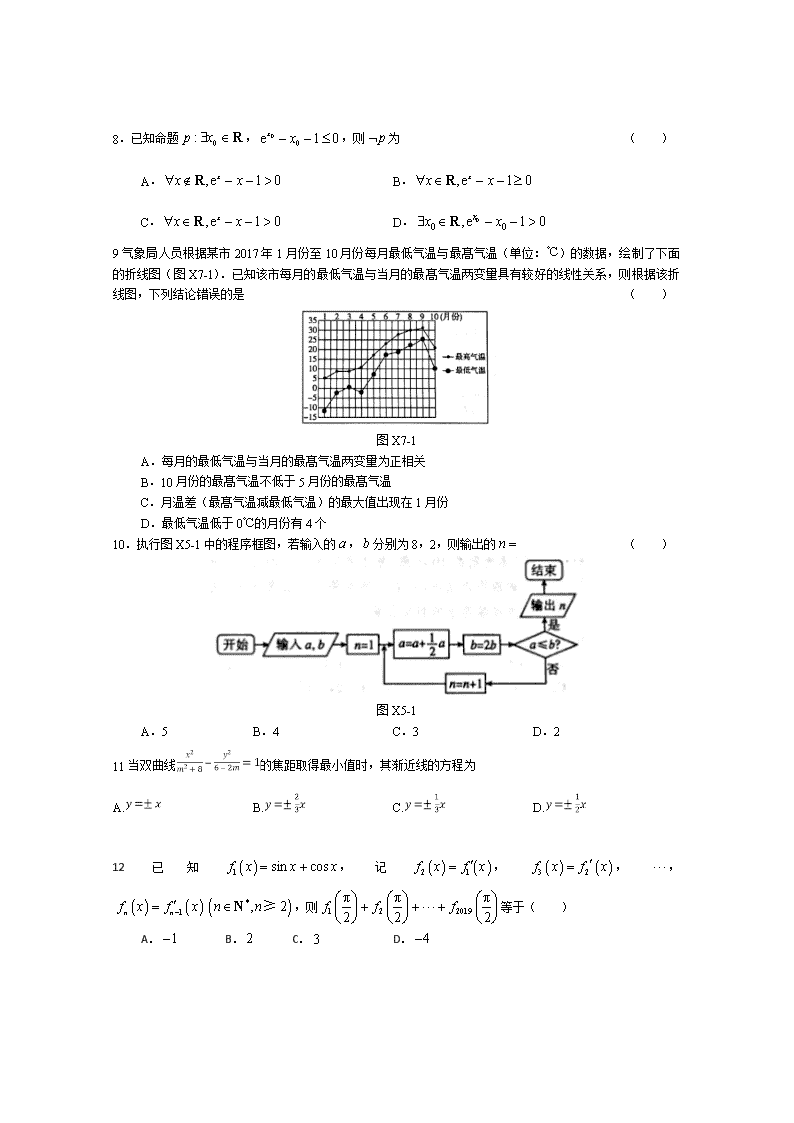
北京市昌平区新学道临川学校2019-2020学年高二上学期期中考试数学（理）试题

北京新学道临川学校2019-2020学年度高二上期期中试卷 数学试题（理科） 满分；150分 时间；120分钟 一、 选择题（共12小题，每小题5分，共60分，在每小题列出的四个选项中，选出符合题目要求的一项）‎ ‎1函数的导函数为（ ）‎ A． B．‎ C． D．‎ ‎2图X3-1是一个边长为4的正方形二维码，为了测算图中黑色部分的面积，在正方形区域内随机投掷400个点，其中落入黑色部分的有225个点，据此估计黑色部分的面积为 （ ）‎ 图X3-1‎ A．8 B．‎9 ‎C．10 D．12‎ ‎3已知圆与抛物线的准线相切，则的值为 （ ）‎ A．0 B．‎2 ‎C．0或1 D．0或2‎ ‎4某中学有高中生960人，初中生480人，为了了解学生的身体状况．采用分层抽样的方法．从该校学生中抽取容量为的样本，其中高中生抽取了24人，那么等于 （ ）‎ A．12 B．‎18 ‎C．24 D．36‎ ‎5某同学先后投掷一枚骰子两次，第一次向上的点数记为，第二次向上的点数记为．在平面直角坐标系中，以为坐标的点在直线上的概率为 （ ）‎ A． B． C． D．‎ ‎6设，则“”是“直线与直线平行”的 （ ）‎ A．充要条件 B．必要不充分条件 ‎ C．充分不必要条件 D．既不充分也不必要条件 ‎7若双曲线的中心为原点，是双曲线的焦点，过的直线与双曲线相交于，两点，旦的中点为，则双曲线的方程为 （ ）‎ A． B． C． D．‎ ‎8．已知命题，，则为 （ ）‎ A． B．‎ C． D．‎ ‎9气象局人员根据某市2017年1月份至10月份每月最低气温与最髙气温（单位：℃）的数据，绘制了下面的折线图（图X7-1）．已知该市每月的最低气温与当月的最髙气温两变量具有较好的线性关系，则根据该折线图，下列结论错误的是 （ ）‎ 图X7-1‎ A．每月的最低气温与当月的最髙气温两变量为正相关 B．10月份的最髙气温不低于5月份的最髙气温 C．月温差（最髙气温减最低气温）的最大值出现在1月份 D．最低气温低于‎0℃‎的月份有4个 ‎10．执行图X5-1中的程序框图，若输入的，分别为8，2，则输出的 （ ）‎ 图X5-1‎ A．5 B．‎4 ‎C．3 D．2‎ ‎11当双曲线的焦距取得最小值时，其渐近线的方程为 A. B. C. D.‎ ‎12已知，记，，，，则等于（ ）‎ A． B． C． D．‎ 第二部分（非选择题 共90分）‎ 二、填空题：本大题共4小题，每小题5分，共20分．把答案填在答题卡上．‎ ‎13．已知样本容量为200，在样本的频率分布直方图中，共有个小矩形，若其中一个小矩形的面积等于其余个小矩形的面积的，则该小矩形对应的小组的频数为________．‎ ‎14．曲线在点处的切线方程为，则点的坐标是________．‎ ‎15设函数为可导函数，且满足条件，则曲线在点处的切线的斜率是________．‎ ‎16．已知双曲线的右焦点为，过点作双曲线的一条渐近线的垂线，垂足为，交另一条渐近线于，若，则双曲线的离心率________．‎ 三、解答题：本大题共6小题，共70分．17题10分，18-22题每题12分，解答应写出文字说明，演算步骤或证明过程．‎ ‎17．(10分)一个袋中装有四个形状大小完全相同的球，球的编号分别为1,2,3,4，‎ ‎(1)从袋中随机取出两个球，求取出的球的编号之和不大于4的概率；‎ ‎(2)先从袋中随机取一个球，该球的编号为m，将球放回袋中，然后再从袋中随机取一个球，该球的编号为n，求n＜m＋2的概率．‎ ‎18.已知p: ,q: ,若是的必要不充分条件，求实数m的取值范围。‎ ‎19已知函数及曲线上一点，过点作直线．‎ ‎（1）若直线与曲线相切于点，求直线的方程；‎ ‎（2）若直线与曲线相切，且切点异于点，求直线的方程．‎ ‎20已知椭圆C : , 经过点P，离心率是.‎ ‎(I) 求椭圆C的方程；‎ ‎(II) 设直线与椭圆交于两点，且以为直径的圆过椭圆右顶点，求证：直线l恒过定点．‎ ‎21一企业从某条生产线上随机抽取100件产品，测量这些产品的某项技术指标值x，得到如下的频率分布表：‎ x ‎[11，13)‎ ‎[13，15)‎ ‎[15，17)‎ ‎[17，19)‎ ‎[19，21)‎ ‎[21，23]‎ 频数 ‎2‎ ‎12‎ ‎34‎ ‎38‎ ‎10‎ ‎4‎ ‎（1）作出样本的频率分布直方图，并估计该项技术指标值x的平均数和众数；‎ ‎（2）若x<13或x≥21，则该产品不合格，现从不合格的产品中随机抽取2件，求抽取的2件产品中技术指标值小于13的产品恰有1件的概率。‎ ‎22已知抛物线C：y2=3x的焦点为F，斜率为的直线l与C的交点为A，B，与x轴的交点为P．‎ ‎（1）若，求l的方程；‎ ‎（2）若，求．‎