高中数学选修2-3教学课件：8_4独立性检验的思想及应用（二）

高中数学选修2-3教学课件：8_4独立性检验的思想及应用（二）

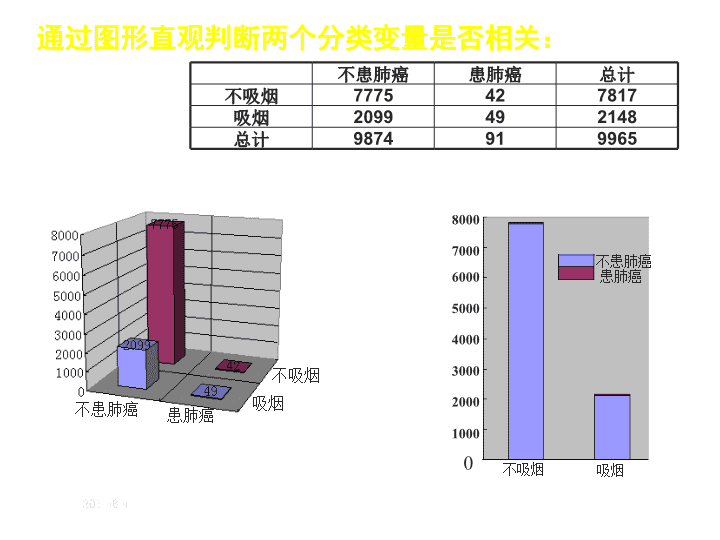
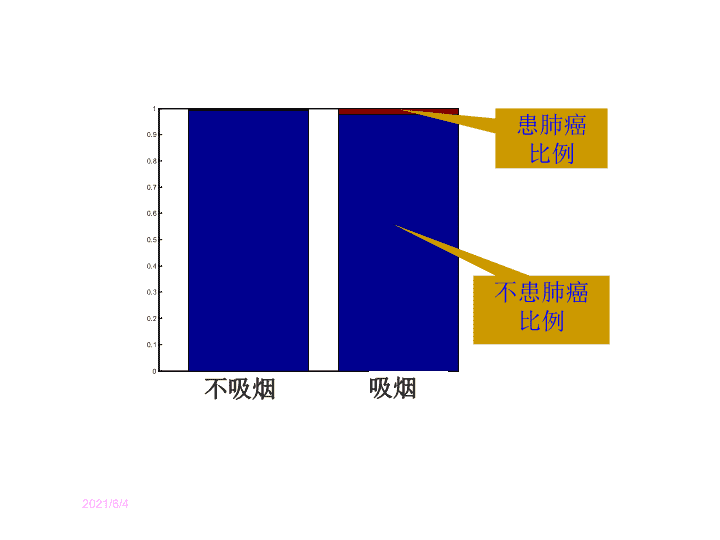
2021/2/15 8.4 独立性检验的基本思想及其初步应用（二） 高二数学 选修 2-3 2021/2/15 不患肺癌 患肺癌 总计 不吸烟 7775 42 7817 吸烟 2099 49 2148 总计 9874 91 9965 1 、列联表 2 、三维柱形图 3 、二维条形图 不患肺癌 患肺癌 吸烟 不吸烟 不患肺癌 患肺癌 吸烟 不吸烟 0 8000 7000 6000 5000 4000 3000 2000 1000 从三维柱形图能清晰看出 各个频数的相对大小。 从二维条形图能看出，吸烟者中 患肺癌的比例高于不患肺癌的比例。 通过图形直观判断两个分类变量是否相关： 2021/2/15 不吸烟 吸烟 患肺癌 比例 不患肺癌 比例 4 、等高条形图 等高条形图更清晰地表达了两种情况下患肺癌的比例。 2021/2/15 随机变量 ----- 卡方统计量 5 、 独立性检验 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828 临界值表 0.1% 把握认为 A 与 B 无关 1% 把握认为 A 与 B 无关 99.9% 把握认 A 与 B 有关 99% 把握认为 A 与 B 有关 90% 把握认为 A 与 B 有关 10% 把握认为 A 与 B 无关 没有充分的依据显示 A 与 B 有关，但也不能显示 A 与 B 无关 2021/2/15 第一步： H 0 ： 吸烟 和 患病 之间没有关系 患病 不患病 总计 吸烟 a b a+b 不吸烟 c d c+d 总计 a+c b+d a+b+c+d 第二步：列出 2 ×2 列联表 6 、独立性检验的步骤 第三步：计算 第四步：查对临界值表，作出判断。 P( k ≥k 0 ) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001 k 0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828 2021/2/15 反证法原理与假设检验原理 反证法原理： 在一个已知假设下，如果 推出一个矛盾 ，就 证明 了这个假设不成立。 假设检验原理： 在一个已知假设下，如果 一个与该假设矛盾的小概率事件发生 ， 就 推断 这个假设不成立。 2021/2/15 例 1 在某医院，因为患心脏病而住院的 665 名男性病人中，有 214 人秃顶；而另外 772 名不是因为患心脏病而住院的男性病人中有 175 人秃顶。分别利用图形和独立性检验方法判断秃顶与患心脏病是否有关系？你所得的结论在什么范围内有效？ 解：根据题目所给数据得到如下列联表： 患心脏病 不患心脏病 总计 秃顶 214 175 389 不秃顶 451 597 1048 总计 665 772 1437 相应的三维柱形图如图所示，比较来说，底面副对角线上两个柱体高度的乘积要大一些，因此可以在某种程度上认为“秃顶与患心脏病有关”。 秃头 不秃头 2021/2/15 例 1 在某医院，因为患心脏病而住院的 665 名男性病人中，有 214 人秃顶；而另外 772 名不是因为患心脏病而住院的男性病人中有 175 人秃顶。分别利用图形和独立性检验方法判断秃顶与患心脏病是否有关系？你所得的结论在什么范围内有效？ 解：根据题目所给数据得到如下列联表： 患心脏病 不患心脏病 总计 秃顶 214 175 389 不秃顶 451 597 1048 总计 665 772 1437 根据联表 1-13 中的数据，得到 所以有 99% 的把握认为“秃顶患心脏病有关”。 2021/2/15 例 1. 秃头与患心脏病 在解决实际问题时，可以 直接计算 K 2 的观测值 k 进行独立检验，而 不必写出 K 2 的推导过程 。 本例中的边框中的注解，主要是使得学生们注意统计结果的适用范围（这由样本的代表性所决定）。 因为这组数据来自住院的病人，因此所得到的结论 适合住院的病人群体． 2021/2/15 例 2 为考察高中生的性别与是否喜欢数学课程之间的关系，在某城市的某校高中生中随机抽取 300 名学生，得到如下联表： 喜欢数学课程 不喜欢数学课程 总计 男 37 85 122 女 35 143 178 总计 72 228 300 由表中数据计算 K 2 的观测值 k 4.514 。能够以 95% 的把握认为高中生的性别与是否喜欢数学课程之间有关系吗？请详细阐述得出结论的依据。 解：可以有 95% 以上的把握认为“性别与喜欢数学课程之间有关系”。 分别用 a,b,c,d 表示样本中喜欢数学课的男生人数、不喜欢数学课的男生人数、喜欢数学课的女生人数、不喜欢数学课的女生人数。 如果性别与是否喜欢数学课有关系，则男生中喜欢数学课的比例 与女生中喜欢数学课的比例 应该 相差很多 ，即 2021/2/15 例 2 为考察高中生的性别与是否喜欢数学课程之间的关系，在某城市的某校高中生中随机抽取 300 名学生，得到如下联表： 喜欢数学课程 不喜欢数学课程 总计 男 37 85 122 女 35 143 178 总计 72 228 300 由表中数据计算 K 2 的观测值 k 4.514 。能够以 95% 的把握认为高中生的性别与是否喜欢数学课程之间有关系吗？请详细阐述得出结论的依据。 因此， 越大 ， “性别与喜欢数学课程之间 有关系 ”成立的 可能性就越大 。 另一方面，在假设“性别与喜欢数学课程之间 无关系 ”的前提下，事件 的概率为 因此事件 A 是一个 小概率事件 。而由样本数据计算得 的观测值 k=4.514, 即小概率事件 A 发生。因此应该断定“性别与喜欢数学课程之间有关系”成立，并且这种判断结果 出错的可能性约为 5% 。所以，约有 95% 的把握认为“性别与喜欢数学课程之间有关系”。 2021/2/15 例 3. 在 500 人身上试验某种血清预防感冒作用，把他们一年中的感冒记录与另外 500 名未用血清的人的感冒记录作比较，结果如表所示。 未感冒 感冒 合计 使用血清 252 248 500 未使用血清 224 276 500 合计 476 524 1000 试画出列联表的条形图，并通过图形判断这种血清能否起到预防感冒的作用？并进行独立性检验。 解：设 H 0 ：感冒与是否使用该血清没有关系。 因当 H 0 成立时， K 2 ≥6.635 的概率约为 0.01 ，故有 99% 的把握认为该血清能起到预防感冒的作用。 P(k≥k 0 ) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001 k 0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828 2021/2/15 P(k≥k 0 ) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001 k 0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828 有效 无效 合计 口服 58 40 98 注射 64 31 95 合计 122 71 193 解：设 H 0 ：药的效果与给药方式没有关系。 因当 H 0 成立时， K 2 ≥1.3896 的概率大于 15% ，故不能否定假设 H 0 ，即不能作出药的效果与给药方式有关的结论。 例 4 ：为研究不同的给药方式（口服与注射）和药的效果（有效与无效）是否有关，进行了相应的抽样调查，调查的结果列在表中，根据所选择的 193 个病人的数据，能否作出药的效果和给药方式有关的结论？ 2021/2/15 P(k≥k 0 ) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001 k 0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828 例 5 ：气管炎是一种常见的呼吸道疾病，医药研究人员对两种中草药治疗慢性气管炎的疗效进行对比，所得数据如表所示，问：它们的疗效有无差异？ 有效 无效 合计 复方江剪刀草 184 61 245 胆黄片 91 9 100 合计 275 70 345 解：设 H 0 ：两种中草药的治疗效果没有差异。 因当 H 0 成立时， K 2 ≥10.828 的概率为 0.001 ，故有 99.9% 的把握认为，两种药物的疗效有差异。 2021/2/15 高考真题 2010 年辽宁卷 2021/2/15 2021/2/15 2021/2/15