2014年高考试题——数学理（山东卷）原卷版

2014年高考试题——数学理（山东卷）原卷版

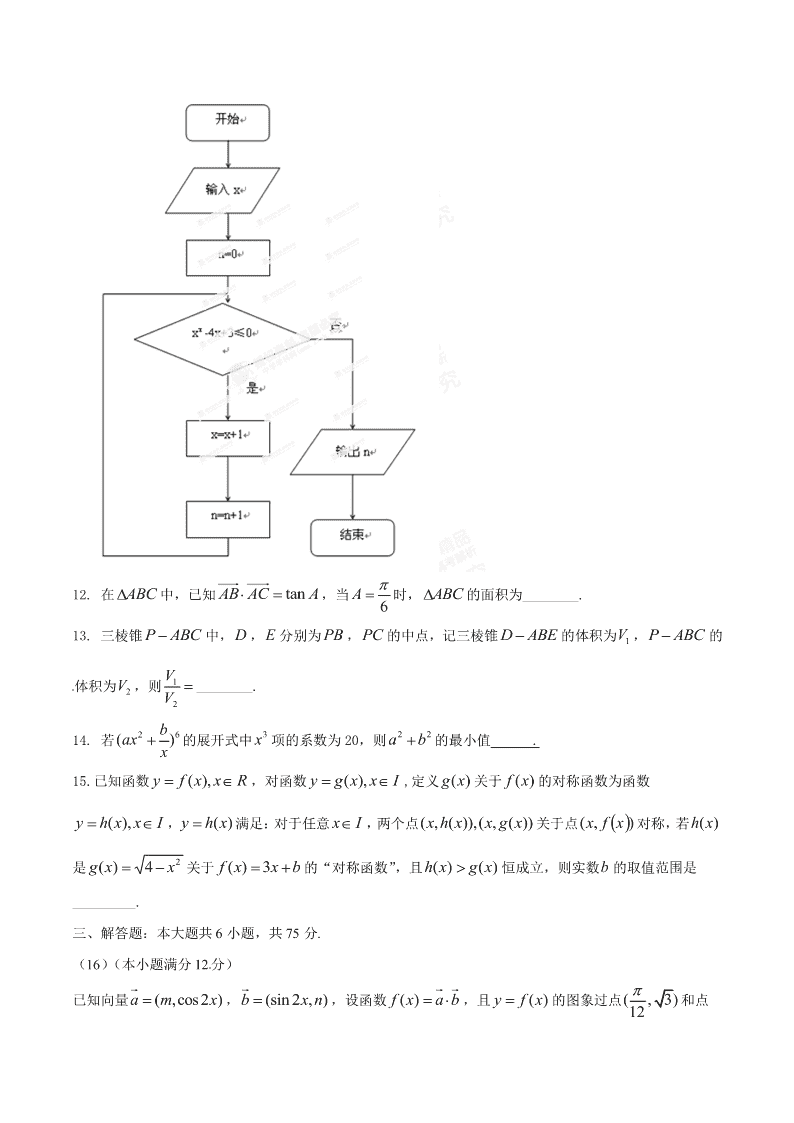
一、选择题 1. 已知 Rba , ，i 是虚数单位，若 ia  与 bi2 互为共轭复数，则  2)( bia （ ） A. i45 B. i45 C. i43 D. i43 2. 设集合    ]2,0[,2|,2|1||  xyyBxxA x ，则 BA （ ） A. ]2,0[ B. )3,1( C. )3,1[ D. )4,1( [来源:Z*xx*k.Com] 3. 函数 1)(log 1)( 2 2   x xf 的定义域为（ ） A. )2 1,0( B. ),2(  C. ),2()2 1,0(  D. ),2[]2 1,0(  4. 用反证法证明命题“设 ba, 为实数，则方程 02  baxx 至少有一个实根”时，要做的假设是（ ） A.方程 没有实根 B.方程 至多有一个实根 C.方程 至多有两个实根 D.方程 恰好有两个实根 5. 已知实数 yx, 满足 )10(  aaa yx ，则下面关系是恒成立的是（ ） A. 1 1 1 1 22  yx B. )1ln()1(ln 22  yx C. yx sinsin  D. 33 yx  6. 直线 34 xyxy  与曲线 在第一象限内围成的封闭图形的面积为（ ） A. 22 B. 24 C. 2 D.4 7. 为了研究某药品的疗效，选取若干名志愿者进行临床试验，所有志愿者的舒张压数据（单位：kPa）的 分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组，第二 组，  ，第五组，右图是根据试验数据制成的频 率分布直方图，已知第一组与第二组共有 20 人，第三 组中没有疗效的有 6 人，则第三组中有疗效的人数为（ ） A.6 B.8 C.12 D.18 8. 已知函数 ( ) 2 1, ( ) .f x x g x kx    若方程 ( ) ( )f x g x 有两个不相等的实根，则实数k 的取值范围 是（ ） A. 1(0, )2 B. 1( ,1)2 C.(1,2) D.(2, ) 9. 已知 ,xy满足约束条件 10 2 3 0 xy xy        ，当目标函数 ( 0, 0)z ax by a b    在该约束条件下取到最小 值 25时， 22ab 的最小值为（ ） A.5 B.4 C. 5 D.2 10. 已知 0 ba ，椭圆 1C 的方程为 12 2 2 2  b y a x ，双曲线 2C 的方程为 22 221xy ab， 与 的离心率之 积为 2 3 ，则 的渐近线方程为（ ） A. 02  yx B. 02  yx C. 02  yx D. 02  yx 二、填空题 11. 执行右面的程序框图，若输入的 x 的值为 1，则输出的 n 的值为________. 12. 在 ABC 中，已知 tanAB AC A ，当 6A  时， 的面积为________. 13. 三棱锥 P ABC 中， D ， E 分别为 PB ， PC 的中点，记三棱锥 D ABE 的体积为 1V ， 的 体积为 2V ，则 1 2 V V  ________. 14. 若 26()bax x 的展开式中 3x 项的系数为 20，则 22 ba  的最小值 . 15.已知函数 Rxxfy  ),( ，对函数 Ixxgy  ),( ,定义 )(xg 关于 )(xf 的对称函数为函数 Ixxhy  ),( ， )(xhy  满足：对于任意 Ix ，两个点 ))(,()),(,( xgxxhx 关于点  ),( xfx 对称，若 )(xh 是 24)( xxg  关于 bxxf  3)( 的“对称函数”，且 )()( xgxh  恒成立，则实数b 的取值范围是 _________. 三、解答题：本大题共 6 小题，共 75 分. （16）（本小题满分 12分） 已知向量 ( ,cos2 )a m x ， (sin 2 , )b x n ，设函数 ()f x a b，且 ()y f x 的图象过点( , 3)12  和点 2( , 2)3   .[来源:Z|xx|k.Com] （Ⅰ）求 ,mn的值；[来源:学科网 ZXXK] （Ⅱ）将 ()y f x 的图象向左平移 （0 ）个单位后得到函数 ()y g x 的图象.若 的图象 上各最高点到点(0,3)的距离的最小值为 1，求 的单调增区间. （17）（本小题满分 12 分） 如图，在四棱柱 1 1 1 1ABCD A B C D 中，底面 ABCD是等腰梯形， 60DAB， 22AB CD， M 是 线段 AB 的中点. （Ⅰ）求证： 1 1 1//C M A ADD ；[来源:Z§xx§k.Com] （Ⅱ）若 1CD 垂直于平面 且 1 3CD  ，求平面 11C D M 和平面 所成的角（锐角）的余弦值.[来 源:学科网] （18）（本小题满分12 分） 乒乓球台面被球网分成甲、乙两部分，如图， 甲上有两个不相交的区域 ,AB，乙被划分为两个不相交的区域 ,CD.某次测试要求队员接到落点在甲上的来球后向乙回球.规定：回 球一次，落点在C 上记 3 分，在 D 上记 1 分，其它情况记 0 分.对落点在 A 上的来球，队员小明回球的落点 在C 上的概率为 1 2 ，在 D 上的概率为 1 3 ；对落点在 B 上的来球，小明回球的落点在 上的概率为 1 5 ，在 上的概率为 3 5 .假设共有两次来球且落在 ,AB上各一次，小明的两次回球互不影响.求： （Ⅰ）小明的两次回球的落点中恰有一次的落点在乙上的概率； （Ⅱ）两次回球结束后，小明得分之和 的分布列与数学期望. （19）（本小题满分 12 分） 已知等差数列{}na 的公差为 2，前 n 项和为 nS ，且 1 2 4,,S S S 成等比数列. （Ⅰ）求数列 的通项公式； （Ⅱ）令 1 1 4( 1)n n nn nb aa    ，求数列{}nb 的前 n 项和 nT . （20）（本小题满分 13 分） 设函数 2 2( ) ( ln ) xef x k xxx   （ k 为常数， 2.71828e   是自然对数的底数）. （Ⅰ）当 0k  时，求函数 ()fx的单调区间； （Ⅱ）若函数 ()fx在 (0,2) 内存在两个极值点，求 k 的取值范围.