2014年高考真题——理科数学（四川卷）原卷版

2014年高考真题——理科数学（四川卷）原卷版

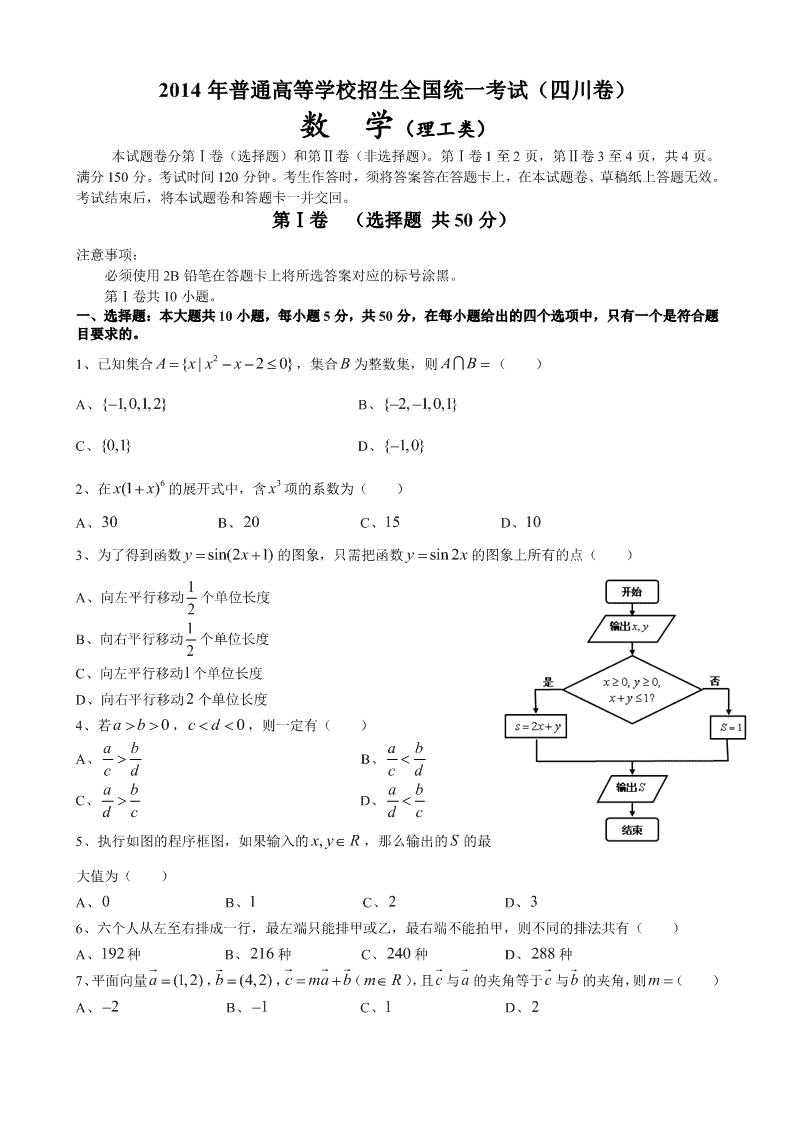
2014 年普通高等学校招生全国统一考试（四川卷） 数 学（理工类） 本试题卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）。第Ⅰ卷 1 至 2 页，第Ⅱ卷 3 至 4 页，共 4 页。 满分 150 分。考试时间 120 分钟。考生作答时，须将答案答在答题卡上，在本试题卷、草稿纸上答题无效。 考试结束后，将本试题卷和答题卡一并交回。 第Ⅰ卷 （选择题 共 50 分） 注意事项： 必须使用 2B 铅笔在答题卡上将所选答案对应的标号涂黑。 第Ⅰ卷共 10 小题。 一、选择题：本大题共 10 小题，每小题 5 分，共 50 分，在每小题给出的四个选项中，只有一个是符合题 目要求的。 1、已知集合 2{ | 2 0}A x x x    ，集合 B 为整数集，则 AB （ ） A、{ 1,0,1,2} B、{ 2, 1,0,1} C、{0,1} D、{ 1,0} 2、在 6(1 )xx 的展开式中，含 3x 项的系数为（ ） A、30 B、 20 C、15 D、10 3、为了得到函数 sin(2 1)yx的图象，只需把函数 sin 2yx 的图象上所有的点（ ） A、向左平行移动 1 2 个单位长度 B、向右平行移动 1 2 个单位长度 C、向左平行移动1个单位长度 D、向右平行移动 2 个单位长度 4、若 0ab， 0cd，则一定有（ ） A、 ab cd B、 ab cd C、 ab dc D、 ab dc 5、执行如图的程序框图，如果输入的 ,x y R ，那么输出的 S 的最 大值为（ ） A、0 B、1 C、 2 D、3 6、六个人从左至右排成一行，最左端只能排甲或乙，最右端不能拍甲，则不同的排法共有（ ） A、192种 B、 216 种 C、 240 种 D、 288 种 7、平面向量 (1,2)a  ， (4,2)b  ，c ma b（ mR ），且 c 与 a 的夹角等于c 与b 的夹角，则 m （ ） A、 2 B、 1 C、1 D、 2 8、如图，在正方体 1 1 1 1ABCD A B C D 中，点O 为线段 BD 的中点。设点 P 在线段 1CC 上，直线OP 与平面 1A BD 所成的角为 ，则sin 的取值范围 是（ ） A、 3[ ,1]3 B、 6[ ,1]3 C、 6 2 2[ , ]33 D、 22[ ,1]3 9、已知 ( ) ln(1 ) ln(1 )f x x x    ， ( 1,1)x 。现有下列命题：① ( ) ( )f x f x   ；② 2 2( ) 2 ( )1 xf f xx  ； ③| ( ) | 2| |f x x 。其中的所有正确命题的序号是（ ） A、①②③ B、②③ C、①③ D、①② 10、已知 F 为抛物线 2yx 的焦点，点 A ，B 在该抛物线上且位于 x 轴的两侧， 2OA OB（其中O 为 坐标原点），则 ABO 与 AFO 面积之和的最小值是（ ） A、 2 B、3 C、17 2 8 D、 10 第Ⅱ卷 （非选择题 共 100 分） 注意事项： 必须使用 0.5 毫米黑色墨迹签字笔在答题卡上题目所示的答题区域内作答。作图题可先用铅笔绘出， 确认后再用 0.5 毫米黑色墨迹签字笔描清楚。答在试题卷、草稿纸上无效。 第Ⅱ卷共 11 小题。 二、填空题：本大题共 5 小题，每小题 5 分，共 25 分。 11、复数 22 1 i i   ____________。 12、设 ()fx是定义在 R 上的周期为 2 的函数，当 [ 1,1)x 时， 24 2, 1 0,() , 0 1, xxfx xx        ，则 3()2f  ____________。 13、如图，从气球 A 上测得正前方的河流的两岸 B ，C 的俯角分别为67 ，30 ， 此时气球的高是 46cm ，则河流的宽度 BC 约等于____________ m 。（用四舍五入 法将结果精确到个位。参考数据：sin67 0.92 ，cos67 0.39 ，sin37 0.60 ， cos37 0.80 ， 3 1.73 ） 14、设 mR ，过定点 A 的动直线 0x my和过定点 B 的动直线 30mx y m    交于点 ( , )P x y ，则 | | | |PA PB 的最大值是____________ O B1A1 C1D1 B D C A P 67° 30° 46m B C A 15、以 A 表示值域为 R 的函数组成的集合，B 表示具有如下性质的函数 ()x 组成的集合：对于函数 ， 存在一个正数 M ，使得函数 的值域包含于区间[ , ]MM 。例如，当 3 1()xx  ， 2 ( ) sinxx  时， 1()xA  ， 2 ()xB  。现有如下命题： ①设函数 ()fx的定义域为 D ，则“ ()f x A ”的充要条件是“ bR ， aD ， ()f a b ”； ②若函数 ()f x B 的充要条件是 ()fx有最大值和最小值； ③若函数 ()fx， ()gx的定义域相同，且 ()f x A ， ()g x B ，则 ( ) ( )f x g x B； ④若函数 2( ) ln( 2) 1 xf x a x x    （ 2x  ， aR ）有最大值，则 ()f x B 。 其中的真命题有____________。（写出所有真命题的序号）。 三、解答题：本大题共 6 小题，共 75 分。解答应写出文字说明，证明过程或演算步骤。 16、(本小题满分 12 分) 已知函数 ( ) sin(3 )4f x x  （Ⅰ）求 ()fx的单调递增区间； （Ⅱ）若 是第二象限角， 4( ) cos( )cos23 5 4f  ，求cos sin 的值。 17、(本小题满分 12 分) 一款击鼓小游戏的规则如下：每盘游戏都需要击鼓三次，每次击鼓要么出现一次音乐，要么不出现音 乐；每盘游戏击鼓三次后，出现一次音乐获得10分，出现两次音乐获得 20 分，出现三次音乐获得100分， 没有出现音乐则扣除 200 分（即获得 200 分）。设每次击鼓出现音乐的概率为 1 2 ，且各次击鼓出现音乐 相互独立。 （Ⅰ）设每盘游戏获得的分数为 X ，求 X 的分布列； （Ⅱ）玩三盘游戏，至少有一盘出现音乐的概率是多少？ （Ⅲ）玩这款游戏的许多人都发现，若干盘游戏后，与最初的分数相比，分数没有增加反而减少了。请运 用概率统计的相关知识分析分数减少的原因。 18、(本小题满分 12 分) 三棱锥 A BCD 及其侧视图、俯视图如图所示。设 M ，N 分别为线段 AD ， AB 的中点，P 为线段 BC 上的点，且 MN NP 。 （Ⅰ）证明： P 为线段 BC 的中点； （Ⅱ）求二面角 A NP M的余弦值。 侧视图 俯视图 1 1 2 2 2 2 1 1 M N P D B C A 19、(本小题满分 12 分) 设等差数列{}na 的公差为 d ，点( , )nnab在函数 ( ) 2xfx 的图象上（ nN ）。 （Ⅰ）若 1 2a  ，点 87( ,4 )ab在函数 ()fx的图象上，求数列{}na 的前 n 项和 nS ； （Ⅱ）若 1 1a  ，函数 ()fx的图象在点 22( , )ab 处的切线在 x 轴上的截距为 12 ln 2 ，求数列{}n n a b 的前 n 项 和 nT 。 20、(本小题满分 13 分) 已知椭圆C ： 22 221xy ab（ 0ab）的焦距为 4 ，其短轴的两个端点与长轴的一个端点构成正三 角形。 （Ⅰ）求椭圆C 的标准方程； （Ⅱ）设 F 为椭圆C 的左焦点，T 为直线 3x  上任意一点，过 F 作TF 的垂线交椭圆C 与点 P ，Q 。 （ⅰ）证明：OT 平分线段 PQ （其中O 为坐标原点）； （ⅱ）当 || || TF PQ 最小时，求点T 的坐标。 21、(本小题满分 14 分) 已知函数 2( ) 1xf x e ax bx    ，其中 ,a b R ， 2.71828e   为自然对数的底数。 （Ⅰ）设 ()gx是函数 ()fx的导函数，求函数 ()gx在区间[0,1] 上的最小值； （Ⅱ）若 (1) 0f  ，函数 ()fx在区间(0,1) 内有零点，求 a 的取值范围。