2014安徽(理科数学)高考试题
2014·安徽卷(理科数学)
1.[2014·安徽卷] 设i是虚数单位,表示复数z的共轭复数.若z=1+i,则+i·=( )
A.-2 B.-2i
C.2 D.2i
1.C [解析] 因为z=1+i,所以+i·=(-i+1)+i+1=2.
2.[2014·安徽卷] “x<0”是“ln(x+1)<0”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
2.B [解析] ln(x+1)<0⇔0<1+x<1⇔-1
zC或zA=zC>zB或zB=zC>zA,
解得a=-1或a=2.
方法二:画出可行域,如图中阴影部分所示,z=y-ax可变为y=ax+z,令l0:y=ax,则由题意知l0∥AB或l0∥AC,故a=-1或a=2.
6.[2014·安徽卷] 设函数f(x)(x∈R)满足f(x+π)=f(x)+sin x.当0≤x<π时,f(x)=0,则f=( )
A. B.
C.0 D.-
6.A [解析] 由已知可得,f=f+sin=f+sin+sin =f+sin+sin+sin=2sin +sin=sin=.
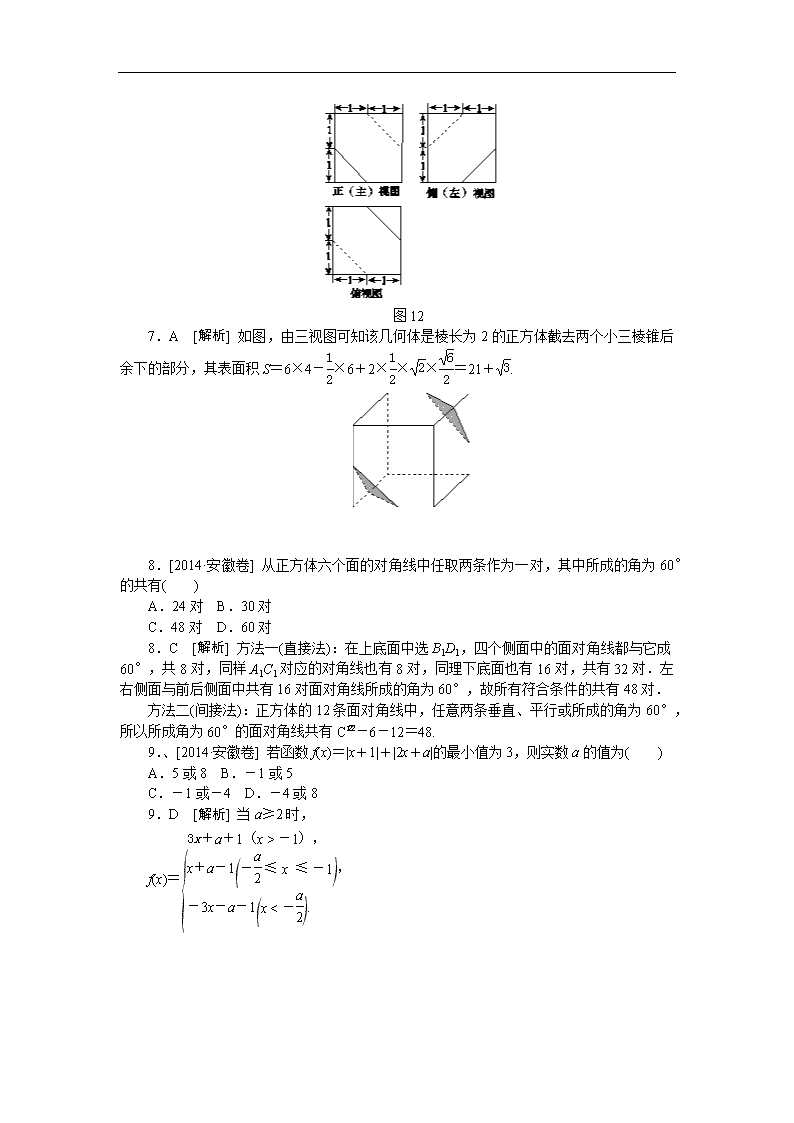
7.[2014·安徽卷] 一个多面体的三视图如图12所示,则该多面体的表面积为( )
A.21+ B.8+
C.21 D.18
图12
7.A [解析] 如图,由三视图可知该几何体是棱长为2的正方体截去两个小三棱锥后余下的部分,其表面积S=6×4-×6+2×××=21+.
8.[2014·安徽卷] 从正方体六个面的对角线中任取两条作为一对,其中所成的角为60°的共有( )
A.24对 B.30对
C.48对 D.60对
8.C [解析] 方法一(直接法):在上底面中选B1D1,四个侧面中的面对角线都与它成60°,共8对,同样A1C1对应的对角线也有8对,同理下底面也有16对,共有32对.左右侧面与前后侧面中共有16对面对角线所成的角为60°,故所有符合条件的共有48对.
方法二(间接法):正方体的12条面对角线中,任意两条垂直、平行或所成的角为60°,所以所成角为60°的面对角线共有C-6-12=48.
9.、[2014·安徽卷] 若函数f(x)=|x+1|+|2x+a|的最小值为3,则实数a的值为( )
A.5或8 B.-1或5
C.-1或-4 D.-4或8
9.D [解析] 当a≥2时,
f(x)=
由图可知,当x=-时,fmin(x)=f=-1=3,可得a=8.
当a<2时,f(x)
由图可知,当x=-时,fmin(x)=f=-+1=3,可得a=-4.综上可知,a的值为-4或8.
10.、[2014·安徽卷] 在平面直角坐标系xOy中,已知向量a,b,|a|=|b|=1,a·b=0,点Q满足=(a+b).曲线C={P|=acos θ+bsin θ,0≤θ<2π},区域Ω={P|0<r≤|PQ|≤R,r<R}.若C∩Ω为两段分离的曲线,则( )
A.1<r<R<3 B.1<r<3≤R
C.r≤1<R<3 D.1<r<3<R
10.A [解析]由已知可设=a=(1,0),=b=(0,1),P(x,y),则=(,),|OQ|=2.
曲线C={P|=(cos θ,sin θ),0≤θ<2π},
即C:x2+y2=1.
区域Ω={P|00时,φmin=.
方法二:由f(x)=sin的图像向右平移φ个单位后所得的图像关于y轴对称可知,-2φ=+kπ,k∈Z,又φ>0,所以φmin=.
12.、[2014·安徽卷] 数列{an}是等差数列,若a1+1,a3+3,a5+5构成公比为q的等比数列,则q=________.
12.1 [解析] 因为数列{an}是等差数列,所以a1+1,a3+3,a5+5也成等差数列.又 a1+1,a3+3,a5+5构为公比为q的等比数列,所以a1+1,a3+3,a5+5为常数列,故q=1.
13.[2014·安徽卷] 设a≠0,n是大于1的自然数,的展开式为a0+a1x+a2x2+…+anxn.若点Ai(i,ai)(i=0,1,2)的位置如图13所示,则a=________.
图13
13.3 [解析] 由图可知a0=1,a1=3,a2=4,由组合原理知故
eq �lc{(avs4alco1(f(n,a)=3,,f(n(n-1),a2)=8,))
解得
14.[2014·安徽卷] 设F1,F2分别是椭圆E:x2+=1(0<b<1)的左、右焦点,过点F1的直线交椭圆E于A,B两点.若|AF1|=3|F1B|,AF2⊥x轴,则椭圆E的方程为________.
14.x2+y2=1 [解析]
设F1(-c,0),F2(c,0),其中c=,
则可设A(c,b2),B(x0,y0),由|AF1|=3|F1B|,
可得=3,故即代入椭圆方程可得+b2=1,解得b2=,故椭圆方程为x2+=1.
15.[2014·安徽卷] 已知两个不相等的非零向量a,b,两组向量,,,,和,,,,均由2个a和3个b排列而成.记S=x1·y1+x2·y2+x3·y3+x4·y4+x5·y5,Smin表示S所有可能取值中的最小值,则下列命题正确的是________(写出所有正确命题的编号).
①S有5个不同的值
②若a⊥b,则Smin与|a|无关
③若a∥b,则Smin与|b|无关
④若|b|>4|a|,则Smin>0
⑤若|b|=2|a|,Smin=8|a|2,则a与b的夹角为
15.②④ [解析] S可能的取值有3种情况:S1=2+3,=+2+2a·b,S3=+4a·b,所以S最多只有3个不同的值.
因为a,b是不相等的向量,所以S1-S3=2+2-4a·b=2(a-b)>0,S1-S2=+-2a·b=(a-b)2>0,S2-S3=(a-b)>0,所以S3||-4|a||b|>16|a|2-|a|2=0,所以Smin>0,故④正确;
对于⑤,|b|=2|a|,Smin=4|a|2+8|a|2cos θ=8|a|2,所以cos θ=,又θ∈[0,π],所以θ=,故⑤错误.
16.、[2014·安徽卷] 设△ABC的内角A,B,C所对边的长分别是a,b,c,且b=3,c=1,A=2B.
(1)求a的值;
(2)求sin的值.
16.解: (1)因为A=2B,所以sin A=sin 2B=2sin Bcos B,由余弦定理得cos B==,所以由正弦定理可得a=2b·.
因为b=3,c=1,所以a2=12,即a=2 .
(2)由余弦定理得cos A===
-.因为0x2时,f′(x)<0;
当x10.
故f(x)在和 内单调递减,
在内单调递增.
(2)因为a>0,所以x1<0,x2>0,
①当a≥4时,x2≥1.
由(1)知,f(x)在[0,1]上单调递增,
所以f(x)在x=0和x=1处分别取得最小值和最大值.
②当01+2x,原不等式成立.
②假设p=k(k≥2,k∈N*)时,不等式(1+x)k>1+kx成立.
当p=k+1时,(1+x)k+1=(1+x)(1+x)k>(1+x)(1+kx)=1+(k+1)x+kx2>1+(k+1)x.
所以当p=k+1时,原不等式也成立.
综合①②可得,当x>-1,x≠0时,对一切整数p>1,不等式(1+x)p>1+px均成立.
(2)方法一:先用数学归纳法证明an>c.
①当n=1时,由题设知a1>c成立.
②假设n=k(k≥1,k∈N*)时,不等式ak>c成立.
由an+1=an+a易知an>0,n∈N*.
当n=k+1时,=+a=
1+.
由ak>c>0得-1<-<<0.
由(1)中的结论得=>1+p· =.
因此a>c,即ak+1>c,
所以当n=k+1时,不等式an>c也成立.
综合①②可得,对一切正整数n,不等式an>c均成立.
再由=1+可得<1,
即an+1an+1>c,n∈N*.
方法二:设f(x)=x+x1-p,x≥c,则xp≥c,
所以f′(x)=+(1-p)x-p=>0.
由此可得,f(x)在[c,+∞)上单调递增,因而,当x>c时,f(x)>f(c)=c.
①当n=1时,由a1>c>0,即a>c可知
a2=a1+a=a1c,从而可得a1>a2>c,
故当n=1时,不等式an>an+1>c成立.
②假设n=k(k≥1,k∈N*)时,不等式ak>ak+1>c成立,则当n=k+1时,f(ak)>f(ak+1)>f(c),
即有ak+1>ak+2>c,
所以当n=k+1时,原不等式也成立.
综合①②可得,对一切正整数n,不等式an>an+1>c均成立.