高考数学复习专题练习第8讲 曲线与方程

高考数学复习专题练习第8讲 曲线与方程

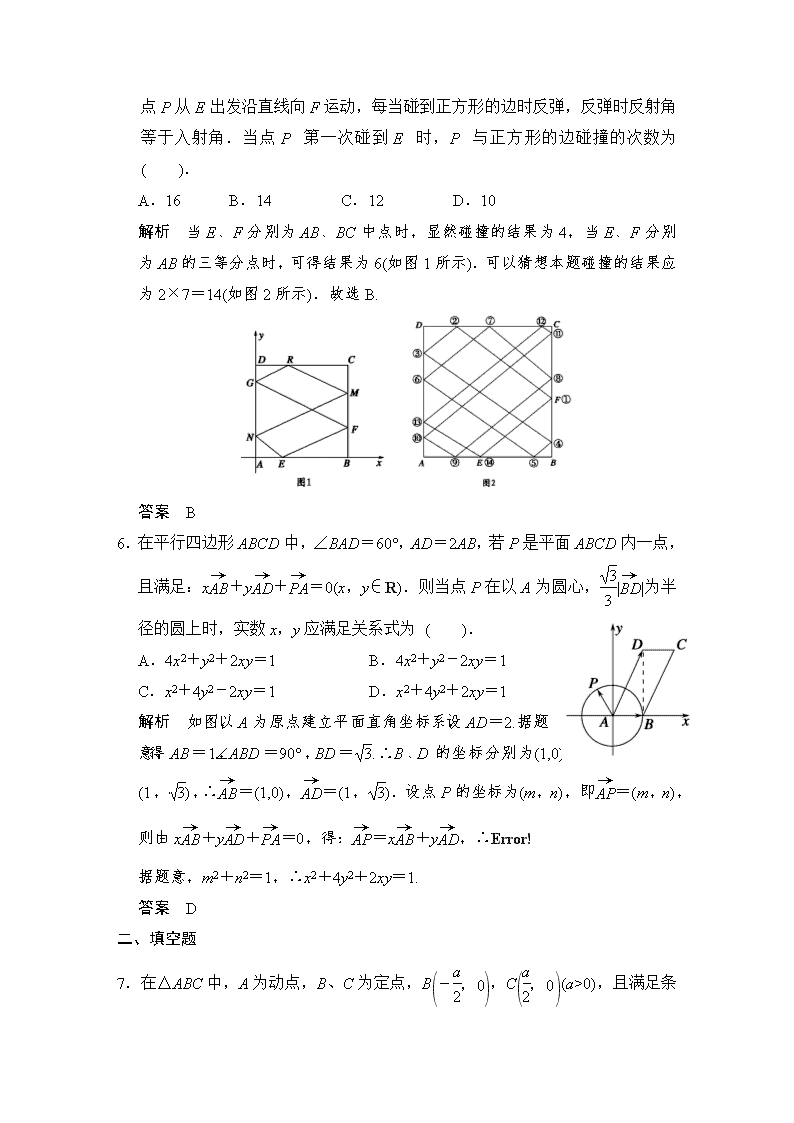
第8讲 曲线与方程 一、选择题 ‎1．若点P到直线x＝－1的距离比它到点(2,0)的距离小1，则点P的轨迹为(　　)．‎ A．圆 B．椭圆 C．双曲线 D．抛物线 解析　依题意，点P到直线x＝－2的距离等于它到点(2,0)的距离，故点P的轨迹是抛物线．‎ 答案　D ‎2． 动点P(x，y)满足5＝|3x＋4y－11|，则点P的轨迹是 (　　)．‎ A．椭圆 B．双曲线 C．抛物线 D．直线 解析　设定点F(1,2)，定直线l：3x＋4y－11＝0，则|PF|＝，点P到直线l的距离d＝.‎ 由已知得＝1，但注意到点F(1,2)恰在直线l上，所以点P的轨迹是直线．选D.‎ ‎ 答案　D ‎3．设圆(x＋1)2＋y2＝25的圆心为C，A(1,0)是圆内一定点，Q为圆周上任一点．线段AQ的垂直平分线与CQ的连线交于点M，则M的轨迹方程为 (　　)．‎ A.－＝1 B.＋＝1‎ C.－＝1 D.＋＝1‎ 解析　M为AQ垂直平分线上一点，则|AM|＝|MQ|，∴|MC|＋|MA|＝|MC|＋|MQ|＝|CQ|＝5，故M的轨迹为椭圆，∴a＝，c＝1，则b2＝a2－c2＝，‎ ‎∴椭圆的标准方程为＋＝1.‎ 答案　D ‎4．在△ABC中，A为动点，B，C为定点，B，C且满足条件 sin C－sin B＝sin A，则动点A的轨迹方程是(　　)‎ A.－＝1(y≠0)‎ B.－＝1(x≠0)‎ C.－＝1(y≠0)的左支 D.－＝1(y≠0)的右支 解析：sin C－sin B＝sin A，由正弦定理得|AB|－|AC|＝|BC|＝a(定值)．‎ ‎∴A点的轨迹是以B，C为焦点的双曲线的右支，其中实半轴长为，焦距为|BC|＝a.‎ ‎∴虚半轴长为＝a，由双曲线标准方程得动点A的轨迹方程为－＝1(y≠0)的右支．‎ 答案：D ‎5．正方形ABCD的边长为1，点E在边AB上，点F在边BC上，AE＝BF＝.动点P从E出发沿直线向F运动，每当碰到正方形的边时反弹，反弹时反射角等于入射角．当点P第一次碰到E时，P与正方形的边碰撞的次数为(　　)．‎ A．16 B．‎14 ‎ C．12 D．10‎ 解析　当E、F分别为AB、BC中点时，显然碰撞的结果为4，当E、F分别为AB的三等分点时，可得结果为6(如图1所示)．可以猜想本题碰撞的结果应为2×7＝14(如图2所示)．故选B.‎ 答案　B ‎6．在平行四边形ABCD中，∠BAD＝60°，AD＝2AB，若P是平面ABCD内一点，且满足：x＋y＋＝0(x，y∈R)．则当点P在以A为圆心，||为半径的圆上时，实数x，y应满足关系式为 (　　)．‎ A．4x2＋y2＋2xy＝1 B．4x2＋y2－2xy＝1‎ C．x2＋4y2－2xy＝1 D．x2＋4y2＋2xy＝1‎ 解析　如图，以A为原点建立平面直角坐标系，设AD＝2.据题意，得AB＝1，∠ABD＝90°，BD＝.∴B、D的坐标分别为(1,0)、(1，)，∴＝(1,0)，＝(1，)．设点P的坐标为(m，n)，即＝(m，n)，则由x＋y＋＝0，得：＝x＋y，∴ 据题意，m2＋n2＝1，∴x2＋4y2＋2xy＝1.‎ 答案　D 二、填空题 ‎7．在△ABC中，A为动点，B、C为定点，B，C(a>0)，且满足条件sin C－sin B＝sin A，则动点A的轨迹方程是________．‎ 解析　由正弦定理，得－＝×，‎ ‎∴|AB|－|AC|＝|BC|，且为双曲线右支．‎ 答案　－＝1(x>0且y≠0)‎ ‎8. 如图，点F(a,0)(a>0)，点P在y轴上运动，M在x 轴上运动，N为动点，且·＝0，＋＝0，则点N的轨迹方程为________．‎ 解析　由题意，知PM⊥PF且P为线段MN的中点，连接FN，延长FP至点Q使P恰为QF之中点；连接QM，QN，则四边形FNQM为菱形，且点Q恒在直线l：x＝－a上，故点N的轨迹是以点F为焦点，直线l为准线的抛物线，其方程为：y2＝4ax.‎ 答案　y2＝4ax ‎9．设定点M(－3,4)，动点N在圆x2＋y2＝4上运动，以OM、ON为邻边，‎ 作平行四边形MONP，则点P的轨迹方程为________．‎ 解析 设P(x，y)，圆上的动点N(x0，y0)，则线段OP的中点坐标为，线段MN的中点坐标为，又因为平行四边形的对角线互相平分，所以有： 可得 又因为N(x0，y0)在圆上，所以N点坐标应满足圆的方程．即有(x＋3)2＋(y－4)2＝4，但应除去两点和.‎ 答案 (x＋3)2＋(y－4)2＝4 ‎10． P是椭圆＋＝1上的任意一点，F1、F2是它的两个焦点，O为坐标原点，＝＋，则动点Q的轨迹方程是________．‎ 解析　由＝＋，又＋＝＝2 ＝－2，设Q(x，y)，则＝－＝－(x，y)＝－，－，即P点坐标为－，－.又P在椭圆上，则有＋＝1，即＋＝1.‎ 答案　＋＝1‎ 三、解答题 ‎11．设椭圆方程为x2＋＝1，过点M(0,1)的直线l交椭圆于A，B两点，O为坐标原点，点P满足＝(＋)，点N的坐标为，当直线l绕点M旋转时，求：‎ ‎(1)动点P的轨迹方程；‎ ‎(2)||的最大值，最小值．‎ 解　(1)直线l过定点M(0,1)，当其斜率存在时设为k，则l的方程为y＝kx＋1.‎ 设A(x1，y1)，B(x2，y2)，由题意知，A、B的坐标满足方程组消去y得(4＋k2)x2＋2kx－3＝0.‎ 则Δ＝4k2＋12(4＋k2)>0.‎ ‎∴x1＋x2＝－，x1x2＝.‎ P(x，y)是AB的中点，‎ 则由 消去k得4x2＋y2－y＝0.‎ 当斜率k不存在时，AB的中点是坐标原点，也满足这个方程，故P点的轨迹方程为4x2＋y2－y＝0.‎ ‎(2)由(1)知4x2＋2＝，∴－≤x≤ 而|NP|2＝2＋2＝2＋ ‎＝－32＋，‎ ‎∴当x＝－时，||取得最大值，‎ 当x＝时，||取得最小值.‎ ‎12．在平面直角坐标系xOy中，椭圆E：＋＝1(a>0，b>0)经过点A，且点F(0，－1)为其一个焦点．‎ ‎(1)求椭圆E的方程；‎ ‎(2)设随圆E与y轴的两个交点为A1，A2，不在y轴上的动点P在直线y＝b2上运动，直线PA1，PA2分别与椭圆E交于点M，N，证明：直线MN通过一个定点，且△FMN的周长为定值．‎ 解　(1)根据题意可得可解得 ‎∴椭圆E的方程为＋＝1.‎ ‎(2)由(1)知A1(0,2)，A2(0，－2)，P(x0，4)为直线y＝4上一点(x0≠0)，M(x1，y1)，N(x2，y2)，直线PA1方程为y＝x＋2，直线PA2方程为y＝x－2，点M(x1，y1)，A1(0,2)的坐标满足方程组可得 点N(x2，y2)，A2(0，－2)的坐标满足方程组可得由于椭圆关于y轴对称，当动点P在直线y＝4上运动时，直线MN通过的定点必在y轴上，当x0＝1时，直线MN的方程为y＋1＝，令x＝0，得y＝1可猜测定点的坐标为(0,1)，并记这个定点为B.则直线BM的斜率kBM＝＝＝，直线BN的斜率kBN＝＝＝，∴kBM＝kBN，即M，B，N三点共线，故直线MN通过一个定点B(0，1)，‎ 又∵F(0，－1)，B(0,1)是椭圆E的焦点，‎ ‎∴△FMN周长为|FM|＋|MB|＋|BN|＋|NF|＝4b＝8，为定值．‎ ‎13．已知向量a＝(x，y)，b＝(1,0)，且(a＋b)⊥(a－b)．‎ ‎(1)求点Q(x，y)的轨迹C的方程；‎ ‎(2)设曲线C与直线y＝kx＋m相交于不同的两点M、N，又点A(0，－1)，当|AM|＝|AN|时，求实数m的取值范围．‎ 解　(1)由题意得a＋b＝(x＋，y)，a－b＝(x－，y)，‎ ‎∵(a＋b)⊥(a－b)，∴(a＋b)·(a－b)＝0，‎ 即(x＋)(x－)＋y·y＝0.‎ 化简得＋y2＝1，∴Q点的轨迹C的方程为＋y2＝1.‎ ‎(2)由得(3k2＋1)x2＋6mkx＋3(m2－1)＝0，‎ 由于直线与椭圆有两个不同的交点，‎ ‎∴Δ>0，即m2<3k2＋1. ①‎ ‎(i)当k≠0时，设弦MN的中点为P(xP，yP)，xM、xN分别为点M、N的横坐标，则xP＝＝－，‎ 从而yP＝kxP＋m＝，kAP＝＝－，‎ 又|AM|＝|AN|，∴AP⊥MN.‎ 则－＝－，即‎2m＝3k2＋1， ②‎ 将②代入①得‎2m>m2，解得00，解得m>，‎ 故所求的m的取值范围是.‎ ‎(ii)当k＝0时，|AM|＝|AN|，‎ ‎∴AP⊥MN，m2<3k2＋1，解得－1

查看更多