辽宁省大连市普兰店区第三十八中学2018-2019高二下学期考试数学（理）试卷

辽宁省大连市普兰店区第三十八中学2018-2019高二下学期考试数学（理）试卷

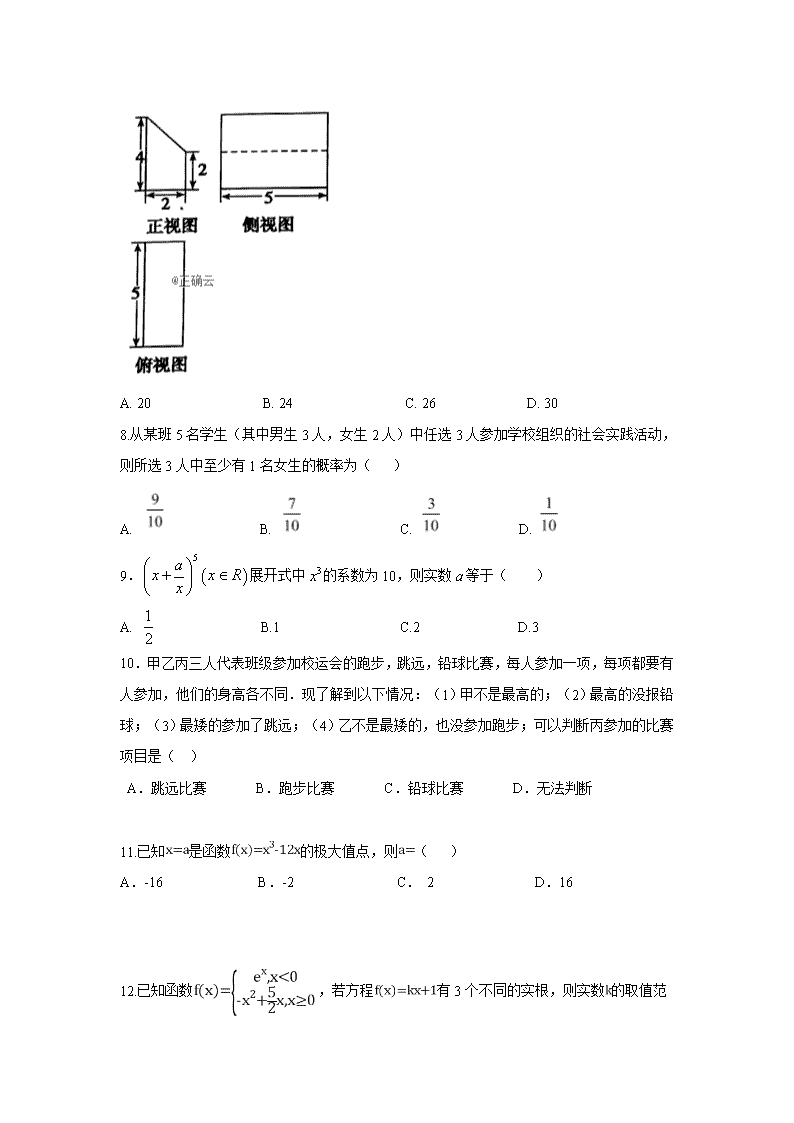
数学（理科）试卷 第Ⅰ卷（客观题 共60分）‎ 一．选择题（本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1.已知集合，，则（ ）‎ ‎ A.{0} B.{0,1} C. {1,2} D.{0,1,2}‎ ‎2.设则的虚部是（ ）‎ A. 3 B．3i C． D．‎ ‎3. 用红、黄两种颜色给图中的A、B、C、D四个小方格涂色，使相邻小方格（有公共边的小格）不同色，则不同的涂色方式种数为( )‎ A. 2 B. 4 C.16 D.84 ‎ ‎4. 已知复数z=m(3+i)-(2+i)在复平面内对应的点在第三象限，则实数m的取值范围是（ ）‎ A． B. C． D. ‎ ‎5.已知双曲线的渐近线方程为3x±5y=0，则此双曲线的离心率为（ ）‎ A. B. C. D. ‎ ‎6.有4个不同的小球放入3个盒子中，每个盒子至少放一个小球，则不同的放法共有（ ）‎ A．12种 B．18种 C．24种 D．36种 ‎7.某几何体的三视图如图所示，则该几何体的体积为（ ）‎ A. 20 B. 24 C. 26 D. 30‎ ‎8.从某班5名学生（其中男生3人，女生2人）中任选3人参加学校组织的社会实践活动，则所选3人中至少有1名女生的概率为（ ）‎ A. B. C. D. ‎ ‎9．展开式中的系数为10，则实数a等于（ ）‎ A. B.1 C.2 D.3 ‎ ‎10．甲乙丙三人代表班级参加校运会的跑步，跳远，铅球比赛，每人参加一项，每项都要有人参加，他们的身高各不同．现了解到以下情况：（1）甲不是最高的；（2）最高的没报铅球；（3）最矮的参加了跳远；（4）乙不是最矮的，也没参加跑步；可以判断丙参加的比赛项目是（ ）‎ A．跳远比赛 B．跑步比赛 C．铅球比赛 D．无法判断 ‎11.已知是函数的极大值点，则（ ）‎ A．-16 B．-2 C． 2 D．16‎ ‎12.已知函数，若方程有3个不同的实根，则实数 的取值范围为（ ）‎ A． B． C． D． ‎ 第Ⅱ卷（主观题 共90分）‎ 二．填空题：（本大题共4小题，每小题5分，共20分）‎ ‎13. 实数满足，则的最小值是 . ‎ ‎14.一批产品的一等品率为，从这批产品中每次随机取一件，有放回地抽取次，表示抽到的一等品件数，则 。‎ ‎15.在的展开式中x3的系数是 ． ‎ ‎16.若函数f(x)=x2 -x+l+alnx在(0，+∞)上单调递增，则实数a的取值范围是 ． ‎ 三．解答题：（本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤）‎ ‎17.（本小题满分10分）[选修4-4:坐标系与参数方程]‎ 在平面直角坐标系中，直线的参数方程为（其中为参数）．以坐标原点为极点，轴正半轴为极轴建立极坐标系并取相同的单位长度，曲线的极坐标方程为．‎ ‎（1）求直线的普通方程和曲线的直角坐标方程；‎ ‎（2）过点作直线的垂线交曲线于，两点，求.‎ ‎18.（本小题满分12分）‎ 在中，角的对边分别为，且 ‎ ‎（1）求；‎ ‎（2）若的面积为，且，求a.‎ ‎19. （本小题满分12分）‎ 如图，在等腰梯形ABCD中，，E，F分别为AB，CD的中点，，M为DF中点。现将四边形BEFC沿EF折起，使平面平面AEFD，得到如图所示的多面体。在图中， (1)证明：； (2)求二面角E-BC-M的余弦值。 ‎ ‎20. （本小题满分12分）‎ 我国2019年新年贺岁大片《流浪地球》自上映以来引发了社会的广泛关注，受到了观众的普遍好评.假设男性观众认为《流浪地球》好看的概率为，女性观众认为《流浪地球》好看的概率为.某机构就《流浪地球》是否好看的问题随机采访了4名观众.‎ ‎（1）若这4名观众2男2女，求这4名观众中女性认为好看的人数比男性认为好看的人数多的概率；‎ ‎（2）若这4名观众都是男性，设X表示这4名观众中认为《流浪地球》好看的人数，求X的分布列与数学期望.‎ ‎21. （本小题满分12分）‎ 在数列中，，且 ‎（1）证明：数列是等差数列；‎ ‎（2）求数列的前n项和。‎ ‎22. （本小题满分12分）‎ 已知函数，，．‎ ‎（1）求函数的极值；‎ ‎（2）若在上为单调函数，求的取值范围；‎ ‎（3）设，若在上至少存在一个，使得成立，求的取值范围．‎ 数学（理科）试卷答案 一、1-12 BCABC DDACB BA ‎ 二、13. - 4 14. 9 15. 1008 16. ‎ 三、17.解:（Ⅰ）直线的参数方程为（其中为参数）消去可得：，‎ 由得，得........5分 ‎（Ⅱ）过点与直线垂直的直线的参数方程为：（为参数），代入可得，设，对应的参数为，，则，所以 ...........10分 ‎18.解： (1)正弦定理，得.‎ ‎(2)‎ 因为,所以 所以 所以 19、 ‎ (1)证明：由题意，在等腰梯形ABCD中，， ，F分别为AB，CD的中点，，，…… 2分 折叠后，，， ，平面DCF， …………4分 又平面DCF，； …………6分 ‎(2)解： …………12分 ‎20. 【解】设表示2名女性观众中认为好看的人数，表示2名男性观众中认为好看的人数，‎ 则，.‎ ‎（1）设事件表示“这4名观众中女性认为好看的人数比男性认为好看的人数多”，,‎ ‎ ‎ ‎（2）X的可能取值为0，1，2，3，4，‎ X服从二项分布 ‎∴X的分布列为 X ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ P ‎∴E(X)= ‎ ‎21.解：（1）的两边同除以，得 ‎，又， ‎ 所以数列是首项为4，公差为2的等差数列。‎ ‎(2)由（1）得，即,‎ 故，‎ 所以 ‎22. 解：：(1)因为.由得，‎ 所以为函数的极小值点 ……4分 ‎（2），.‎ 因为在上为单调函数，所以或 在上恒成立 等价于在恒成立， ． 等价于即在恒成立，而．‎ 综上，的取值范围是． ……… 8分 ‎（3）构造函数，‎ 当时，，所以在不存在使得成立.当时， ‎ 因为，所以在恒成立，‎ 故在单调递增，，‎ 所以只需，解之得，‎ 故的取值范围是 ……… 12分