- 2021-06-24 发布 |
- 37.5 KB |
- 4页
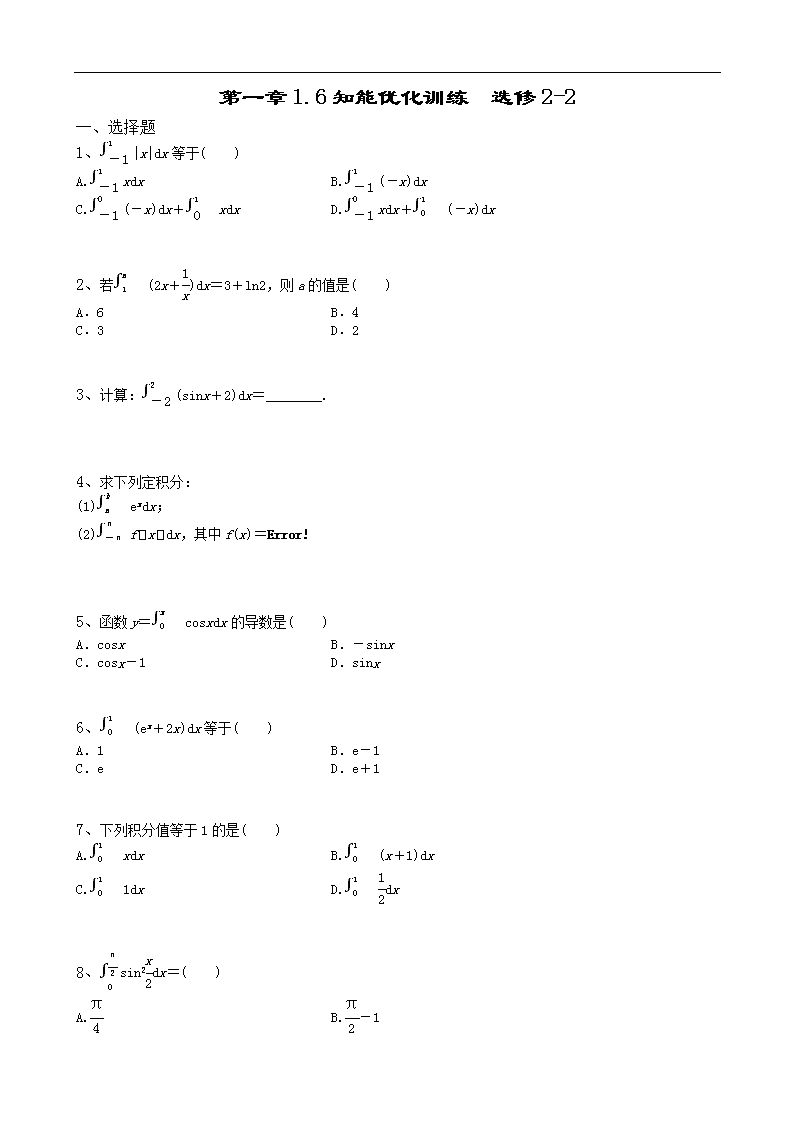


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考数学专题复习:知能优化训练 选修2-2
第一章1.6知能优化训练 选修2-2 一、选择题 1、|x|dx等于( ) A.xdx B.(-x)dx C.(-x)dx+xdx D.xdx+(-x)dx 2、若(2x+)dx=3+ln2,则a的值是( ) A.6 B.4 C.3 D.2 3、计算:(sinx+2)dx=________. 4、求下列定积分: (1)exdx; (2)dx,其中f(x)= 5、函数y=cosxdx的导数是( ) A.cosx B.-sinx C.cosx-1 D.sinx 6、(ex+2x)dx等于( ) A.1 B.e-1 C.e D.e+1 7、下列积分值等于1的是( ) A.xdx B.(x+1)dx C.1dx D.dx 8、sin2dx=( ) A. B.-1 C.2 D. 9、设f(x)是一次函数,且f(x)dx=5,xf(x)dx=,则f(x)的解析式为( ) A.4x+3 B.3x+4 C.-4x+2 D.-3x+4 10、已知f(x)=则f(x)dx的值为( ) A. B. C. D.- 二、填空题 11、由直线x=1,x=4,y=0和曲线y=+1围成的曲边梯形的面积是________. 12、如果f(x)dx=1,f(x)dx=-1,则f(x)dx=________. 13、设函数f(x)=ax2+c(a≠0),若f(x)dx=f(x0),0≤x0≤1,则x0的值为________. 三、解答题 14、求下列定积分. (1)y2(y-2)dy;(2)∫cos2xdx. 15、已知函数f(x)=3x2+2x+1,若f(x)dx=2f(a)成立,求a的值. 16、先作出函数f(x)=的图象,再求f(x)dx. 以下是答案 一、选择题 1、解析:选C.∵|x|= ∴|x|dx=(-x)dx+xdx,故选C. 2、解析:选D.(2x+)dx=2xdx+dx=x2|+lnx|=a2-1+lna=3+ln2,解得a=2. 3、8 解析:(sinx+2)dx=(-cosx+2x)|=-cos2+4-(-cos2-4)=8. 4、解:(1)∵(ex)′=ex, ∴exdx=ex|=eb-ea. (2)dx=cosxdx+sinxdx =sinx|+(-cosx)|=2. 5、解析:选A.y=cosxdx=sinx|=sinx, ∴y′=(sinx)′=cosx,故选A. 6、解析:选C.(ex+2x)dx=(ex+x2)|=(e1+12)-(e0+02)=e. 7、解析:选C.1dx=x|=1,故选C. 8、解析:选D. sin2dxdx=(x-sinx)|=,故选D. 9、解析:选A.∵f(x)是一次函数,设f(x)=ax+b(a≠0),则f(x)dx=(ax+b)dx=axdx+bdx=a+b=5,xf(x)dx=x(ax+b)dx=(ax2)dx+bxdx=a+b=. 由解得a=4,b=3,故f(x)=4x+3. 10、解析:选B.f(x)dx=x2dx+1dx=|+1=+1=,故选B. 二、填空题 11、 解析:设所求面积为S,由定积分的几何意义知 S=(+1)dx=(x+x)| =(+4)-(+1)=. 12、-2 解析:∵f(x)dx=f(x)dx+f(x)dx, ∴1+f(x)dx=-1,∴f(x)dx=-2. 13、 解析:f(x)dx=(ax2+c)dx =(ax3+cx)|=+c=ax+c. 又∵0≤x0≤1,∴x0=. 三、解答题 14、解:(1)y2(y-2)dy=(y3-2y2)dy =(y4-y3)|=. (2)F(x)=sin2x, 则cos2xdx=F()-F()=(2-). 15、解:因为(x3+x2+x)′=3x2+2x+1, 所以 (3x2+2x+1)dx=(x3+x2+x)|=4, 所以2(3a2+2a+1)=4, 即3a2+2a-1=0,解得a=-1或a=. 16、解: 图象如图所示,f(x)dx=x2dx+xdx+3dx=x3|+x2|+3x| =+4+6=10.查看更多