专题35 一元二次不等式及其解法-2020年领军高考数学一轮复习(文理通用) Word版含解析
专题35一元二次不等式及其解法
最新考纲
1.会从实际问题的情境中抽象出一元二次不等式模型.
2.通过函数图象了解一元二次不等式与相应的二次函数、一元二次方程的联系.
3.会解一元二次不等式,对给定的一元二次不等式,会设计求解的程序框图.
基础知识融会贯通
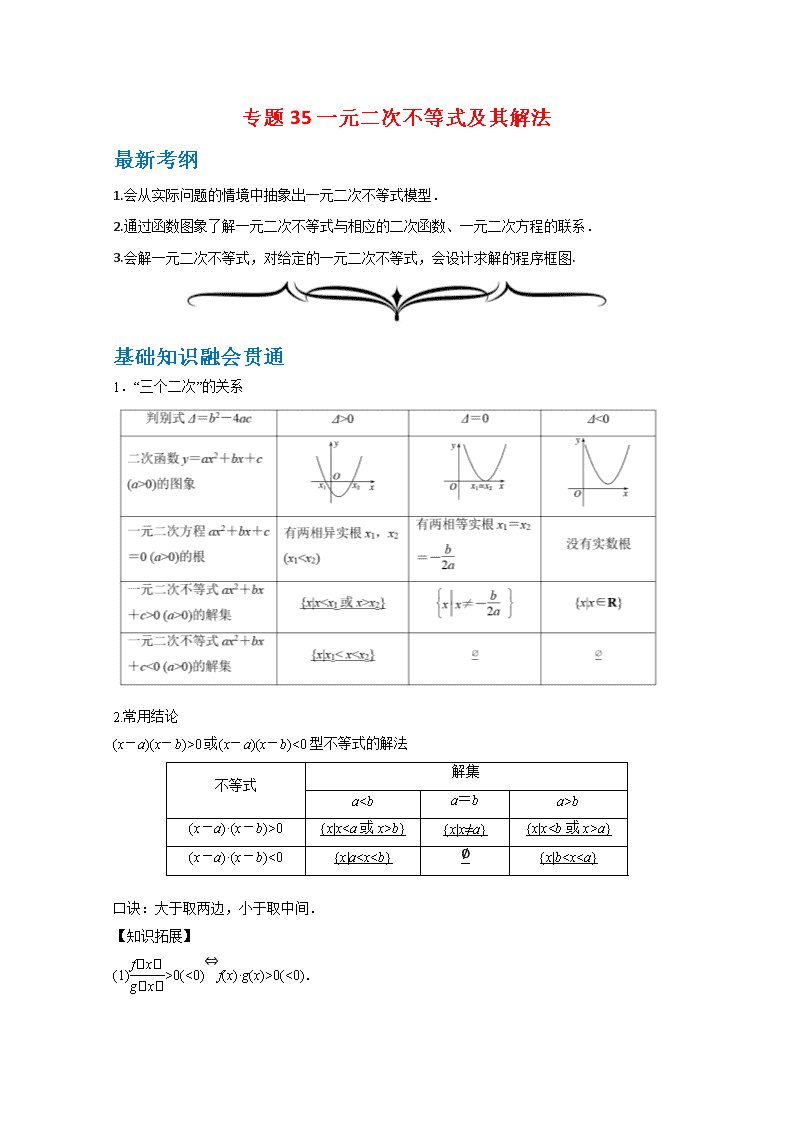
1.“三个二次”的关系
2.常用结论
(x-a)(x-b)>0或(x-a)(x-b)<0型不等式的解法
不等式
解集
a
b
(x-a)·(x-b)>0
{x|xb}
{x|x≠a}
{x|xa}
(x-a)·(x-b)<0
{x|a0(<0)⇔f(x)·g(x)>0(<0).
(2)≥0(≤0)⇔f(x)·g(x)≥0(≤0)且g(x)≠0.
以上两式的核心要义是将分式不等式转化为整式不等式.
重点难点突破
【题型一】一元二次不等式的求解
命题点1 不含参的不等式
【典型例题】
不等式x2+5x﹣6>0的解集是( )
A.{x|x<﹣2或x>3} B.{x|﹣2<x<3} C.{x|x<﹣6或x>l} D.{x|﹣6<x<l}
【解答】解:不等式x2+5x﹣6>0化为(x+6)(x﹣1)>0,
解得x<﹣6或x>1,
∴不等式的解集是{x|x<﹣6或x>1}.
故选:C.
【再练一题】
不等式6x2+17x+12<0的解集是 .
【解答】解:不等式6x2+17x+12<0可化为(2x+3)(3x+4)<0,
解得x,
∴所求不等式的解集是(,).
故答案为:(,).
命题点2 含参不等式
【典型例题】
设a>1,则关于x的不等式的解集是( )
A. B.(a,+∞)
C. D.
【解答】解:a>1时,1﹣a<0,且a,
则关于x的不等式可化为(x﹣a)(x)>0,
解得x或x>a,
所以不等式的解集为(﹣∞,)∪(a,+∞).
故选:D.
【再练一题】
已知不等式ax2+bx+c>0的解集是{x|α<x<β}(α>0),则不等式cx2+bx+a>0的解集是( )
A.(,) B.(﹣∞,)∪(,+∞)
C.{x|α<x<β} D.(﹣∞,α)∪(β,+∞)
【解答】解:不等式ax2+bx+c>0的解集是{x|α<x<β}(α>0),
则α,β是一元二次方程ax2+bx+c=0的实数根,且a<0;
∴α+β,α•β;
∴不等式cx2+bx+a>0化为x2x+1<0,
∴αβx2﹣(α+β)x+1<0;
化为(αx﹣1)(βx﹣1)<0;
又0<α<β,∴0;
∴不等式cx2+bx+a<0的解集为:{x|x}.
故选:A.
思维升华 含有参数的不等式的求解,往往需要对参数进行分类讨论.
(1)若二次项系数为常数,首先确定二次项系数是否为正数,再考虑分解因式,对参数进行分类讨论,若不易分解因式,则可依据判别式符号进行分类讨论.
(2)若二次项系数为参数,则应先考虑二次项系数是否为零,确定不等式是不是二次不等式,然后再讨论二次项系数不为零的情形,以便确定解集的形式;
(3)对方程的根进行讨论,比较大小,以便写出解集.
【题型二】一元二次不等式恒成立问题
命题点1 在R上的恒成立问题
【典型例题】
若不等式ax2﹣x+a>0对一切实数x都成立,则实数a的取值范围为( )
A.a或a B.a或a<0
C.a D.
【解答】解:不等式ax2﹣x+a>0对一切实数x都成立,
则,
即,
解得a,
所以实数a的取值范围是a.
故选:C.
【再练一题】
已知关于x的不等式x2﹣x+a﹣1≥0在R上恒成立,则实数a的取值范围是 .
【解答】解:关于x的不等式x2﹣x+a﹣1≥0在R上恒成立,
所以二次函数的图象与x轴最多有一个交点,
所以判别式△=(﹣1)2﹣4(a﹣1)≤0,
解得,
所以a的取值范围为.
故答案为:[,+∞).
命题点2 在给定区间上的恒成立问题
【典型例题】
已知[(m﹣1)x+1](x﹣1)>0,其中0<m<2,
(1)解不等式.
(2)若x>1时,不等式恒成立,求实数m的范围.
【解答】解:(1)[(m﹣1)x+1](x﹣1)>0
当m﹣1=0时,不等式为(x﹣1)>0即{x|x>1}.
当1﹣m<0时,即1<m<2,不等式解集为
当0<1﹣m<1时,即0<m<1,不等式解集为
综上得:当m=1时解集为{x|x>1},当0<m<1时解集为
当1<m<2时,不等式解集为
(2)x>1时,原命题化为(m﹣1)x+1>0恒成立,∴(m﹣1),∴1≤m<2
【再练一题】
已知关于x的不等式:x2﹣mx+m>0,其中m为参数.
(1)若该不等式的解集为R,求m的取值范围;
(2)当x>1时,该不等式恒成立,求m的取值范围.
【解答】解:(1)关于x的不等式x2﹣mx+m>0的解集为R,
则△<0,即m2﹣4m<0;……………………………
解得0<m<4,
∴m的取值范围是(0,4);……………………………
(2)当x>1时,关于x的不等式x2﹣mx+m>0恒成立,
等价于m恒成立,……………………………
设f(x),x>1;
则f(x)(x﹣1)2≥22=4,
当且仅当x=2时取“=”; ……………………………
∴m的取值范围是(﹣∞,4). ……………………………
命题点3 给定参数范围的恒成立问题
【典型例题】
已知不等式2x﹣1>m(x2﹣1).
(1)若对于所有实数x,不等式恒成立,求m的取值范围;
(2)若对于m∈[﹣2,2]不等式恒成立,求x的取值范围.
【解答】解:(1)原不等式等价于mx2﹣2x+(1﹣m)<0对任意实数x恒成立
当m=0时,﹣2x+1<0⇒x不恒成立
∴,
∴m无解.故m不存在.
(2)设f(m)=(x2﹣1)m﹣(2x﹣1)
要使f(m)<0在[﹣2,2]上恒成立,当且仅当
⇔
∴
∴x的取值范围是{x|}
【再练一题】
已知不等式mx2﹣2x﹣m+1<0.
(1)若对任意实数x上述不等式恒成立,求m的取值范围;
(2)若对一切m∈[﹣2,2]上述不等式恒成立,求x的取值范围.
【解答】解:(1)若对任意实数x上述不等式恒成立,
当m=0时,﹣2x+1<0显然不恒成立,
当m≠0时,要使对任意实数x上述不等式恒成立,
∴m<0,且△<0,
∴m2﹣m+1<0,解得x∈Φ;
故不存在m,使得mx2﹣2x﹣m+1<0对任意实数x上述不等式恒成立.
(2)若对一切m∈[﹣2,2]上述不等式恒成立,
设g(m)=m(x2﹣1)﹣2x+1,
∴g(﹣2)<0,且g(2)<0,
∴x,
故x的范围为x.
思维升华 (1)对于一元二次不等式恒成立问题,恒大于0就是相应的二次函数的图象在给定的区间上全部在x轴上方,恒小于0就是相应的二次函数的图象在给定的区间上全部在x轴下方.另外常转化为求二次函数的最值或用分离参数法求最值.
(2)解决恒成立问题一定要搞清谁是主元,谁是参数,一般地,知道谁的范围,谁就是主元,求谁的范围,谁就是参数.
跟踪训练
【题型三】一元二次不等式的应用
如果关于x的一元二次不等式ax2+bx+c>0的解集为{x|x<﹣2或x>4},那么对于函数应有( )
A.f(5)<f(2)<f(﹣1) B.f(2)<f(5)<f(﹣1)
C.f(﹣1)<f(2)<f(5) D.f(2)<f(﹣1)<f(5)
【解答】解:∵关于x的一元二次不等式ax2+bx+c>0的解集为{x|x<﹣2或x>4},
∴a>0,函数的对称轴为x=1,
∴f(﹣1)=f(3),函数在(1,+∞)上单调递增,
∴f(2)<f(3)<f(5),
∴f(2)<f(﹣1)<f(5),
故选:D.
【再练一题】
已知关于x的不等式x2﹣4ax+3a2<0(a<0)的解集为(x1,x2),则的最大值是( )
A. B. C. D.
【解答】解:不等式x2﹣4ax+3a2<0(a<0)的解集为(x1,x2),
根据韦达定理,可得:,x1+x2=4a,
那么:4a.
∵a<0,
∴﹣(4a)≥2,即4a
故的最大值为.
故选:D.
思维升华 求解不等式应用题的四个步骤
(1)阅读理解,认真审题,把握问题中的关键量,找准不等关系.
(2)引进数学符号,将文字信息转化为符号语言,用不等式表示不等关系,建立相应的数学模型.
(3)解不等式,得出数学结论,要注意数学模型中自变量的实际意义.
(4)回归实际问题,将数学结论还原为实际问题的结果.
基础知识训练
1.【贵州省铜仁市思南中学2018-2019学年高一下学期期中考试】不等式的解集为空集,则的取值范围是( )
A. B. C. D.
【答案】B
【解析】
因为不等式的解集为空集,
所以的图象与轴没有交点或有唯一交点,
有一个或没有实根,
,解得,
的取值范围是,故选B.
2.【北省宜昌市部分示范高中教学协作体2018-2019学年高一下学期期中考试】不等式的解集为,则的取值范围是( )
A. B. C. D.
【答案】C
【解析】
当时,不等式即,恒成立.
当时,由题意可得,且,解得.
综上,实数的取值范围是,故选C.
3.【安徽省安庆市第一中学2018-2019学年高一下学期期中考试】若不等式对一切实数都成立,则实数的取值范围为( )
A.或 B.或
C. D.
【答案】C
【解析】
解:显然a=0,不等式不恒成立,所以不等式对一切实数都成立,
则,
即,
解得,
所以实数的取值范围是.
故选:C.
4.【黑龙江省牡丹江市第一高级中学2018-2019学年高二下学期期中考试】不等式的解集为(-4,1),则不等式的解集为( )
A. B. C. D.
【答案】A
【解析】
不等式ax2+bx+c>0的解集为(﹣4,1),
则不等式对应方程的实数根为﹣4和1,且a<0;
由根与系数的关系知,,
∴,
∴不等式b(x2+1)﹣a(x+3)+c>0化为
3a(x2+1)﹣a(x+3)﹣4a>0,
即3(x2+1)﹣(x+3)﹣4<0,
解得﹣1<x,
∴该不等式的解集为(﹣1,).
故选:A.
5.【广东省佛山市南海区桂城中学2018-2019学年第二学期高一数学第二次阶段考试】已知关于的不等式的解集是,则的值是( )
A. B. C. D.
【答案】D
【解析】
关于的不等式的解集是
方程的解为:和
由根与系数的关系得:,,即
本题正确选项:
6.【广东省深圳市四校发展联盟体2018-2019学年高二第二学期期中考试】在R上定义运算,若对任意,不等式都成立,则实数的取值范围是( )
A. B.
C. D.
【答案】A
【解析】
由题意可得:
即:对任意恒成立
设
则(当且仅当,即时取等号)
即 ,即
本题正确选项:
7.【黑龙江省鹤岗市第一中学2018-2019学年高一下学期期中考试】在上定义运算,若存在使不等式成立,则实数的取值范围为
A. B. C. D.
【答案】C
【解析】
令
因为
即
也就是
在时,取最大值为6
所以
解得
故选C
8.【山东省济宁市2019届高三二模】已知函数,若不等式恒成立,则实数的取值范围为( )
A. B.
C. D.
【答案】D
【解析】
由函数的解析式易知恒成立,则,
原问题等价于函数的图像恒不在函数图像的下方;
绘制函数的图像,如图所示,
函数表示过定点的直线,很明显时不满足题意,时满足题意,
当时,考查如图所示的临界条件,即直线与二次函数相切,
,设切点坐标为,切线的斜率为,
则切线方程过点,
即:,
数形结合可知,故,此时切线的斜率,
故实数的取值范围为.
故选:D.
9.【江西师范大学附属中学2018-2019学年高一下期期中考试】已知正实数满足,若对任意满足条件的,都有恒成立,则实数的最大值为( )
A. B.7 C. D.8
【答案】B
【解析】
,且,
故,整理即,
又均为正实数,故,
又对于任意满足的正实数,均有恒成立,
整理可得恒成立,令,
令,时
所以在上递增,
,因此,
实数的最大值为7,故选B.
10.【湖北省荆州市沙市中学2018-2019学年高一5月月考】若正实数,满足,且恒成立,则实数的取值范围为( )
A. B. C. D.
【答案】B
【解析】
由题意知:
, ,
(当且仅当,即时取等号)
,解得:
本题正确选项:
11.【福建省上杭县第一中学2018-2019学年高一5月月考】若两个正实数,满足,且不等式有解,则实数的取值范围为( )
A. B.
C. D.
【答案】B
【解析】
由题有解
,当且仅当y=2,x=4等号成立
则,解得实数的取值范围为
故选:B
12.【河北廊坊2018-2019学年高一年级第二学期期中联合调研考试高一】已知函数,如果不等式的解集为,那么不等式的解集为( )
A. B.
C. D.
【答案】A
【解析】
解:由的解集是,则
故有,即.
由
解得
故不等式的解集是
故选A.
13.【内蒙古包头市第九中学2018-2019学年高一下学期期中考试】二次不等式的解集为,则的值为_______.
【答案】6
【解析】
二次不等式的解集为,
则,且的两个根为和.
所以,解得.
所以
14.【贵州省凯里市第一中学2018-2019学年高一下学期期中考试】已知不等式的解集为,则的最小值为__________.
【答案】8
【解析】
由题知,则,
则=8,当且仅当,
即时取等号.故的最小值为8.
故答案为:8
15.【内蒙古赤峰二中2018-2019学年高一下学期第二次月考】不等式的解集为 或 ,则实数a的取值范围______.
【答案】
【解析】
由题意可得和是方程的根,
又,
所以,故.
16.【江西省南昌市第十中学2018-2019学年高一下学期第二次月考】已知关于的不等式的解集是,则的解集为_____.
【答案】
【解析】
由题意,关于的不等式的解集是,
则,解得,
所以不等式,即为,
即,即,解得
即不等式的解集为.
17.【四川省大竹中学2018-2019学年高一第二学期5月月考考前模拟】已知函数.
(1)求关于的不等式的解集;
(2)若不等式对任意恒成立,求实数的取值范围.
【答案】(1) (2)
【解析】
(1)由得,即,
所以的解集为;
(2)不等式对任意恒成立,
由
得,的最小值为1,
所以恒成立,即,
所以,
所以实数的取值范围为.
18.【福建省三明市三地三校2018-2019学年高一下学期期中联考】已知函数
(1)解不等式;
(2)若对一切,不等式恒成立,求实数的取值范围.
【答案】(1);(2)
【解析】
(1) 或
所求不等式解集为:
(2)当时,可化为:
又(当且仅当,即时取等号)
即的取值范围为:
19.【内蒙古赤峰市2018-2019学年高一下学期期中考试】已知函数.
(1)当m=-4时,解不等式;
(2)若m>0,的解集为(b,a),求的最大値.
【答案】(1) [4,1];(2)-3
【解析】
(1)当m=﹣4时,不等式f(x)≤0,即为x2+3x﹣4≤0,可得:(x+4)(x﹣1)≤0,即不等式f(x)≤0的解集为[﹣4,1].
(2)由题的根即为a,b,故a+b=-3,ab=m>0,故a,b同负,
则= 当且仅当 等号成立
20.【黑龙江省哈尔滨市呼兰一中、阿城二中、宾县三中、尚志五中四校2018-2019学年高一下学期期中考试】已知函数.
(1)当时,求不等式的解集
(2)若对于任意,恒成立,求实数的取值范围.
【答案】(1)(2)
【解析】
(1)
即不等式的解集为,
(2)时取最小值,
因此
21.【安徽省固镇县第一中学2018-2019学年高二5月月考】设命题:实数满足;命题:实数满足
(1)若,且为真,求实数的取值范围;
(2)若,且是的充分不必要条件,求实数的取值范围.
【答案】(1) (2)
【解析】
解:(1)由得;
当时,,即P为真时,
由得,即,即q为真时,
因为为真,则p真q真,所以
(2)由得;,又,
所以m<x<3m,
由得,即;
设,
若的充分不必要条件
则A是B 的真子集,所以即
22.【湖北省荆州市沙市中学2018-2019学年高一5月月考】设函数
(I)若,且对于,有恒成立,求的取值范围;
(II)若,解关于的不等式
【答案】(I);(II)见解析.
【解析】
(I)当时,,此时
当时,恒成立, 即恒成立
设,则且,
函数在区间上是单调递减的
综上所述:
(II) 解不等式即解不等式
当时,原不等式等价于,解得:
当时,原不等式等价于
令,解得:,
若,则,解得:或
若,则,解得:
若则,解得:或
若,则,解得:
综上,当,不等式的解集为;当时,不等式的解集为;当时,不等式的解集为;当
时,不等式的解集为;当时,不等式的解集为
能力提升训练
1.【2019年河北省藁城市第一中学高一下学期7月月考】设,则关于的不等式的解集是( )
A. B.
C. D.
【答案】D
【解析】
a>1时,1﹣a<0,且a,
则关于x的不等式可化为(x﹣a)(x)>0,
解得x或x>a,
所以不等式的解集为(﹣∞,)∪(a,+∞).
故选:D.
2.【河南省濮阳市2018-2019学年高二下学期升级考试】设是关于的一元二次方程的两个实根,则的最小值是( )
A. B.18 C.8 D.-6
【答案】C
【解析】
因为是关于的一元二次方程的两个实根
所以由韦达定理得 ,且
所以
且或
由二次函数的性质知,当时,函数取得最小值为
即的最小值为
故选C.
3.【江苏省无锡市锡山区天一中学2019年高一期末】已知关于的不等式对任意恒成立,则的取值范围是( )
A. B. C.或 D.或
【答案】A
【解析】
当时,不等式为恒成立,符合题意;
当时,若不等式对任意恒成立,
则,解得;
当时,不等式不能对任意恒成立。
综上,的取值范围是.
4.【江西省南昌市东湖区第二中学2018-2019学年高二下学期期末】已知,且,若对任意的正数,不等式恒成立,则实数的取值范围是( )
A.或 B.或
C. D.
【答案】D
【解析】
,
当且仅当,即时取等号
,解得:
本题正确选项:
5.【宁夏回族自治区银川一中2018-2019高二下学期期中考试】若存在,使不等式成立,则实数取值范围是( )
A. B. C. D.
【答案】C
【解析】
令,对称轴方程为,
若存在,使不等式成立,
等价于,
当时,即,,解得,
因为,所以;
当时,即,,解得,
因为,所以;
因为,所以.
故选C.
6.【浙江省绍兴市第一中学2018-2019学年高二下学期期中考试】已知,若关于的不等式>的解集中的整数恰有3个,则的取值范围为( )
A. B. C. D.
【答案】C
【解析】
因为>,所以,
因为,且解集中的整数恰有3个,
所以
因为,所以,
从而,即,
因为,所以,选C.
7.【安徽省淮南市第一中学2018-2019年高一年级第二学期第二次段考】已知关于的不等式的解集为.
(1)求实数的值;
(2)解关于的不等式.(为常数)
【答案】(1) ; (2)见解析
【解析】
(1)由不等式解集为得方程仅有一解,由得,,
从而.
(2)原不等式可以变形为,所以
当时,原不等式的解集为;
当时,原不等式的解集为;
当时,原不等式的解集为.
8.【浙江省嘉兴市2018-2019学年高一下学期期末考试】已知函数.
(Ⅰ)当时,解不等式;
(Ⅱ)当时,恒成立,求的取值范围.
【答案】(Ⅰ);(Ⅱ).
【解析】
(Ⅰ)当时,一元二次不等式的解为,故不等式的解集为.
(Ⅱ)当时,恒成立,
即恒成立,令
因,当时等号成立,故的最大值为,故.
9.【浙江“七彩阳光”新高考研究联盟2018-2019学年高一下学期期中考试】设函数.
(Ⅰ)当时,解不等式:;
(Ⅱ)当时,存在最小值,求的值.
【答案】(Ⅰ);(Ⅱ)1.
【解析】
设2x=t(t>0),则,
(Ⅰ)当时,,即或
∵t>0,∴2x>8,即x>3,
∴不等式的解集是:{x|x>3}.
(Ⅱ)当时,必有对称轴,即0<<2,
最小值为,化简得,
由于关于的函数单调递增,故最多有一个实根。
而当时,所以的值为1.
10.【安徽省淮南市第一中学2018-2019年高一年级第二学期第二次段考】设函数,.已知关于的不等式的解集恰好为.
(1)求;
(2)对于使得恒成立,求实数的取值范围.
【答案】(1) (2)
【解析】
(1)由题意知:的二根为、
即:的二根为、
(舍)或
满足题意
故
(2)
又当且仅当 等号成立