数学文卷·2019届安徽省滁州市定远县育才学校高二上学期期末考试（2018-02）

数学文卷·2019届安徽省滁州市定远县育才学校高二上学期期末考试（2018-02）

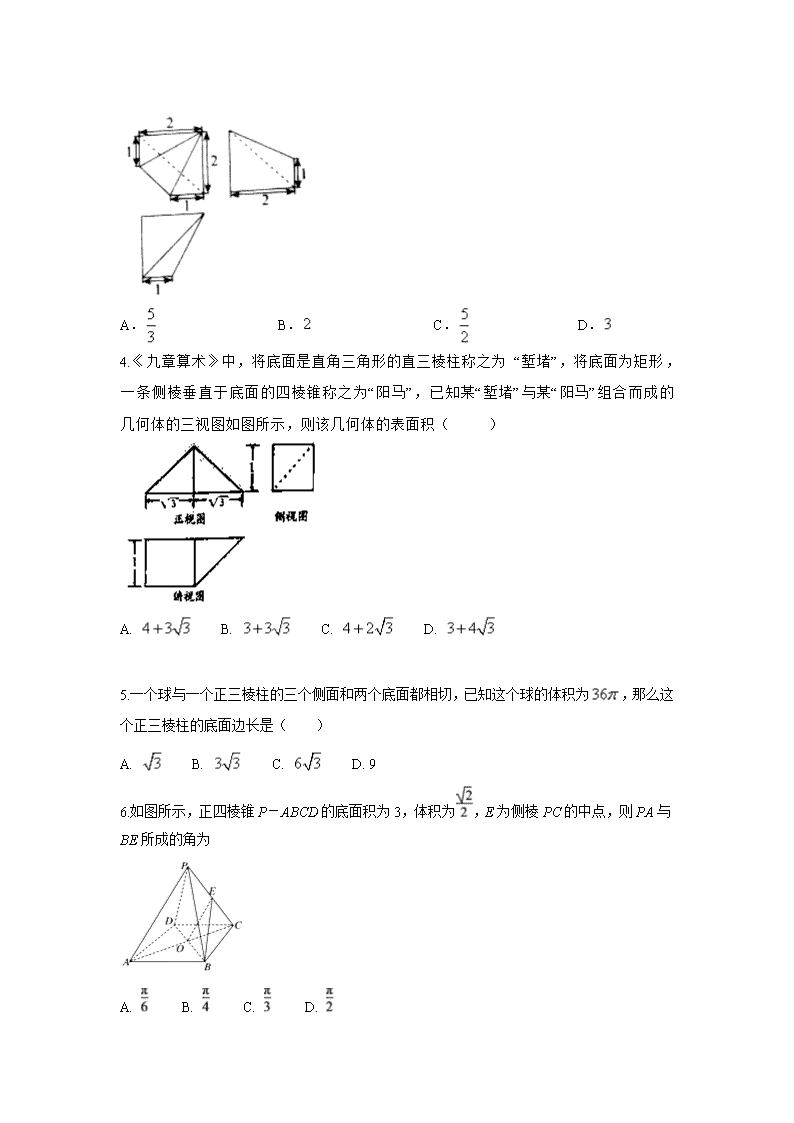
定远育才学校2017-2018学年第一学期期末考试 高二数学（文科）试题 考生注意：‎ ‎1.本卷分第I卷和第II卷，满分150分，考试时间120分钟。答题前，先将自己的姓名、准考证号填写在试题卷和答题卷上。‎ ‎2.选择题的作答：每小题选出答案后，用2B铅笔把答题卷上对应题目的答案标题涂黑。‎ ‎3.非选择题的作答:用签字笔直接答在答题卷上对应的答题区内。‎ 第I卷（选择题60分）‎ 一、选择题 ‎1. 已知表示两条不同直线，表示平面．下列说法正确的是 A．若则 B．若，则 C．若则 D．若，则 ‎2.一空间几何体的三视图如图所示, 该几何体的体积为，则正视图中的值为（ ）‎ A. B. C. D．‎ ‎3. 某几何体的三视图如图所示, 则该几何体的体积为（ ）‎ A． B． C． D．‎ ‎4.《九章算术》中，将底面是直角三角形的直三棱柱称之为“堑堵”，将底面为矩形，一条侧棱垂直于底面的四棱锥称之为“阳马”，已知某“堑堵”与某“阳马”组合而成的几何体的三视图如图所示，则该几何体的表面积（ ）‎ A. B. C. D. ‎ ‎5.一个球与一个正三棱柱的三个侧面和两个底面都相切，已知这个球的体积为，那么这个正三棱柱的底面边长是（ ）‎ A. B. C. D. 9‎ ‎6.如图所示，正四棱锥P－ABCD的底面积为3，体积为，E为侧棱PC的中点，则PA与BE所成的角为 A. B. C. D. ‎ ‎7. 为三条不重合的直线，α、β、γ为三个不重合平面，现给出六个命题：‎ ‎① ；②；③；‎ ‎④；⑤；⑥‎ 其中正确的命题是(　　)‎ A. ①②③ B. ①④⑤ C. ①④ D. ①③④‎ ‎8.某几何体的正视图、俯视图和侧视图中，某条棱的投影长分别为，则该条棱的长度为( )‎ A. B. C. D. ‎ ‎9. 如图正方形折成直二面角，则二面角的余弦值为（ ）‎ A. B. C. D. ‎ ‎10.某四面体的三视图如图所示，该四面体四个面的面积中，最大的是（ ）．‎ ‎ ‎ A. B. C. D. ‎ ‎11.过正方体的顶点作直线，使直线分别与三条棱所成的角都相等，则这样的直线有（ ）条 A. B. C. D. ‎ ‎12. 在正方体中， 为的中点， 为的中点，则异面直线与所成角的正切值为（ ）‎ A. B. C. D. ‎ 第II卷（非选择题）‎ 二、填空题 ‎13. 如图所示，在正方体ABCD－A1B1C1D1中，M、N分别是棱AA1和AB上的点，若∠B1MN是直角，则∠C1MN等于____.‎ ‎14.底面为正三角形的直三棱柱ABC-A1B1C1的各棱长都为1，M,N分别为CC1，BB1的中点，则点N到面A1BM的距离为__________．‎ ‎15.已知水平放置的△ABC是按“斜二测画法”得到如下图所示的直观图，其中， ,则原△ABC的面积为_______‎ ‎16. 已知直线平面且⊥， ，给出下列四个命题：‎ ‎①若∥，则⊥；②若⊥，则∥；‎ ‎③若⊥，则∥；④若∥，则⊥‎ 其中正确的命题有_________‎ 三、解答题 ‎17.如图所示的立体图形中，，．‎ ‎（Ⅰ）证明：；‎ ‎（Ⅱ）若，，求二面角的余弦值．‎ ‎18.如图，平面五边形中， ∥，， .将沿折起，使点到的位置，且，得到四棱锥.‎ ‎（1）求证： 平面；‎ ‎（2）记平面与平面相交于直线，求证：∥.‎ ‎19.在长方体中， ， ， ，点在棱上移动.‎ ‎（Ⅰ）当时，求证：直线平面；‎ ‎（Ⅱ）在（Ⅰ）的条件下，求的值.‎ ‎20.如图，在三棱锥中， ⊥平面， ， ， ， 分别为的中点．(19)‎ ‎(I)求到平面的距离；‎ ‎(II)在线段上是否存在一点，使得平面∥平面，若存在，试确定的位置，并证明此点满足要求；若不存在，请说明理由．‎ ‎21.如下图，三棱柱中，侧面 底面， ,且,O为中点.‎ ‎（Ⅰ）证明： 平面；‎ ‎（Ⅱ）求直线与平面所成角的正弦；‎ ‎（Ⅲ）在上是否存在一点，使得平面，若不存在，说明理由；若存在，确定点的位置.‎ ‎22.如图，在直三棱柱中， ， ， 分别是的中点。‎ ‎ （Ⅰ）求证： ；‎ ‎ （Ⅱ）求直线和平面所成角的大小．‎ 定远育才学校2017-2018学年第一学期期末考试 高二数学（文科）试题答案 一、选择题 ‎1.B 2. C 3.B 4. A 5. C 6. C 7.C 8. A 9.B 10.C 11.D 12.C 二、填空题 ‎13. 90°‎ ‎14. ‎ ‎15. ‎ ‎16. ①④‎ 三、解答题 ‎17.‎ ‎（Ⅰ）证明：在图2中取的中点，‎ 连接，，‎ 因为，所以，‎ 又因为，‎ 所以，‎ 因为，所以平面，‎ 而平面，所以．‎ ‎（Ⅱ）由（Ⅰ）知，，‎ 因为，，‎ 所以，‎ 因为，所以，‎ 所以为等腰直角三角形，且，，‎ 所以，‎ 以为原点，直线，，分别为，，轴 建立空间直角坐标系，则，，，，‎ 所以，，可求得平面的一个法向量为，‎ 易知是平面的一个法向量，‎ 所以，‎ 因为二面角为锐角，故二面角的余弦值为．‎ ‎18.‎ ‎（1）在中，∵， ，由余弦定理得.‎ 连接，∵.‎ 又∵，∴在中， ，即.‎ 同理， ， 平面， ，故平面.‎ ‎（2）∵∥，且平面， 平面，‎ ‎∴∥平面，又平面平面 ，∴∥.‎ ‎19. ‎ ‎（Ⅰ）证明：连接因为四边形为正方形，所以，‎ 又平面， 平面，‎ 所以，又，‎ 所以平面，所以.‎ 在上取一点，使，连接， ，‎ 易证，所以，‎ 又， ，‎ 所以平面，所以，‎ 又，且，所以平面.‎ ‎（Ⅱ）因为 ，‎ 且两个三棱锥的底面相同，所以体积比等于相应的高之比.‎ ‎，‎ 设点到平面的距离为，‎ 由，可得 ，则，‎ 故点到平面的距离为，所以 .‎ ‎20. ‎ ‎(I)因为平面 ，所以，‎ 即与为直角三角形．‎ 又因为, ‎ 所以. ‎ 由,可知为直角三角形．‎ 所以，所以,‎ 设到平面的距离为，‎ 由于，得，解得 ‎ ‎(II)在线段上存在一点，使得平面平面，此时为线段的中点．‎ 证明过程：如图，连接，因为分别为的中点，所以.‎ 又平面上，所以平面. ‎ 因为分别为的中点，所以.‎ 又平面，所以平面， ‎ 又平面， 平面，‎ 所以平面∥平面. ‎ ‎21. ‎ ‎(Ⅰ)证明:因为,且O为AC的中点,‎ 所以 又由题意可知,平面平面,交线为,且平面,‎ 所以平面 ‎(Ⅱ)如图,以O为原点, 所在直线分别为x,y,z轴建立空间直角坐标系.‎ 由题意可知, 又 ‎ 所以得: ‎ 则有: ‎ 设平面的一个法向量为,则有 ‎,令,得 所以 因为直线与平面所成角和向量与所成锐角互余,所以 ‎(Ⅲ)设 即,得 所以得 令平面,得,‎ 即得 即存在这样的点E,E为的中点 ‎22.‎ ‎（I）证明：由已知 ‎∴平面 连接，则 ‎ ‎ 由已知，侧面是正方形，所以 ‎ 又∵‎ ‎∴平面 ‎∵侧面是正方形， 是的中点 ‎∴连接，则点是的中点 又∵点N是的中点 ‎∴是的中位线 ‎∴∥‎ ‎∴平面 ‎ （Ⅱ）设与相交于点，连接 ‎∵平面 ‎∴为直线和平面所成角 设，则在 ‎ ‎ ‎∴， 故直线和平面所成的角为30°‎