江苏省天一中学2020届高三上学期10月份调研考试数学试题 含解析

江苏省天一中学2020届高三上学期10月份调研考试数学试题 含解析

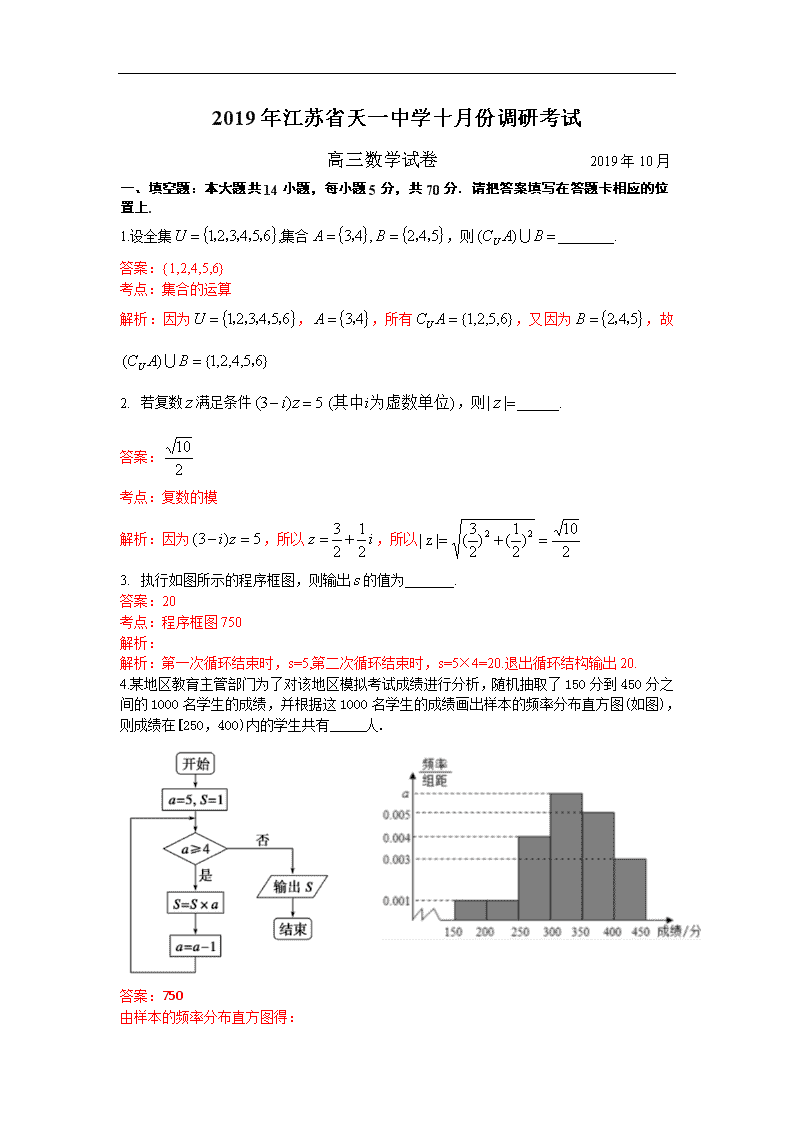
‎2019年江苏省天一中学十月份调研考试 ‎ 高三数学试卷 2019年10月 一、填空题：本大题共14小题，每小题5分，共70分．请把答案填写在答题卡相应的位置上.‎ ‎1.设全集,集合,，则________.‎ 答案：{1,2,4,5,6}‎ 考点：集合的运算 解析：因为，，所有，又因为，故 2. 若复数满足条件，则______.‎ 答案：‎ 考点：复数的模 解析：因为，所以，所以 3. 执行如图所示的程序框图，则输出的值为_______.‎ 答案：20‎ 考点：程序框图750‎ 解析：‎ 解析：第一次循环结束时，s=5,第二次循环结束时，s=5×4=20.退出循环结构输出20.‎ ‎4.某地区教育主管部门为了对该地区模拟考试成绩进行分析，随机抽取了150分到450分之间的1000名学生的成绩，并根据这1000名学生的成绩画出样本的频率分布直方图(如图)，则成绩在[250，400)内的学生共有_____人.‎ ‎ ‎ 答案：750‎ 由样本的频率分布直方图得： （0.001＋0.001＋0.004＋a＋0.005＋0.003）×50＝1， 解得a＝0.006． ∴成绩在[250，400）内的频率为（0.004＋0.006＋0.005）×50＝0.75， ∴成绩在[250，400）内的学生共有1000×0.75＝750． 故答案为：750．‎ ‎5.口袋中有形状和大小完全相同的4个球，球的编号分别为1,2,3,4.若从袋中一次随机摸出2个球，则摸出的2个球的编号之和大于4的概率为______.‎ 答案：‎ 考点：古典概型及其概率计算公式 解析：口袋中有形状和大小完全相同的4个球，球的编号分别为1,2,3,4, 从袋中一次随机摸出2个球，基本事件总数n==6‎ 摸出的2个球的编号之和大于4包含的基本事件有:(1,4)，(2,3),(2，4)，(3,4)，共4个,摸出的2个球的编号之和大于4的概率为 ‎6.已知为奇函数，为偶函数，则_____.‎ 答案：‎ 考点：函数奇偶性的性质 解析：由为奇函数，求出,为偶函数，求出，所以 ‎7.若函数图像的两条相邻的对称轴之间的距离为，且该函数图像关于点成中心对称，，则______.‎ 答案：‎ 考点：函数的图像变换 8. 在等差数列中，为前n项和，已知，,则公差的值为______.‎ 答案：-3‎ 考点：等差数列的性质 解析：因为，所以.又因为,所以，所以 ‎，‎ 8. 设甲、乙两个圆柱的底面积分别为,体积分别为，若它们的侧面积相等，,则_____.‎ 答案：‎ 考点：旋转体（圆柱、圆锥、圆台）‎ 9. 向量均为非零向量，，则与的夹角为_____.‎ 答案：‎ 考点：数量积表示两个向量的夹角 11. 已知，则______.‎ 答案：‎ 考点：三角恒等变换 解析：令，则，所以 所以，因为 所以，所以.‎ 11. 已知定义在上的可导函数的导函数为，满足，且，则关于的不等式的解集为______.‎ 答案：‎ 考点：导数研究函数的单调性 解析：，，因为，所以 所以，因为，因为，‎ 求得 12. 点B在线段AC上，，点P是A、B、C所在直线外一点，且满足，，则_____.‎ 答案：‎ 考点：向量的基本运算 13. 已知实数x,y>0，则的最大值为______.‎ 答案：‎ 考点：基本不等式 解析：‎ ‎(当且仅当“”时取“=”)‎ 二、解答题：本大题共6小题，共计90分，请在答题卡指定区域内作答，解答时应写出文字说明、证明或演算步骤.‎ ‎15. (本小题满分14分)‎ 设向量，，.(其中)‎ (1) 若，求实数的值；‎ (2) 若，求的值.‎ ‎16. (本小题满分14分)‎ 如图，已知A、B、C、D四点共面，且CD=1，BC=2，AB=4，，.‎ (1) 求;‎ (2) 求AD.‎ ‎17. (本小题满分14分)‎ 在如图所示的空间几何体中，四边形ABCD为正方形，四边形ABEF为直角梯形，已知AF∥BE，AB⊥BE，平面ABEF⊥平面ABCD，AB=BE=2AF，点P为棱DE上一点，且DP=2PE.‎ (1) 求证：AC∥平面DEF；‎ (2) 求证：BP⊥平面DEF.‎ ‎(2）设AF= x,则AB=BE=2x ‎ ‎ ‎18. (本小题满分16分)‎ 政府部门为加快实现塌陷区域整治和资源枯竭城市转型发展，对一片半径为1km的圆形采煤塌陷区进行生态修复和景观建设，将其开发为湿地景区.一期工程对塌陷区水面及周边整治已结束，二期工程是进行湖面观光曲桥建设，设计方案如下:在圆形水面上建设由线段AB、AP、BP、CD组成的环湖观光曲桥，其中A、B、P是湖面观光曲桥的出入口，出入口A建在湖面东西方向的正东的湖边，出入口B建在湖面南北方向方向的正北的湖边，出入口P建在圆形湖面南偏西的某处湖边，C、D分别在东西和南北方向的轴线上，满足P、C、B共线，P、D、A共线.  (1)求曲桥AB、BC、CD、DA围成的水域的面积;  (2)试确定P点的位置，使得曲桥CD、DP、PC围成的水域面积最大.‎ ‎19. (本小题满分16分)‎ 已知:对于无穷数列与,记，，若同时满足条件:①，均单调递增；②且，则称与是无穷互补数列. (1)若,判断与是否为无穷互补数列，并说明理由；‎ ‎(2)若且与是无穷互补数列，求数列的前16项的和;‎ ‎ (3)若与是无穷互补数列，为等差数列且，求与的通项公式.‎ ‎20. (本小题满分16分)‎ 已知函数.‎ (1) 若，求函数的极小值；‎ (2) 若在的最小值为0，求实数的取值范围；‎ (3) 若对任意的恒成立，求实数的取值范围.‎ ‎0‎ ‎0‎ 增 极大值 减 极小值 增