【数学】2018届一轮复习人教A版命题与量词、基本逻辑联结词学案

【数学】2018届一轮复习人教A版命题与量词、基本逻辑联结词学案

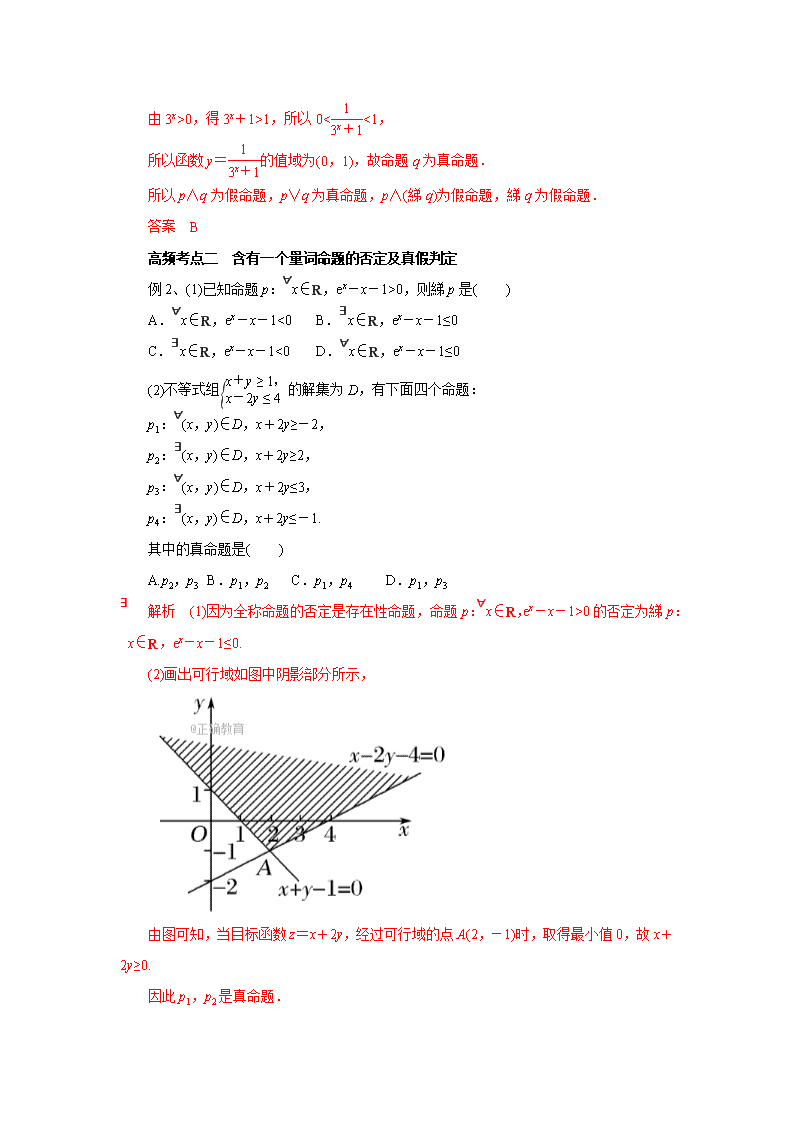
专题02 命题与量词、基本逻辑联结词（教学案） ‎ ‎1.理解全称量词与存在量词的意义；‎ ‎2.能正确地对含有一个量词的命题进行否定；‎ ‎3.了解命题的概念，了解逻辑联结词“或”、“且”、“非”的含义．‎ ‎ ‎ ‎1．命题 能判断真假的语句叫做命题．‎ ‎2．全称量词与全称命题 ‎(1)全称量词：短语“所有”在陈述中表示所述事物的全体，在逻辑中通常叫做全称量词．‎ ‎(2)全称命题：含有全称量词的命题．‎ ‎(3)全称命题的符号表示 形如“对M中所有x，p(x)”的命题，可用符号简记为“∀x∈M，p(x)”．‎ ‎3．存在量词与存在性命题 ‎ ‎(1)存在量词：短语“有一个”或“有些”或“至少有一个”在陈述中表示所述事物的个体或部分，逻辑中通常叫做存在量词。‎ ‎(2)存在性命题：含有全称量词的命题． ‎ ‎(3)存在性命题的符号表示 ‎ 形如“存在集合M中的元素x，q(x)”的命题，用符号简记为 ∃x∈M，q(x)。‎ ‎4．基本逻辑联结词 ‎ 常用的基本逻辑联结词有“且”、“或”、“非”． ‎ ‎5．命题p∧q，p∨q，綈p的真假判断 ‎ p ‎ q ‎ p∧q ‎ p∨q ‎ 綈p ‎ 真 ‎ 真 ‎ 真 ‎ 真 ‎ 假 ‎ 真 ‎ 假 ‎ 假 ‎ 真 假 ‎ 假 ‎ 真 ‎ 假 ‎ 真 ‎ 真 ‎ 假 ‎ 假 ‎ 假 ‎ 假 ‎ 真 ‎ ‎6．含有一个量词的命题的否定 命题 ‎ 命题的否定 ‎ ‎∀x∈M，p(x) ‎ ‎∃x∈M，綈p(x) ‎ ‎∃x∈M，p(x) ‎ ‎∀x∈M，綈p(x) ‎ 高频考点一　含有逻辑联结词的命题的真假判断 例1、设a，b，c是非零向量．已知命题p: 若a·b＝0，b·c＝0，则a·c＝0；命题q：若a∥b，b∥c，则a∥c.则下列命题中真命题是(　　)‎ A．p∨q B．p∧q C．(綈p)∧(綈q) D．p∧(綈q)‎ 解析　取a＝c＝(1，0)，b＝(0，1)，显然a·b＝0，b·c＝0，但a·c＝1≠0，∴p是假命题．‎ 又a，b，c是非零向量，‎ 由a∥b知a＝xb，由b∥c知b＝yc，‎ ‎∴a＝xyc，∴a∥c，∴q是真命题．‎ 综上知p∨q是真命题，p∧q是假命题．‎ 又∵綈p为真命题，綈q为假命题．‎ ‎∴(綈p)∧(綈q)，p∧(綈q)都是假命题．‎ 答案　A ‎【感悟提升】(1)“p∨q”、“p∧q”、“綈p”形式命题真假的判断关键是对逻辑联结词“或”“且”“非”含义的理解，其操作步骤是：①明确其构成形式；②判断其中命题p，q的真假；③确定“p∨q”“p∧q”“綈p”形式命题的真假．‎ ‎(2)p且q形式是“一假必假，全真才真”，p或q形式是“一真必真，全假才假”，非p则是“与p的真假相反”．‎ ‎【变式探究】命题p：函数y＝log2(x－2)的单调增区间是[1，＋∞)，命题q：函数y＝的值域为(0，1)．下列命题是真命题的为(　　)‎ A．p∧q B．p∨q C．p∧(綈q) D．綈q 解析　由于y＝log2(x－2)在(2，＋∞)上是增函数，‎ ‎∴命题p是假命题．‎ 由3x>0，得3x＋1>1，所以0<<1，‎ 所以函数y＝的值域为(0，1)，故命题q为真命题．‎ 所以p∧q为假命题，p∨q为真命题，p∧(綈q)为假命题，綈q为假命题．‎ 答案　B 高频考点二　含有一个量词命题的否定及真假判定 例2、(1)已知命题p：∀x∈R，ex－x－1>0，则綈p是(　　)‎ A．∀x∈R，ex－x－1<0 B．∃x∈R，ex－x－1≤0‎ C．∃x∈R，ex－x－1<0 D．∀x∈R，ex－x－1≤0‎ ‎(2)不等式组的解集为D，有下面四个命题：‎ p1：∀(x，y)∈D，x＋2y≥－2，‎ p2：∃(x，y)∈D，x＋2y≥2，‎ p3：∀(x，y)∈D，x＋2y≤3，‎ p4：∃(x，y)∈D，x＋2y≤－1.‎ 其中的真命题是(　　)‎ A.p2，p3 B．p1，p2 C．p1，p4 D．p1，p3‎ 解析　(1)因为全称命题的否定是存在性命题，命题p：∀x∈R，ex－x－1>0的否定为綈p：∃x∈R，ex－x－1≤0.‎ ‎(2)画出可行域如图中阴影部分所示，‎ 由图可知，当目标函数z＝x＋2y，经过可行域的点A(2，－1)时，取得最小值0，故x＋2y≥0.‎ 因此p1，p2是真命题．‎ 答案　(1)B　(2)B ‎【感悟提升】(1)全称命题与存在性命题的否定与命题的否定有一定的区别，否定全称命题和存在性命题时，一是要改写量词，全称量词改写为存在量词，存在量词改写为全称量词；二是要否定结论，而一般命题的否定只需直接否定结论．‎ ‎(2)判定全称命题“∀x∈M，p(x)”是真命题需要对集合M中的每一个元素x，证明p(x)成立；要判断存在性命题是真命题，只要在限定集合内至少找到一个x，使p(x)成立．‎ ‎【变式探究】命题p：存在x∈，使sin x＋cos x>；命题q：“∃x∈(0，＋∞)，ln x＝x－1”的否定是“∀x∈(0，＋∞)，ln x≠x－1”，则四个命题：(綈p)∨(綈q)，p∧q，(綈p)∧q，p∨(綈q)中，正确命题的个数为(　　)‎ A．1 B．2 C．3 D．4‎ 解析　因为sin x＋cos x＝sin≤，所以命题p是假命题；又存在性命题的否定是全称命题，因此命题q为真命题．则(綈p)∨(綈q)为真命题，p∧q为假命题，(綈p)∧q为真命题，p∨(綈q)为假命题．‎ ‎∴四个命题中正确的有2个命题．‎ 答案　B 高频考点三　由命题的真假求参数的取值范围 例3、(1)已知命题“∃x∈R，使2x2＋(a－1)x＋≤0”是假命题，则实数a的取值范围是(　　)‎ A．(－∞，－1) B．(－1，3) C．(－3，＋∞) D．(－3，1)‎ ‎(2)已知p：∃x∈R，mx2＋1≤0，q：∀x∈R，x2＋mx＋1＞0，若p∨q为假命题，则实数m的取值范围是(　　)‎ A．[2，＋∞) B．(－∞，－2]‎ C．(－∞，－2]∪[2，＋∞) D．[－2，2]‎ ‎【感悟提升】　(1)根据含逻辑联结词的命题真假求参数的方法步骤：‎ ‎①根据题目条件，推出每一个命题的真假(有时不一定只有一种情况)；‎ ‎②求出每个命题是真命题时参数的取值范围；‎ ‎③根据每个命题的真假情况，求出参数的取值范围．‎ ‎(2)全称命题可转化为恒成立问题．‎ ‎【变式探究】设p：实数x满足x2－5ax＋4a2<0(其中a>0)，q：实数x满足20，q：“x>‎1”‎是“x>‎2”‎的充分不必要条件，则下列命题为真命题的是(　　)‎ A．p∧q B．綈p∧綈q ‎ C．綈p∧q D．p∧綈q ‎【答案】D　‎ ‎【解析】根据指数函数的图像可知p为真命题．由于“x>‎1”‎是“x>‎‎2”‎ 的必要不充分条件，所以q为假命题，所以綈q为真命题，所以p∧綈q为真命题． ‎ ‎【2013·湖北卷】在一次跳伞中，甲、乙两位学员各跳一次，设命题p是“甲降落在指定范围”，q是“乙降落在指定范围”，则命题“至少有一位学员没有降落在指定范围”可表示为(　　)‎ A．(p)∨(q) B．p∨(q)‎ C．(p)∧(q) D．p∨q ‎【答案】A　‎ ‎【解析】“至少一位学员没降落在指定区域”即“甲没降落在指定区域或乙没降落在指定区域”，可知选A.‎ ‎1．已知命题p：所有指数函数都是单调函数，则綈p为(　　)‎ A．所有的指数函数都不是单调函数 B．所有的单调函数都不是指数函数 C．存在一个指数函数，它不是单调函数 D．存在一个单调函数，它不是指数函数 解析　命题p：所有指数函数都是单调函数，则綈p为：存在一个指数函数，它不是单调函数．‎ 答案　C ‎2．设命题p：函数y＝sin 2x的最小正周期为；命题q：函数y＝cos x的图象关于直线x＝对称．则下列判断正确的是(　　)‎ A．p为真 B．綈p为假 C．p∧q为假 D．p∧q为真 解析　p为假命题，q为假命题，∴p∧q为假．‎ 答案　C ‎3．2016年巴西里约奥运会，在体操预赛中，有甲、乙两位队员参加．设命题p是“甲落地站稳”，q是“乙落地站稳”，则命题“至少有一位队员落地没有站稳”可表示为(　　)‎ A．(綈p)∨(綈q) B．p∨(綈q) C．(綈p)∧(綈q) D． p∨q ‎4．已知命题p：对任意x∈R，总有|x|≥0；q：x＝1是方程x＋2＝0的根．则下列命题为真命题的是(　　)‎ A．p∧(綈q) B．(綈p)∧q C．(綈p)∧(綈q) D．p∧q 解析　由题意知命题p是真命题，命题q是假命题，故綈p是假命题，綈q是真命题，由含有逻辑联结词的命题的真值表可知p∧(綈q)是真命题．‎ 答案　A ‎5．下列命题中，真命题是(　　)‎ A．∃x∈R，ex≤0‎ B．∀x∈R，2x>x2‎ C．a＋b＝0的充要条件是＝－1‎ D．“a>1，b>1”是“ab>1”的充分条件 解析　因为y＝ex>0，x∈R恒成立，所以A不正确．‎ 因为当x＝－5时，2－5<(－5)2，所以B不正确．‎ ‎“＝－1”是“a＋b＝0”的充分不必要条件，C不正确．‎ 当a>1，b>1时，显然ab>1，D正确．‎ 答案　D ‎6．命题p：∀x∈R，ax2＋ax＋1≥0，若綈p是真命题，则实数a的取值范围是(　　)‎ A．(0，4]‎ B．[0，4]‎ C．(－∞，0]∪[4，＋∞)‎ D．(－∞，0)∪(4，＋∞)‎ 解析　因为命题p：∀x∈R，ax2＋ax＋1≥0，‎ 所以命题綈p：∃x∈R，ax2＋ax＋1<0，‎ 则a<0或解得a<0或a>4.‎ 答案　D ‎7．已知命题p：∃α∈R，cos(π－α)＝cos α；命题q：∀x∈R，x2＋1>0.则下面结论正确的是(　　)‎ A．p∧q是真命题 B．p∧q是假命题 C．綈p是真命题 D．綈q是真命题 解析　对于p：取α＝，则cos(π－α)＝cos α，‎ 所以命题p为真命题；‎ 对于命题q：∵x2≥0，∴x2＋1>0，所以q为真命题．由此可得p∧q是真命题．‎ 答案　A ‎8．已知命题p：∃x∈R，(m＋1)(x2＋1)≤0，命题q：∀x∈R，x2＋mx＋1>0恒成立．若p∧q 为假命题，则实数m的取值范围为(　　)‎ A．[2，＋∞)‎ B．(－∞，－2]∪(－1，＋∞)‎ C．(－∞，－2]∪[2，＋∞)‎ D．(－1，2]‎ ‎9．已知命题p：∀x∈R，x＋≥2；命题q：∃x∈(0，＋∞)，x2＞x3，则下列命题中为真命题的是(　　)‎ A．(綈p)∧q B．p∧(綈q) C．(綈p)∧(綈q) D．p∧q 解析　对于p：当x＝－1时，x＋＝－2，∴p为假命题．取x0∈(0，1)，此时x＞x，∴q为真命题．‎ 从而綈p为真命题，(綈p)∧q为真命题．‎ 答案　A ‎10．命题“∃x∈，tan x>sin x”的否定是________．‎ 答案　∀x∈，tan x≤sin x ‎11．若命题“∃x∈R，使得x2＋(a－1)x＋1＜0”是真命题，则实数a的取值范围是________．‎ 解析　∵“∃x∈R，使得x2＋(a－1)x＋1＜0”是真命题，‎ ‎∴Δ＝(a－1)2－4＞0，即(a－1)2＞4，‎ ‎∴a－1＞2或a－1＜－2，‎ ‎∴a＞3或a＜－1.‎ 答案　(－∞，－1)∪(3，＋∞)‎ ‎12．已知下列四个命题：‎ ‎①“若x2－x＝0，则x＝0或x＝1”的逆否命题为“x≠0且x≠1，则x2－x≠0”‎ ‎②“x<1”是“x2－3x＋2>0”的充分不必要条件 ‎③命题p：存在x∈R，使得x2＋x＋1<0，则綈p：任意x∈R，都有x2＋x＋1≥0‎ ‎④若p∧q为假命题，则p，q均为假命题 其中真命题的是________(填序号)．‎ ‎13．已知命题p：“∀x∈[0，1]，a≥ex”；命题q：“∃x∈R，使得x2＋4x＋a＝0”．若命题“p∧q”是真命题，则实数a的取值范围是________．‎ 解析　若命题“p∧q”是真命题，那么命题p，q都是真命题．由∀x∈[0，1]，a≥ex，得a≥e；由∃x∈R，使x2＋4x＋a＝0，知Δ＝16－4a≥0，得a≤4，因此e≤a≤4.‎ 答案　[e，4]‎ ‎14．下列四个说法：‎ ‎①一个命题的逆命题为真，则它的逆否命题一定为真；‎ ‎②命题“设a，b∈R，若a＋b≠6，则a≠3或b≠3”是一个假命题；‎ ‎③“x>2”是“<”的充分不必要条件；‎ ‎④一个命题的否命题为真，则它的逆命题一定为真．‎ 其中说法不正确的序号是________．‎ ‎15．已知命题p：∃x∈R，ex－mx＝0，q：∀x∈R，x2－2mx＋1≥0，若p∨(綈q)为假命题，则实数m的取值范围是________． ‎ 解析　若p∨(綈q)为假命题，则p假q真．‎ 由ex－mx＝0得m＝，设f(x)＝，‎ 则f′(x)＝＝.‎ 当x＞1时，f′(x)＞0，此时函数单调递增；‎ 当0＜x＜1时，f′(x)＜0，此时函数单调递减；‎ 当x＜0时，f′(x)＜0，此时函数单调递减．‎ 由f(x)的图象及单调性知当x＝1时，f(x)＝取得极小值f(1)＝e，所以函数f(x)＝的值域为 ‎(－∞，0)∪[e，＋∞)，所以若p是假命题，则0≤m＜e；‎ 命题q为真命题时，有Δ＝4m2－4≤0，则－1≤m≤1.‎ 所以当p∨(綈q)为假命题时，m的取值范围是[0，1]．‎ 答案　[0，1]‎