2018届二轮复习命题及简要逻辑课件（全国通用）

2018届二轮复习命题及简要逻辑课件（全国通用）

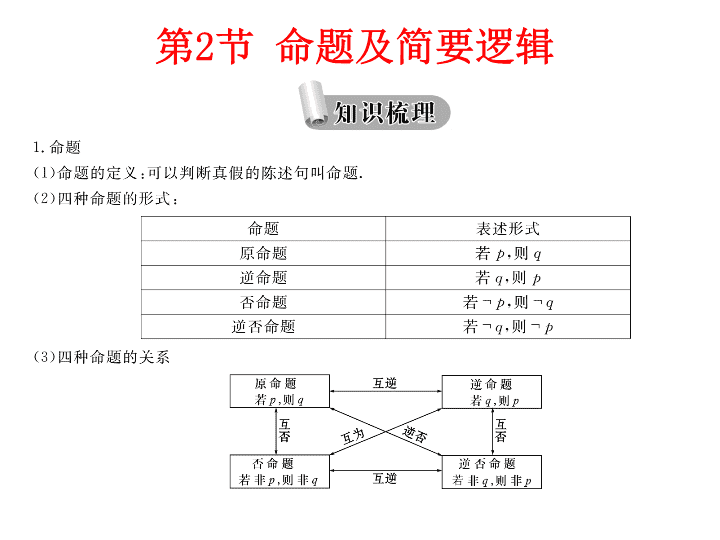
第一章　集合、逻辑联结词、 复数、程序框图 第 2 节 命题及简要逻辑 【 答案 】 B 【 解析 】 对于① , 若 p ∨ q 为真命题 , 则 p , q 至少有一个为真 , 即可能有一个为假 , 所以 p ∧ q 不一定为真命题 , 所以①错误 ; 对于② , 由 x 2 - 4 x- 5>0 可得 x> 5 或 x<- 1, 所以“ x >5” 是“ x 2 - 4 x- 5>0” 的充分不必要条件 , 所以②正确 ; 对于③ , 根据特称命题的否定为全称命题 , 可知③正确 ; 对于④ , 命题“若 x 2 - 3 x+ 2 = 0, 则 x= 1 或 x= 2” 的逆否命题为“若 x ≠1 且 x ≠2, 则 x 2 - 3 x+ 2≠0”, 所以④错误 , 所以错误命题的个数为 2, 故选 B . 1 . 命题“若一个数是负数 , 则它的平方是正数”的逆命题是 ( ) A.“ 若一个数是负数 , 则它的平方不是正数” B.“ 若一个数的平方是正数 , 则它是负数” C.“ 若一个数不是负数 , 则它的平方不是正数” D.“ 若一个数的平方不是正数 , 则它不是负数” 【 答案 】 B 【 解析 】 因为 p ⇒ q 的逆命题为 q ⇒ p , 所以“若一个数是负数 , 则它的平方是正数”的逆命题为“若一个数的平方是正数 , 则它是负数” . 选 B . 3 . 命题“若 x 2 <1, 则 - 1< x <1” 的逆否命题是 ( ) A . 若 x 2 ≥1, 则 x ≥1 且 x ≤ - 1 B . 若 - 1< x <1, 则 x 2 <1 C . 若 x >1 或 x < - 1, 则 x 2 >1 D. 若 x ≥1 或 x ≤ - 1, 则 x 2 ≥1 【 答案 】 D 【 解析 】 p ⇒ q 的逆否命题为 ¬ q ⇒¬ p , 所以“若 x 2 <1, 则 - 1< x <1” 的逆否命题是“若 x ≥1 或 x ≤ - 1, 则 x 2 ≥1” . 选 D . 4 . 若 p 是真命题 , q 是假命题 , 则 ( ) A. p ∧ q 是真命题 B. p ∨ q 是假命题 C.¬ p 是真命题 D.¬ q 是真命题 【 答案 】 D 【 解析 】 q 是假命题 , 则 ¬ q 是真命题 . 选 D . 5 . 若 ¬ p ∨ q 是假命题 , 则 ( ) A. p ∧ q 是假命题 B. p ∨ q 是假命题 C. p 是假命题 D.¬ q 是假命题 【 答案 】 A 【 解析 】 若 ¬ p ∨ q 是假命题 , 则 p 是真命题 , q 是假命题 . 所以 p ∧ q 是假命题 . 选 A . 6 . 命题“∃ x ∈ R , x 2 +4 x +5≤0” 的否定是 ( ) A.∃ x ∈ R , x 2 +4 x +5>0 B.∃ x ∈ R , x 2 +4 x +5≤0 C.∀ x ∈ R , x 2 +4 x +5>0 D.∀ x ∈ R , x 2 +4 x +5≤0 【 答案 】 C 【 解析 】 命题“∃ x ∈ R , x 2 +4 x +5≤0” 的否定是“∀ x ∈ R , x 2 +4 x +5>0” . 7 . 下列说法中正确的有 ( ) ① 命题“若 x 2 - 3 x +2 = 0, 则 x= 1” 的逆否命题为“若 x ≠1, 则 x 2 - 3 x +2≠0”; ②“ x >2” 是“ x 2 - 3 x +2>0” 的充分不必要条件 ; ③ 若 p ∧ q 为假命题 , 则 p 、 q 均为假命题 ; ④ 对于命题 p :∃ x ∈R, x 2 + x +1 < 0, 则� p :∀ x ∈R, x 2 + x +1≥0 . A.1 个 B.2 个 C.3 个 D.4 个 【 答案 】 C 【 解析 】 ① 符合逆否命题的定义 ,① 对 ; ② x 2 - 3 x +2>0 时得到 x <1 或 x >2, 所以 x >2 时有 x 2 - 3 x +2>0 , 反之不成立 , 所以②对 ; ③ 若 p ∧ q 为假命题 , 可以是 p 真命题 , q 为假命题 , 所以③错 ; ④ 符合特称命题的否命题的定义 ,④ 对 ; 所以①②④对 . 选 C . 8 . (2017 山东高考卷 ) 已知命题 p :∀ x >0,ln( x +1)>0; 命题 q : 若 a>b , 则 a 2 >b 2 , 下列命题为真命题的是 ( ) A. p ∧ q B. p ∧¬ q C.¬ p ∧ q D.¬ p ∧¬ q 【 答案 】 B 【 解析 】 由 x >0 时 x +1>1,ln( x +1) > 0, 知 p 是真命题 , 由 - 1> - 2, 但 ( - 1) 2 <( - 2) 2 可知 q 是假命题 , 即 p ,¬ q 均是真命题 , 故选 B . 9. (2015 山东 ) 若“∀ x ∈[0, ],tan x ≤ m ” 是真命题 , 则实数 m 的最小值为 . 【答案】 1 【解析】 “∀ x ∈[0, ],tan x ≤ m ”是真命题,则 m ≥tan =1,于是实数 m 的最小值为1 . 10 . 设 a , b 是向量 , 命题“若 a = -b , 则 | a |=| b |” 的逆命题是 ( ) A. 若 a ≠ -b , 则 | a |≠| b | B. 若 a = -b , 则 | a |≠| b | C. 若 | a |≠| b |, 则 a ≠ -b D. 若 | a |=| b |, 则 a = -b 【 答案 】 D 【 解析 】 因为逆命题是以原命题的结论为条件 , 条件为结论的命题 , 所以这个命题的逆命题为“若 | a |=| b |, 则 a = -b ” . 11 . 命题“若 p 则 q ” 的逆命题是 ( ) A. 若 q 则 p B. 若 ¬ p 则 ¬ q C. 若 ¬ q 则 ¬ p D. 若 p 则 ¬ q 【 答案 】 A 【 解析 】 “ 若 p 则 q ” 的逆命题是 : 若 q 则 p. 故 A 正确 . 12 . 已知命题 p : 对任意 x ∈R, 总有 | x |≥0; q : x =1 是方程 x +2=0 的根 , 则下列命题为真命题的是 ( ) A. p ∧¬ q B.¬ p ∧ q C.¬ p ∧¬ q D. p ∧ q 【 答案 】 A 【 解析 】 因为命题 p 为真 , 命题 q 为假命题 , 所以 A 选项正确 . 13 . 命题“存在实数 x , 使 x >1” 的否定是 ( ) A. 对任意实数 x , 都有 x >1 B. 不存在实数 x , 使 x ≤1 C. 对任意实数 x , 都有 x ≤1 D. 存在实数 x , 使 x ≤1 【 答案 】 C 【 解析 】 存在 —— 任意 , x >1—— x ≤1 . 14 . 与命题“若 a ∈ M , 则 b ∉ M ” 等价的命题是 ( ) A. 若 a ∉ M , 则 b ∉ M B. 若 b ∉ M , 则 a ∈ M C. 若 a ∉ M , 则 b ∈ M D. 若 b ∈ M , 则 a ∉ M 【 答案 】 D 【 解析 】 因为原命题只与逆否命题是等价命题 , 所以只需写出原命题的逆否命题即可 .