- 2021-06-24 发布 |
- 37.5 KB |
- 8页

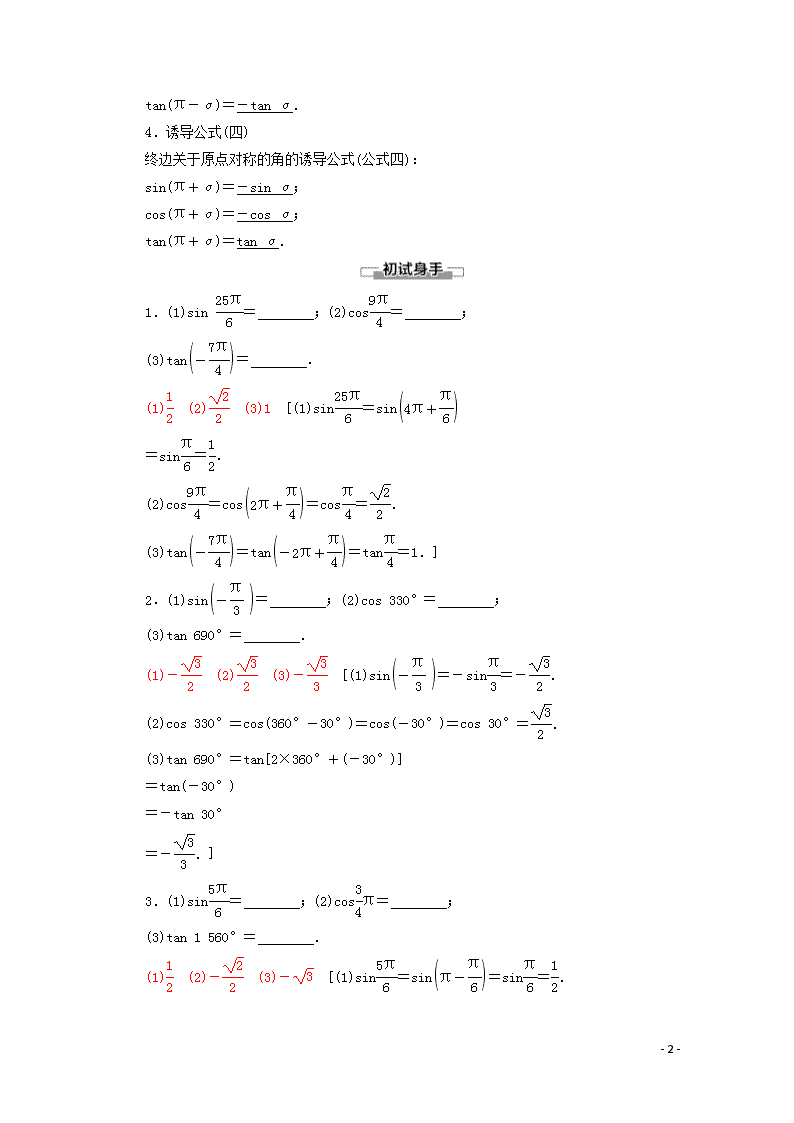

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020_2021学年新教材高中数学第7章三角函数7
7.2.3 三角函数的诱导公式 第1课时 三角函数的诱导公式(一~四) 学 习 目 标 核 心 素 养 1.能借助单位圆中的三角函数定义推导出诱导公式一~四.(难点) 2.掌握诱导公式一~四,会运用诱导公式化简、求值与证明.(重点) 通过学习本节内容,提升学生的数学运算核心素养. 结合单位圆,思考:与角α终边相同的角的表示形式是什么?它们的三角函数值之间具有怎样的关系?与角α的终边关于x轴对称的角表示形式是什么?它们的三角函数值之间具有怎样的关系? 1.诱导公式(一) 终边相同的角的诱导公式(公式一): sin(α+2kπ)=sin α(k∈Z); cos(α+2kπ)=cos α(k∈Z); tan(α+2kπ)=tan α(k∈Z). 思考1:终边相同的角的同一三角函数值之间有什么关系? [提示] 相等. 2.诱导公式(二) 终边关于x轴对称的角的诱导公式(公式二): sin(-α)=-sin α; cos(-α)=cos α; tan(-α)=-tan α. 思考2:角-α的终边与单位圆的交点与角α的终边与单位圆的交点有何关系? [提示] 关于x轴对称. 3.诱导公式(三) 终边关于y轴对称的角的诱导公式(公式三): sin(π-α)=sin α; cos(π-α)=-cos α; - 8 - tan(π-α)=-tan α. 4.诱导公式(四) 终边关于原点对称的角的诱导公式(公式四): sin(π+α)=-sin α; cos(π+α)=-cos α; tan(π+α)=tan α. 1.(1)sin = ;(2)cos= ; (3)tan= . (1) (2) (3)1 [(1)sin=sin =sin=. (2)cos=cos=cos=. (3)tan=tan=tan=1.] 2.(1)sin= ;(2)cos 330°= ; (3)tan 690°= . (1)- (2) (3)- [(1)sin=-sin=-. (2)cos 330°=cos(360°-30°)=cos(-30°)=cos 30°=. (3)tan 690°=tan[2×360°+(-30°)] =tan(-30°) =-tan 30° =-.] 3.(1)sin= ;(2)cosπ= ; (3)tan 1 560°= . (1) (2)- (3)- [(1)sin=sin=sin=. (2)cos=cos=-cos=-. - 8 - (3)tan 1 560°=tan(4×360°+120°)=tan 120°=tan(180°-60°)=-tan 60°=-.] 4.(1)sin 225°= ;(2)cos= ; (3)tan = . (1)- (2)- (3) [(1)sin 225°=sin(180°+45°)=-sin 45°=-. (2)cos=cos=-cos=-. (3)tan=tan =tan=tan=.] 给角求值 【例1】 求下列各三角函数式的值: (1)sin(-660°);(2)cos ;(3)2cos 660°+sin 630°; (4)tan ·sin. [思路点拨] 利用诱导公式先把任意角的三角函数化为三角函数,再求值. [解] (1)因为-660°=-2×360°+60°, 所以sin(-660°)=sin 60°=. (2)因为=6π+,所以cos =cos =-. (3)原式=2cos(720°-60°)+sin(720°-90°) =2cos 60°-sin 90°=2×-1=0. (4)tan ·sin =tan·sin - 8 - =tan ·sin =×=. 利用诱导公式求任意角的三角函数值的步骤 1.求下列各三角函数式的值: (1)sin 1 320°;(2)cos;(3)tan(-945°). [解] (1)sin 1 320°=sin(4×360°-120°) =sin(-120°)=-sin(180°-60°) =-sin 60°=-. (2)cos=cos=cos =-cos=-. (3)tan(-945°)=-tan 945° =-tan(225°+2×360°)=-tan 225° =-tan(180°+45°)=-tan 45°=-1. 化简求值 【例2】 化简:(1); (2). [思路点拨] 利用诱导公式一,二,三,四将函数值化为角α的三角函数值或锐角的三角函数值,再约分化简. [解] (1)====1. - 8 - (2)原式= ===-1. 三角函数式的化简方法 (1)利用诱导公式,将任意角的三角函数转化为锐角的三角函数. (2)常用“切化弦”法,即表达式中的切函数通常化为弦函数. (3)注意“1”的变式应用:如1=sin2α+cos2α=tan . 2.(k∈Z). [解] 当k=2n(n∈Z)时, 原式= = ==-1; 当k=2n+1(n∈Z)时, 原式= == =-1. 综上,原式=-1. 给值求值问题 [探究问题] 1.“α-15°”与“165°+α”间存在怎样的关系?你能用“α-15°”表示“165°+α”吗? [提示] 由165°+α-(α-15°)=180°可知165°+α=180°+(α-15°). 2.若tan(α-15°)=-1,则tan(165°+α)等于多少? [提示] 由探究1可知tan(165°+α)=tan[180°+(α-15°)]=tan(α-15°)=-1. 【例3】 求值. - 8 - (1)已知sin=-,求sin的值; (2)已知cos=,求cos的值. [思路点拨] (1)-=2π; (2)-=π. [解] (1)∵-=2π, ∴sin=sin =sin=-. (2)∵-=π, ∴cos=cos =-cos=-. 1.(变条件)本例(1)条件变为“已知sin=”,求sin的值. [解] ∵-=6π, ∴sin=sin =sin=. 2.(变结论)本例(2)已知条件不变,求cos的值. [解] ∵-=-π, ∴cos=cos =cos =-cos=-. - 8 - 对于给值求值问题,要注意观察题目条件中的角与所求问题中的角之间的联系,然后选择恰当的诱导公式进行转化,一般采用代入法求值. 提醒:设法消除已知式与所求式之间的种种差异是解决问题的关键. 3.已知sin(α-360°)-cos(180°-α)=m,则sin(180°+α)·cos(180°-α)等于( ) A. B. C. D.- A [∵sin(α-360°)-cos(180°-α)=sin α+cos α=m, ∴sin(180°+α)cos(180°-α)=sin αcos α==.故选A.] 4.已知cos(α-75°)=-,且α为第四象限角,求sin(105°+α)的值. [解] ∵cos(α-75°)=-<0,且α为第四象限角, ∴sin(α-75°)=-=-=-, ∴sin(105°+α)=sin[180°+(α-75°)]=-sin(α-75°)=. 1.明确各诱导公式的作用 诱导公式 作用 公式一 将角转化为0~2π之间的角求值 公式二 将负角转化为正角求值 公式三 将角转化为0~之间的角求值 公式四 将角转化为0~之间的角求值 2.诱导公式的记忆 - 8 - 这四组诱导公式的记忆口诀是“函数名不变,符号看象限”.其含义是诱导公式两边的函数名称一致,符号则是将α看成锐角时原角所在象限的三角函数值的符号.α看成锐角,只是公式记忆的方便,实际上α可以是任意角. 1.已知sin(θ+π)<0,cos(θ-π)>0,则角θ的终边落在( ) A.第一象限 B.第二象限 C.第三角限 D.第四象限 B [由sin(θ+π)=-sin θ<0⇒sin θ>0,cos(θ-π)=-cos θ>0⇒cos θ<0,由可知θ是第二象限角.] 2.tan 255°=( ) A.-2- B.-2+ C.2- D.2+ [答案] D 3.代数式sin 120°cos 210°的值为 . - [由诱导公式可得,sin 120°cos 210°=sin 60°×(-cos 30°)=×=-.] 4.已知sin(π+α)=,且α是第四象限角,求cos(α-2π)的值. [解] ∵sin(π+α)=,∴sin α=-, 又α是第四象限角, ∴cos α===, ∴cos(α-2π)=cos α=. - 8 -查看更多