2020届二轮复习基本计数原理的综合应用教案（全国通用）

2020届二轮复习基本计数原理的综合应用教案（全国通用）

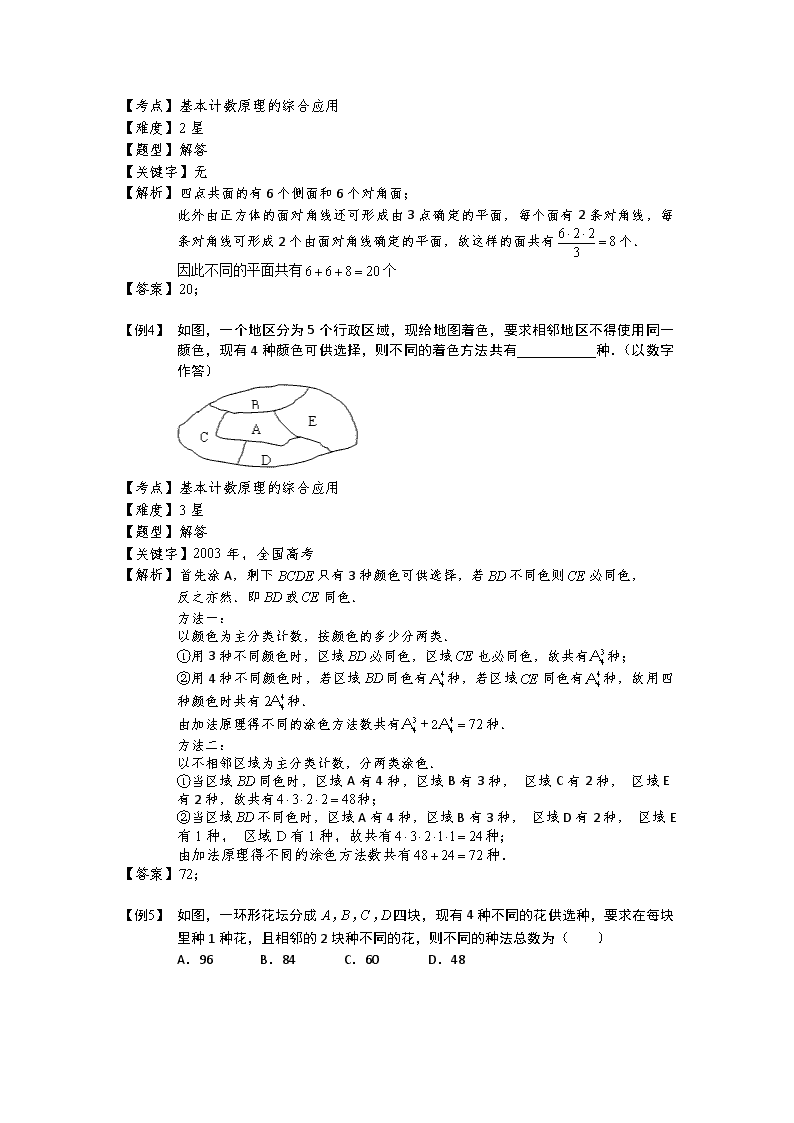
基本计数原理的综合应用 【例 1】 用 0 ， 3， 4 ， 5 ， 6 排成无重复字的五位数，要求偶数字相邻，奇数字也相邻， 则这样的五位数的个数是_________．（用数字作答） 【考点】基本计数原理的综合应用 【难度】2 星 【题型】填空 【关键字】无 【解析】略 【答案】20； 【例 2】 若自然数 n 使得作竖式加法 ( 1) ( 2)n n n    均不产生进位现象．则称 n 为“可连 数”．例如：32 是“可连数”，因 32 33 34  不产生进位现象；23 不是“可连数”，因 23 24 25  产生进位现象．那么，小于1000 的“可连数”的个数为（ ） A． 27 B． 36 C． 39 D． 48 【考点】基本计数原理的综合应用 【难度】3 星 【题型】选择 【关键字】无 【解析】“可连数”是一位数时，设为 a ，则 ( 1) ( 2) 3 3 10 2a a a a a        ≤ ， 共有 3个； 是两位数时，设为 ab ，易知 8 9b  ， ， ( 1) ( 2) (3 )(3 3)ab a b a b a b      ，由题意 3 10 0a a ， ，且 3 3 10 2b b   ≤ ， 1 2 3a  ， ， ， 0 1 2b  ，， ，共有 3 3 9  个； 是三位数时，设为 abc ，易知 8 9c  ， ， ( 1) ( 2) (3 )(3 )(3 3)abc ab c ab c a b c      ， 由题意有 3 10a  0a  ， 3 10b  ， 3 3 10c   ，故 1 2 3a  ， ， ， 0 1 2 3b  ，， ， ， 0 1 2c  ，， ，共有 3 4 3 36   个． 可连数的个数为3 9 36 48   个．选 D． 【答案】D； 【例 3】 由正方体的 8 个顶点可确定多少个不同的平面？ 典例分析 基本计数原理的综合应用 【考点】基本计数原理的综合应用 【难度】2 星 【题型】解答 【关键字】无 【解析】四点共面的有 6 个侧面和 6 个对角面； 此外由正方体的面对角线还可形成由 3 点确定的平面，每个面有 2 条对角线，每 条对角线可形成 2 个由面对角线确定的平面，故这样的面共有 6 2 2 83    个． 因此不同的平面共有 6 6 8 20   个 【答案】20； 【例 4】 如图，一个地区分为 5 个行政区域，现给地图着色，要求相邻地区不得使用同一 颜色，现有 4 种颜色可供选择，则不同的着色方法共有 种．（以数字 作答） 【考点】基本计数原理的综合应用 【难度】3 星 【题型】解答 【关键字】2003 年，全国高考 【解析】首先涂 A，剩下 BCDE 只有 3 种颜色可供选择，若 BD 不同色则 CE 必同色， 反之亦然．即 BD 或 CE 同色． 方法一： 以颜色为主分类计数，按颜色的多少分两类． ①用 3 种不同颜色时，区域 BD 必同色，区域 CE 也必同色，故共有 3 4Α 种； ②用 4 种不同颜色时，若区域 BD 同色有 4 4Α 种，若区域 CE 同色有 4 4Α 种，故用四 种颜色时共有 4 42Α 种． 由加法原理得不同的涂色方法数共有 3 4 4 4 72Α + 2Α 种． 方法二： 以不相邻区域为主分类计数，分两类涂色． ①当区域 BD 同色时，区域 A 有 4 种，区域 B 有 3 种， 区域 C 有 2 种， 区域 E 有 2 种，故共有 4 3 2 2 48    种； ②当区域 BD 不同色时，区域 A 有 4 种，区域 B 有 3 种， 区域 D 有 2 种， 区域 E 有 1 种， 区域 D 有 1 种，故共有 4 3 2 1 1 24     种； 由加法原理得不同的涂色方法数共有 48 24 72  种． 【答案】72； 【例 5】 如图，一环形花坛分成 A B C D， ， ， 四块，现有 4 种不同的花供选种，要求在每块 里种 1 种花，且相邻的 2 块种不同的花，则不同的种法总数为（ ） A．96 B．84 C．60 D．48 【考点】基本计数原理的综合应用 【难度】3 星 【题型】选择 【关键字】2018 年，全国高考 【解析】相当于四种颜色涂 A B C D， ， ， ，相邻的不同色． 方法一： 以颜色为主分类计数，按颜色的多少分三类． ①用 4 种颜色时，有 4 4Α 种； ②用 3 种颜色时，则 AC 同色或 BD 同色，分别都有 3 4Α 种； ③用 2 种颜色时，则 AC 同色且 BD 同色，有 2 4Α 种 总共有 4 4Α +2 3 4Α + 2 4Α 84 种，选 B 方法二： 以不相邻区域为主分类计数 首先 A 有 4 种可选． 当 BD 同色时，B 有 3 种，C 有 3 种； 当 BD 不同色时，B 有 3 种，D 有 2 种，C 有 2 种． 由加法和乘法原理可得总数为 4 3 3 4 3 2 2 84       种． 【答案】B; 【例 6】 某城市在中心广场建造一个花圃，花圃分为 6 个部分（如图）．现要栽种 4 种不同 颜色的花，每部分栽种一种且相邻部分不能栽种同样颜色的花，不同的栽种方法有 种．（以数字作答） 【考点】基本计数原理的综合应用 【难度】4 星 【题型】填空 【关键字】2003 年，江苏高考 【解析】方法一： 以区域为主分步计数（从相邻颜色最多的区域开始（最大相邻原则）），分 4 步涂色， 第一步先涂 1 有 4 种，第二步再涂 2（与 1 不同色）有 3 种，第三步涂 3（与 1、 2 不同色）有 2 种． 4 和 6 都有 2 种，其中 4 和 6 同色的有 1 种，不同色的有 3 种．同色时，5 有 2 种； 不同色时，5 只有 1 种．故总共有 4 3 2 (1 2 3 1) 120       种． 方法二： 以颜色为主分步计数，易知 4 种颜色都得用到（格 1 与其它的都不同色，而涂剩 下的格子两种颜色显然不够）． ①先涂 1，有 4 种； ②剩下 3 种颜色涂剩下 5 个格子，必有一种颜色只在一个格子出现，从剩余 5 个 格子中选一个涂这种颜色有 3· 1 5C =15 种； ③剩余 4 个格子用剩余的两种颜色染只有 2 种染法，由乘法原理共有 4·15·2=120 种． 方法三： 用分类思想解决． 易知 4 种颜色都得用到，而且没有一种颜色会涂 3 个格子，最多涂两个．因此 4 种颜色涂 6 个格子的方案只能是：两种颜色各涂一个格子，另两种要各涂两个格子． ①2 与 5 同色、4 与 6 同色，则有 4 4Α ； ②3 与 5 同色、4 与 6 同色，则有 4 4Α ； ③2 与 5 同色、3 与 6 同色，则有 4 4Α ； ④3 与 5 同色、2 与 4 同色，则有 4 4Α ； ⑤2 与 4 同色、3 与 6 同色，则有 4 4Α ； 所以根据加法原理得涂色方法总数为 4 4 1205Α ． 【答案】120； 【例 7】 分母是 385 的最简真分数一共有多少个？并求它们的和． 【考点】基本计数原理的综合应用 【难度】4 星 【题型】解答 【关键字】无 【解析】385 5 7 11   ，实际上就是找分子中不能被 5 或 7 或 11 整除的数个数，用间接法． ⑴被 5、7 和 11 这 3 个都整除的只有 385 一个； ⑵只被其中两个整除的：只被 5 和 7 整除的有 385 1 1035   个；只被 5 和 11 整除的 有 385 1 655   个；只被 7 和 11 整除的有 385 1 477   个．共有10 6 4 20   个； ⑶只被其中 1 个整除的：能被 5 整除的共有 385 775  个，其中包括只被 5 和 7 整 除的 10 个、只被 5 和 11 整除的 6 个以及被 3 个整除的 1 个，故只能被 5 整除的 有 77 10 6 1 60    个；同样的可算出只能被 7 整除的有55 10 4 1 40    个；只 能被 11 整除的有 35 6 4 1 24    个．共有 60 40 24 124   个． 因此 1 到 385 中不能被 5 或 7 或 11 整除的数有 385 1 20 124 240    个，即最简 真分数有 240 个． 如果有一个最简真分数为 385 a ，则必有一个最简真分数为 385 385 a 与之对应，这 一对的和为 1．因此 240 个最简真分数的和为 240 1202  ． 【答案】120； 【例 8】 某人有 4 种颜色的灯泡（每种颜色的灯泡足够多），要在如图所示的 6 个点 A、B、 C、A1、B1、C1 上各装一个灯泡，要求同一条线段两端的灯泡不同色，则每种颜色的 灯泡都至少用一个的安装方法共有 种（用数字作答） 【考点】基本计数原理的综合应用 【难度】4 星 【题型】填空 【关键字】2018 年，重庆高考 【解析】同样可看成对 6 个点进行 4 种颜色的涂色，同一线段两端不同色， 每种颜色至少有一种． 首先对 A 涂色，共有 4 种可能，然后 B 有 3 种，C 有 2 种， ABC 已经用了 3 种颜 色，因为每种颜色都至少有一个，所以 当 1A 涂第 4 种颜色时， 1B 有两种颜色可选择（A 或 C 的颜色） ① 1B 与 A 同色，此时 1C 只能选 B 的颜色，只有 1 种； ② 1B 与 C 同色，此时 1C 有 2 种选择（A 或 B 的颜色） 故共有 4 3 2 (1 2) 72     种方法． 同样的，当 1B 或 1C 涂第 4 种颜色时，也各有 72 种 因此总方法数是 72 3 216  ． 【答案】216； 【例 9】 用 0 ，1，2 ，3，4 ，5 这 6 个数字，可以组成_______个大于3000 ，小于5421 的 数字不重复的四位数． 【考点】基本计数原理的综合应用 【难度】3 星 【题型】填空 【关键字】无 【解析】分四类： ①千位数字为 3 , 4 之一时，百十个位数只要不重复即可，有 2 5 4 3 120    （个）； ②千位数字为 5 ，百位数字为 0 ,1, 2 , 3 之一时，共有1 4 4 3 48    （个）； ③千位数字是 5 ，百位数字是 4 ，十位数字是 0 ,1之一时，共有1 1 2 3 6    （个）； ④最后还有 5420 也满足条件． 所以所求四位数共有120 48 6 1 175    （个）． 【答案】175； 【例 10】 某 通 讯 公 司 推 出 一 组 手 机 卡 号 码 ， 卡 号 的 前 七 位 数 字 固 定 ， 从 “ 0000 ”到“ 9999 ”共10000 个号码．公司规定：凡卡号的后四位 带有数字“ 4 ”或“ 7 ”的一律作为“优惠卡”，则这组号码中“优惠卡”的个数为（ ） A． 2000 B． 4096 C． 5904 D．8320 【考点】基本计数原理的综合应用 【难度】3 星 【题型】选择 【关键字】2018 年，福建高考 【解析】先考虑所有的号码数：后四位依次选择数字，分成四步，每步有10 种选法， 共 410 种选取方法；再考虑后四位都不带有 4 和 7 的所有号码，每步有8种选法， 仍然是 4 步，共有 48 种选法，故“优惠卡”的个数为 4 410 8 5904  （个）． 【答案】C； 【例 11】 同室 4 人各写1张贺年卡，先集中起来，然后每人从中各拿1张别人送出的贺 年卡，则 4 张贺年卡不同的分配方式有（ ） A． 6 种 B． 9 种 C．11 种 D． 23 种 【考点】基本计数原理的综合应用 【难度】3 星 【题型】选择 【关键字】无 【解析】略分析：本题完成的具体事情是四个人，每人抽取一张贺卡， 问题是按照一定要求，抽取结果有多少种不同情况．我们可以把抽卡片的过程分成 四步，先是第一人抽，然后第二人，以此类推，但存在的问题是，我们把四个人记 为 A 、 B 、 C 、 D ，他们的卡片依次记为 a 、 b 、 c 、 d ，如果第一步 A 抽取 b ， 接着 B 可抽 a 、 c 、 d ，有三种方法，而 A 抽 c 或 d ， B 仅有两种抽法，这样两步 之间产生影响，这样必须就 A 抽的结果进行分类． 法一： 设四人 A 、B 、C 、D 写的贺年卡分别是 a 、b 、c 、d ，当 A 拿贺年卡b ，则 B 可拿 a 、c 、 d 中的任何一个，即“ B 拿 a ，C 拿 d ， D 拿c ”或“ B 拿 c ， D 拿 a ， C 拿 d ”或“ B 拿 d ，C 拿 a ， D 拿 c ”，所以 A 拿 b 时有三种不同分配方 法．同理， A 拿 c 、 d 时也各有三种不同的分配方式．由分类计数原理，四张 贺年卡共有3 3 3 9   种分配方式． 法二： 让四人 A 、 B 、C 、 D 依次拿一张别人送出的贺年卡．如果 A 先拿有3种，此 时写被 A 拿走的那张贺年卡的人也有 3种不同的取法．接下来，剩下的两个人 都各只有一种取法．由分步计数原理，四张贺年卡不同的分配方式有 3 3 1 1 9    种． ∴ 应选 B． 点评：⑴本题从不同的角度去思考，从而得到不同的解答方法，法一是用分类 计数原理解答的，法二是用分步计数原理解答的． ⑵如果把四个人依次抽取的结果用一个图表体现出来，就显得更加清楚． 共有9 种不同结果． 这个图表我们称之为“树形图”，在解决此类问题往往很有效，通过它可以把各 种不同结果直观地表现出来． 【答案】B； 【例 12】 某班新年联欢会原定的 6 个节目已排成节目单，开演前又增加了 3 个新节目， 如果将这 3 个节目插入原节目单中，那么不同的插法种数为（ ） A．504 B． 210 C． 336 D．120 【考点】基本计数原理的综合应用 【难度】2 星 【题型】选择 【关键字】无 【解析】略 【答案】A； 【例 13】 某班学生参加植树节活动，苗圃中有甲、乙、丙 3 种不同的树苗，从中取出 5 棵分别种植在排成一排的 5 个树坑内，同种树苗不能相邻，且第一个树坑和第 5 个树坑只能种甲种树苗的种法共（ ） A．15 种 B．12 种 C．9 种 D．6 种 【考点】基本计数原理的综合应用 【难度】2 星 【题型】选择 【关键字】2018 年，北京崇文一模 【解析】按第三个树坑分类， 如果种甲种树苗，则有 2 2 4  种方案； 如果种乙或丙种树苗，都只有1种方案； 因此总共的方案有 4 1 1 6   种。D; 【答案】D； 【例 14】 如图所示，画中的一朵花，有五片花瓣.现有四种不同颜色的画笔可供选择， 规定每片花瓣都要涂色，且只涂一种颜色.若涂完的花中颜色相同的花瓣恰有三片， 则不同涂法种数为 （用数字作答）. 【考点】基本计数原理的综合应用 【难度】3 星 【题型】填空 【关键字】2018 年，海淀一模 【解析】先从五片花瓣中取三片，有 3 5C 种取法，再从 4 种颜色选一种涂色， 最后再涂其余两片花瓣，因此共有 3 1 2 5 4 3 10 4 6 240   C C A 种不同的涂法. 【答案】240； 【例 15】 用 0 到 9 这10 个数字，可以组成没有重复数字的三位偶数的个数为（ ） A．324 B． 328 C．360 D． 648 【考点】基本计数原理的综合应用 【难度】2 星 【题型】选择 【关键字】2009 年，北京高考 【解析】分两种情况：个数为 0 与个位不为 0 ． 个位为 0 的数只需再确定十位与百位即可，有 9 8 72  个；个位不为 0 的，需 要在 2 4 6 8， ， ， 中任选一个放在个位，再在除 0 与个位数字之外的8个数字中选 择一个数字放在百位，最后选定十位，共有 4 8 8 256   种．故共有满足条件 的数 72 256 328  个． 【答案】B； 【例 16】 用红、黄、蓝三种颜色之一去涂图中标号为1 2 9， ， ， 的 9 个小正方形（如图）， 使得任意相邻（有公共边的）小正方形所涂颜色都不相同，且“ 3、 5 、 7 ”号数字 涂相同的颜色，则符合条件的所有涂法共有（ ）种． 9 8 7 6 5 4 3 2 1 A． 72 B．108 C．144 D．192 【考点】基本计数原理的综合应用 【难度】3 星 【题型】选择 【关键字】无 【解析】B．涂 3 5 7， ， 标记的小正方形，有 3种方案； 涂1中的小正方形，若涂的颜色与3 5 7， ， 中的颜色相同，则涂 2, 4 有 2 2 4  种方 案； 若涂的颜色与 3 5 7， ， 中的颜色不同，有 2 种涂法，则涂 2, 4 有1种方案； 于是总的涂法为 23 (4 2) 108   种． 【答案】B; 【例 17】 足球比赛的计分规则是：胜一场得 3 分，平一场得 1 分，负一场得 0 分，那么 一个队打 14 场共得 19 分的情况有（ ） A．3种 B． 4 种 C．5 种 D． 6 种 【考点】基本计数原理的综合应用 【难度】3 星 【题型】选择 【关键字】无 【解析】设胜、平、负的场次分别为 x y z， ， ，则 14 19 3 3 19 2 5 x y z y x x y z x            ， 由 0 0y z≥ ， ≥ ，可得3 6x≤ ≤ ，即可得所求情况有 4 种． 【答案】B