2018届二轮复习古典概型

2018届二轮复习古典概型

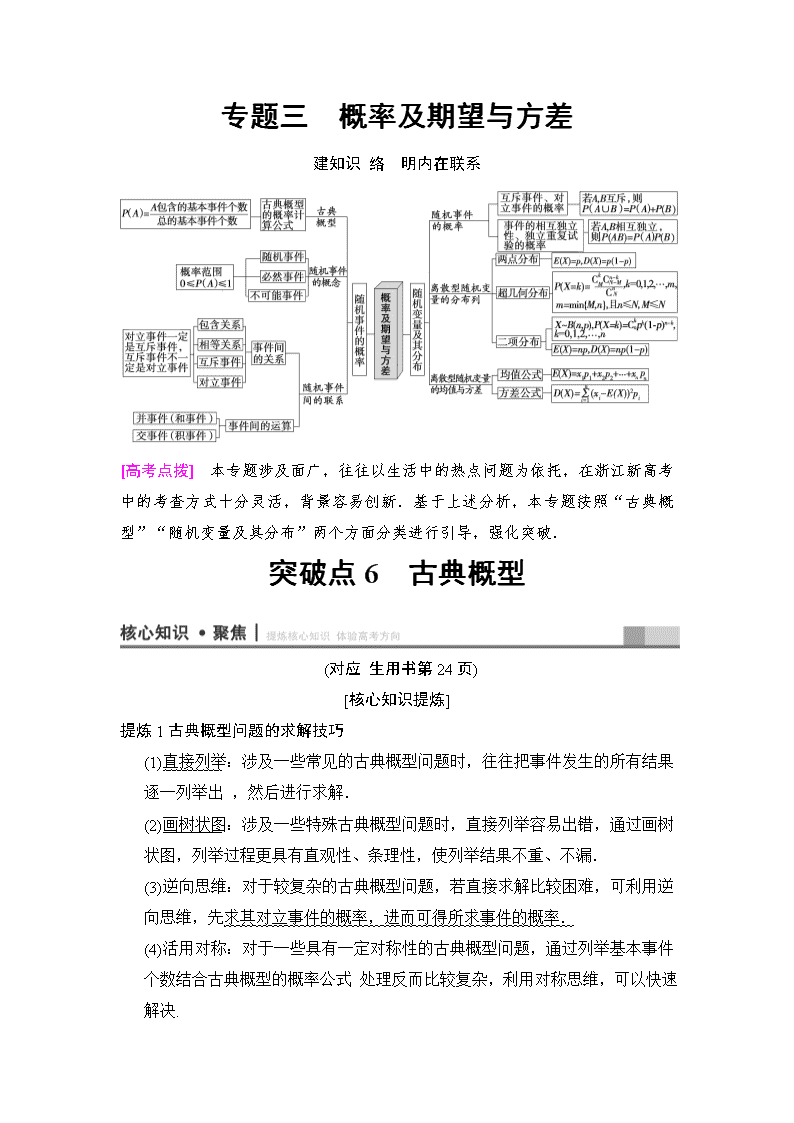
专题三　概率及期望与方差 建知识 络　明内在联系 ‎[高考点拨]　本专题涉及面广，往往以生活中的热点问题为依托，在浙江新高考中的考查方式十分灵活，背景容易创新．基于上述分析，本专题按照“古典概型”“随机变量及其分布”两个方面分类进行引导，强化突破．‎ 突破点6　古典概型 ‎ (对应 生用书第24页)‎ ‎[核心知识提炼]‎ 提炼1古典概型问题的求解技巧 ‎ (1)直接列举：涉及一些常见的古典概型问题时，往往把事件发生的所有结果逐一列举出 ，然后进行求解．‎ ‎ (2)画树状图：涉及一些特殊古典概型问题时，直接列举容易出错，通过画树状图，列举过程更具有直观性、条理性，使列举结果不重、不漏．‎ ‎ (3)逆向思维：对于较复杂的古典概型问题，若直接求解比较困难，可利用逆向思维，先求其对立事件的概率，进而可得所求事件的概率．‎ ‎ (4)活用对称：对于一些具有一定对称性的古典概型问题，通过列举基本事件个数结合古典概型的概率公式 处理反而比较复杂，利用对称思维，可以快速解决.‎ 提炼2求概率的两种常用方法 ‎　 (1)将所求事件转化成几个彼此互斥的事件的和事件，利用概率加法公式求解概率．‎ ‎ (2)若一个较复杂的事件的对立面的分类较少，可考虑利用对立事件的概率公式，即“正难则反”．它常用 求“至少”或“至多”型事件的概率．‎ ‎[高考真题回访]‎ 回访　古典概型 ‎1．(2011·浙江高考)从装有3个红球、2个白球的袋中任取3个球，则所取的3个球中至少有1个白球的概率是(　　)‎ ‎ A.　　　　　 B. ‎ C. D. ‎ D　[“所取的3个球中至少有1个白球”的对立事件是“所取的3个球都不是白球”，因而所求的概率P＝1－＝1－＝.]‎ ‎2．(2014·浙江高考)在3张奖券中有一、二等奖各1张，另1张无奖．甲、乙两人各抽取1张，两人都中奖的概率是________．‎ ‎ 　[记“两人都中奖”为事件A，‎ ‎ 设中一、二等奖及不中奖分别记为1,2,0，那么甲、乙抽奖结果有(1,2)，(1,0)，(2,1)，(2,0)，(0,1)，(0,2)，共6种．‎ ‎ 其中甲、乙都中奖有(1,2)，(2,1)，2种，所以P(A)＝＝.]‎ ‎3．(2013·浙江高考)从3男3女共6名同 中任选2名(每名同 被选中的机会均等)，这2名都是女同 的概率等于__________．‎ ‎ 　[用A，B，C表示三名男同 ，用a，b，c表示三名女同 ，则从6名同 中选出2人的所有选法为：AB，AC，Aa，Ab，Ac，BC，Ba，Bb，Bc，Ca，Cb，Cc，ab，ac，bc，共15种选法，其中都是女同 的选法有3种，即ab，ac，bc，故所求概率为＝.]‎ ‎ (对应 生用书第25页)‎ 热点题型1　古典概型 题型分析：古典概型是高考考查概率的核心，问题背景大多是取球、选人、组数等，求解的关键是准确列举基本事件，难度较小.‎ ‎【例1】　(1)(2017·浙东北教 联盟高三一模考试7)袋子里有大小、形状相同的红球m个，黑球n个(m＞n＞2)．从中任取1个球是红球的概率记为p1.若将红球、黑球个数各增加1个，此时从中任取1个球是红球的概率记为p2；若将红球、黑球个数各减少1个，此时从中任取1个球是红球的概率记为p3，则(　　)‎ ‎ A．p1＞p2＞p3　　　　　 B．p1＞p3＞p2‎ ‎ C．p3＞p2＞p1 D．p3＞p1＞p2‎ ‎ (2)已知M＝{1,2,3,4}，若a∈M，b∈M，则函数f(x)＝ax3＋bx2＋x－3在R上为增函数的概率是(　　)‎ ‎ 【导 号：68334080】‎ ‎ A. B. ‎ C. D. ‎ (1)B　(2)A　[(1)由题意得p1＝，p2＝，p3＝，则＝＝1＋，＝＝1＋，＝＝1＋，则－＝－＝＜0，－＝－＝＞0，所以＞＞，所以p3＞p1＞p2，故选D.‎ ‎ (2)记事件A为“函数f(x)＝ax3＋bx2＋x－3在R上为增函数”．‎ ‎ 因为f(x)＝ax3＋bx2＋x－3，所以f′(x)＝3ax2＋2bx＋1.‎ ‎ 因为函数f(x)在R上为增函数，所以f′(x)≥0在R上恒成立．‎ ‎ 又a>0，所以Δ＝(2b)2－4×‎3a＝4b2－‎12a≤0在R上恒成立，即a≥.‎ ‎ 所以当b＝1时，有a≥，故a可取1,2,3,4，共4个数；‎ ‎ 当b＝2时，有a≥，故a可取2,3,4，共3个数；‎ ‎ 当b＝3时，有a≥3，故a可取3,4，共2个数；‎ ‎ 当b＝4时，有a≥，故a无可取值．‎ ‎ 综上，事件A包含的基本事件有4＋3＋2＝9(种)．‎ ‎ 又a，b∈{1,2,3,4}，所以(a，b)共有4×4＝16(种)．‎ ‎ 故所求事件A的概率为P(A)＝.故选A.]‎ ‎[方法指津]‎ 利用古典概型求事件概率的关键及注意点 ‎1．关键：正确列举出基本事件的总数和待求事件包括的基本事件数．‎ ‎2．注意点：(1)对于较复杂的题目，列出事件数时要正确分类，分类时应不重不漏．‎ ‎(2)当直接求解有困难时，可考虑求其对立事件的概率．‎ ‎[变式训练1]　(2016·温州调研)若将甲、乙两个球随机放入编号为1,2,3的三个盒子中，每个盒子的放球数量不限，则在1,2号盒子中各有一个球的概率是________．‎ ‎ 　[将甲、乙两个球随机放入编号为1,2,3的三个盒子中，每个盒子的放球数量不限，则有3×3＝9种不同放法，其中在1,2号盒子中各有一个球的结果有2种，故所求概率是.]‎ 热点题型2　互斥事件与对立事件的概率 题型分析：互斥事件与对立事件的概率常与古典概型等交汇命题，主要考查 生的分析转化能力，难度中等.‎ ‎【例2】　现有甲、乙、丙、丁4个 生课余参加 校社团文 社与街舞社的活动，每人参加且只能参加一个社团的活动，且参加每个社团是等可能的．‎ ‎ (1)求文 社和街舞社都至少有1人参加的概率；‎ ‎ (2)求甲、乙同在一个社团，且丙、丁不同在一个社团的概率．‎ ‎ [解]　甲、乙、丙、丁4个 生课余参加 校社团文 社与街舞社的情况如下：‎ 文 社 街舞社 ‎1‎ 甲乙丙丁 ‎2‎ 甲乙丙 丁 ‎3‎ 甲乙丁 丙 ‎4‎ 甲丙丁 乙 ‎5‎ 乙丙丁 甲 ‎6‎ 甲乙 丙丁 ‎7‎ 甲丙 乙丁 ‎8‎ 乙丙 甲丁 ‎9‎ 甲丁 乙丙 ‎10‎ 乙丁 甲丙 ‎11‎ 丙丁 甲乙 ‎12‎ 甲 乙丙丁 ‎13‎ 乙 甲丙丁 ‎14‎ 丙 甲乙丁 ‎15‎ 丁 甲乙丙 ‎16‎ 甲乙丙丁 ‎ 共有16种情形，即有16个基本事件. 6分 ‎ (1)文 社或街舞社没有人参加的基本事件有2个，‎ ‎ 故所求概率为＝. 9分 ‎ (2)甲、乙同在一个社团，且丙、丁不同在一个社团的基本事件有4个，故所求概率为＝. 12分 ‎[方法指津]‎ ‎1．直接求法：将所求事件分解为一些彼此互斥事件的和，运用互斥事件概率的加法公式计算．‎ ‎2．间接求法：先求此事件的对立事件，再用公式P(A)＝1－P()求解，即运用逆向思维(正难则反)，特别是“至多”“至少”‎ 型题目，用间接求法会较简便．‎ 提醒：应用互斥事件概率的加法公式的前提是确定各个事件是否彼此互斥．‎ ‎[变式训练2]　(名师押题)根据以往统计资料，某地车主购买甲种保险的概率为0.5，购买乙种保险但不购买甲种保险的概率为0.3.‎ ‎ (1)求该地1位车主至少购买甲、乙两种保险中的1种的概率；‎ ‎ (2)求该地1位车主甲、乙两种保险都不购买的概率．‎ ‎ 【导 号：68334081】‎ ‎ [解]　记事件A为“该车主购买甲种保险”，事件B为“该车主购买乙种保险但不购买甲种保险”，事件C为“该车主至少购买甲、乙两种保险中的1种”，事件D为“该车主甲、乙两种保险都不购买”. 4分 ‎ (1)由题意得P(A)＝0.5，P(B)＝0.3， 6分 ‎ 又C＝A∪B，所以P(C)＝P(A∪B)＝P(A)＋P(B)＝0.5＋0.3＝‎0.8. 12‎分 ‎ (2)因为D与C是对立事件，所以P(D)＝1－P(C)＝1－0.8＝‎0.2. 15‎分