2019届二轮复习割补法第2课课件（25张）（全国通用）

2019届二轮复习割补法第2课课件（25张）（全国通用）

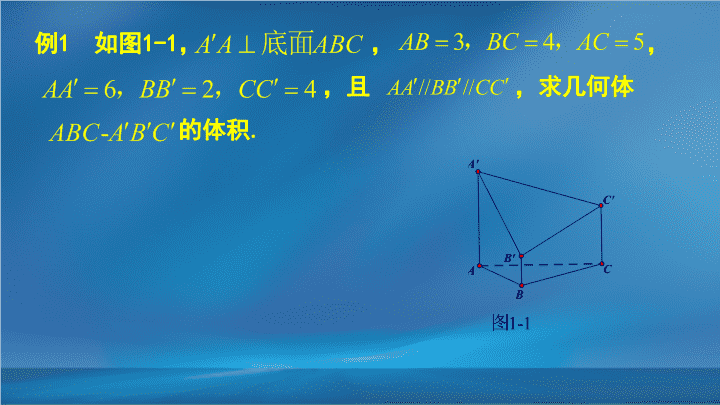
中学数学解题思想方法--割补法 第二讲：割补法的灵活运用 与专题总结 立体几何中运用割补思想 在求不规则的几何体的体积时，有些题目采用“补形法”比较容易；有些题目采用“分割法”更为恰当；还有些题目既能采用“补形法”解决，也能采用“分割法”解决；还有些题目既要采用“补形法”，同时采用“分割法”才易解决. 例 1 如图 1 - 1 ， ， ， ，且 ， 求 几何体 的体积 . 分析 本题所给几何体不是一个规则的几何体，可以看成一个直三棱柱被一个平面所截而成的.根据题目特点我们既可以选择“补形法”补成直三棱柱，如 图 1 - 2 所 示，计算出直三棱柱的体积，再利用直三棱柱和已知几何体的关系 求解 . 也 可以采用“分割法”，把所给几何体分割成直三棱柱和四棱锥，如 图 1 - 3 所 示来解决 . 解 法一： 补上一个相同的几何体如 图 1-2 所 示 ， 因为 ， ， 则新几何体的体积等于两个原几何体的体积 . 即 所以新几何体 为 直三棱柱 ， 所以原几何体的体积 为 24 . 解 法二： 在 上取一点 使 ，在 上取 一点 使 , 连 结 ， 如图 1-3 所 示， 为 直三棱柱 过点 作 ， 如图 1-4 所示 . 所以所求几何体的体积为 评析： 本题解法一采取的解题方法为补形法 ，解法二所采取的解题方法为分割法.两种方法都比较自然，由于题目所给条件，本题采用解法一较为简捷. 例 2 如 图 2 -1 ， , 四边形 为正方形 , ，求 几何体 的 体积 . 分析 本题 所给几何体可以看成用一个平面截长方体而成 . 由于 因此可以考虑补成如图 5-14 所示的一个正方体 . 新 几何体由一个正方体和一个三 棱锥组成 . 新几何体与原几何体相比，多了一 个三棱锥 容易得三 棱锥 与三 棱锥 体积 相等， 这样 本题 所给几何体 的体积就是一个正方体的体积 . 解： 在 上 截取 , 延长 至 使 . 四边形 为 正方形 , 且 所以 所求几何体的 体积 为 评析： 本题灵活运用“割补思想”采用“补形法”与“分割法”相结合的解题策略化难为易.近几年高考中求几何体体积经常以三视图的形式呈现， 这样 既 考察三视图同时又考察空间几何体的体积计算 .本题可以用三视图的形式呈现，这样更符合近几年高考趋势. 具体如下：一个几何体的三视图如图所示，求该几何体的体积. 例 3 某 几何体的三视图如图所示 , 则该几何体的体积为 ________. 分析 由 几何体的三视图还原成直观图如图 3-1 ， 可知 平面 , ， ， ， . 由前面的知识我们不难发现既可以用“补形法”，如图 3-2 所示，也 可以 用“分割法”如图 3-3 所示来求解 . 延长 至 使 , 连结 如 图 3-2 所示 . 解： 由 几何体的三视图还原成直观图如图 3-1 ， 可知 平面 , ， ， ， . 所以 所求几何体的 体积 评析： 本题难点之一是把三视图还原成直观图，实际还原成几何体后我们选择的方法就比较灵活了 . 我们既可以有上面解法中“补形法”，也可以 用如 图 3-3 中 的“分割法” . 近几年 的高考中 这种呈现方式比较 流行 . 专题总结 立体几何中割补思想的运用常见的方法有三种：补形法、分割法、补形与分割相结合.三种方法共同之处都是将复杂的、不规则的、不易认识的几何体，通过“分割”或者“补形”转化为简单的、规则的、易于计算体积的几何体. 补形法中将原图形补成一个新的几何体体现了构造的方法，需要对常见的几何体模型有深刻的认识.分割法中可以从几何体的外部或者内部进行分割，再利用部分与整体的关系来解决问题.近几年的高考中割补法的题目常以三视图的形式呈现，一般要根据三视图先画出直观图，再利用割补法求解. 谢谢！