四川省仁寿第一中学北校区2019-2020学年高二6月月考（期中）数学（理）试题

四川省仁寿第一中学北校区2019-2020学年高二6月月考（期中）数学（理）试题

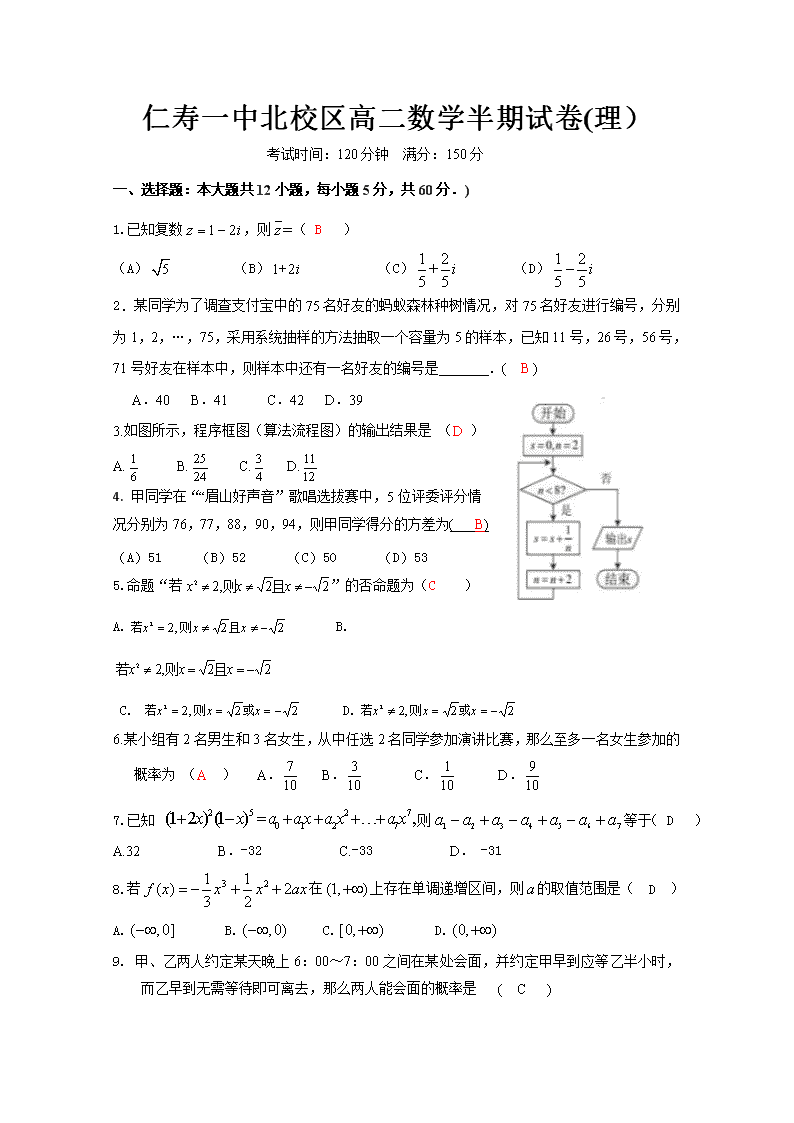
仁寿一中北校区高二数学半期试卷(理）‎ 考试时间：120分钟 满分：150分 一、选择题：本大题共12小题，每小题5分，共60分．)‎ ‎1.已知复数，则（ B ）‎ ‎（A） （B） （C） （D）‎ ‎2．某同学为了调查支付宝中的75名好友的蚂蚁森林种树情况，对75名好友进行编号，分别为1，2，…，75，采用系统抽样的方法抽取一个容量为5的样本，已知11号，26号，56号，71号好友在样本中，则样本中还有一名好友的编号是　 　．( B )‎ A．40 B．41 C．42 D．39‎ ‎3.如图所示，程序框图（算法流程图）的输出结果是 （D ）‎ A. B. C. D.‎ ‎4. 甲同学在““眉山好声音”歌唱选拔赛中，5位评委评分情况分别为76，77，88，90，94，则甲同学得分的方差为( B)‎ ‎（A）51 （B）52 （C）50 （D）53‎ ‎5.命题“若”的否命题为（C ）‎ A. B. ‎ ‎ C. D.‎ ‎6.某小组有2名男生和3名女生，从中任选2名同学参加演讲比赛，那么至多一名女生参加的概率为 （A ） A． B． C． D．‎ ‎7.已知 则等于（ D ） A.32 B．-32 C.-33 D． -31‎ ‎8.若在上存在单调递增区间，则的取值范围是（ D ） A. B. C. D.‎ ‎9. 甲、乙两人约定某天晚上6：00～7：00之间在某处会面，并约定甲早到应等乙半小时，而乙早到无需等待即可离去，那么两人能会面的概率是 ( C )‎ A． B． C． D．‎ ‎10.从0、1、2、3、4、5中选出四个数，组成没有重复数字的四位数，其中偶数有（A )‎ A．156 B． 108 C．360 D．180‎ ‎11.《九章算术》中割圆术有：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣.”其体现的是一种无限与有限的转化过程，比如在中“”即代表无限次重复，但原式却是个定值，这可以通过方程确定，则是（ A ）（A） （B） （C） （D）‎ ‎12.已知函数的导数满足对恒成立，且实数满足，则下列关系式恒成立的是（ D ）‎ ‎（A） （B） （C） （D）‎ 二、填空题：本大题共4小题，每小题5分，共20分．‎ ‎13.（为虚数单位）的虚部是 . ‎ ‎14.已知，则函数的值域是 .‎ ‎15.从5名学生中选出4名分别参加数学，物理，化学，生物竞赛，其中甲不能参加生物竞赛，则不同的参赛方案种数为 96 .‎ ‎16.已知函数若方程恰有两个实根，‎ 则实数的取值范围是 . ‎ 三、 解答题：本大题共6小题，共70分.其中17题10分，18—22题每小题12分 ‎17.已知二项式； ‎ （1） 若展开式中第5项为常数项，求其常数项。‎ （2） 若展开式中第2项、第3项、第4项的二项式系数成等差数列，求展开式中二项式系数最大的项。‎ 解：（1）n=6,常数项为60.‎ （1） n=7,二项式系数最大的项是第四项和第五项 ‎18.已知命题；‎ （1） 若为真命题，求实数的取值范围；‎ （1） 已知命题当为假命题，为真命题时，求实数m的取值范围。‎ ‎19．某校在高二数学竞赛初赛后，对90分及以上的成绩进行统计，其频率分布直方图如图所示，若[130,140]分数段的参赛学生人数为2.‎ ‎(1)求该校成绩在[100,120]分数段的参赛学生人数；‎ ‎(2)估计90分及以上的学生成绩的众数、中位数和平均数(结果保留整数）‎ 解：（1）28人 (2) 众数：115 中位数：113 平均数为113‎ ‎20.某大型商场的空调在1月至5月的销售量与月份相关，得到的统计数据如表：‎ 月份x ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 销量y(百台)‎ ‎0.6‎ ‎0.8‎ ‎1.2‎ ‎1.6‎ ‎1.8‎ （1） 经分析发现1月份到5月份的销售量可用线性回归模型拟合商场空调的月销量Y（百件）与月份X之间的相关关系。请用最小二乘法求Y关于X的线性回归方程＝x＋，并预测6月份该商场空调的销售量；‎ ‎（2）若该商场的营销部对空调进行新一轮促销，对7月12月有购买空调意愿的顾客进行问卷调查。假设该地拟购买空调的消费群体十分宏大，经过营销部调研机构对其中的500名顾客进行了一个抽样调查，得到如下一份频数表：‎ 有购买意愿对应的月份 ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 频数 ‎60‎ ‎80‎ ‎120‎ ‎130‎ ‎80‎ ‎30‎ 现采用分层抽样的方法从购买意愿的月份在7月与12月的这90名顾客中随机抽取6名，再从这6人中随机抽取3人进行跟踪调查，求抽出的3 人中恰好有2人是购买意愿的月份是12月的概率。‎ ‎ (附：对于线性回归方程＝x＋，其中）‎ 答案：（1） 6月份的销售量为2.16百台 （或216台） （2）p=1/5‎ ‎21.已知函数，其中．‎ ‎（Ⅰ）讨论函数的单调性；‎ ‎（Ⅱ）当时，若恒成立，求实数的范围．‎ 22. 已知函数.‎ ‎（1）讨论的极值； （2）若有两个零点，证明：‎ 解（1）当时，无极值 当时,有极小值