2018届二轮复习双曲线课件（全国通用）

2018届二轮复习双曲线课件（全国通用）

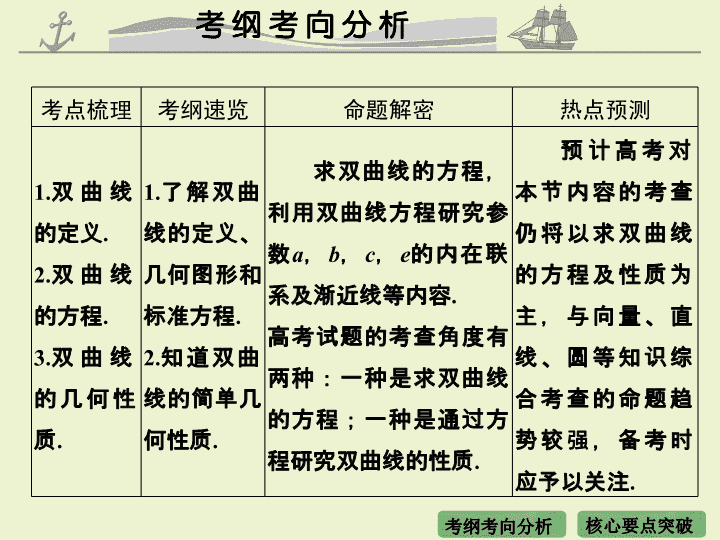
第 四 节　 双曲线 考点梳理 考纲速览 命题解密 热点预测 1. 双曲线的定义 . 2. 双曲线的方程 . 3. 双曲线的几何性质 . 1. 了解双曲线的定义、几何图形和标准方程 . 2. 知道双曲线的简单几何性质 . 　　求双曲线的方程，利用双曲线方程研究参数 a ， b ， c ， e 的内在联系及渐近线等内容 . 高考试题的考查角度有两种：一种是求双曲线的方程；一种是通过方程研究双曲线的性质 . 　　预计高考对本节内容的考查仍将以求双曲线的方程及性质为主，与向量、直线、圆等知识综合考查的命题趋势较强，备考时应予以关注 . 知识点一 双曲线的定义及方程 1. 双曲线的定义 双曲线的两焦点 F 1 、 F 2 之间的距离 | F 1 F 2 | ＝ 2 c ，对双曲线上任意一点 M 都有 || MF 1 | － | MF 2 || ＝ 2 a <2 c . 这个条件是必要的，否则其轨迹就不是双曲线 . 事实上，若 2 a ＝ 2 c ，其轨迹是以 F 1 、 F 2 为端点且方向相反的 ；若 2 a >2 c ，其轨迹 . 两条射线 不存在 2. 双曲线的方程 求双曲线的标准方程也是从 “ 定形 ”“ 定式 ” 和 “ 定量 ” 三个方面去考虑 . “ 定形 ” 是指对称中心在原点，以坐标轴为对称轴的情况下，焦点在哪条坐标轴上； “ 定式 ” 根据 “ 形 ” 设双曲线方程的具体形式； “ 定量 ” 是指用定义法或待定系数法确定 a ， b 的值 . 若双曲线的焦点在 x 轴上，可设双曲线方程为 _________ ( a >0 ， b >0) ；若双曲线的焦点在 y 轴上，可设双曲线方程为 _________ ( a >0 ， b >0) ；若焦点位置无法确定时，可设双曲线方 程为 ( mn >0) 或 Ax 2 － By 2 ＝ 1( AB >0) 的形式，这样可避开讨论，减少运算量 . 知识点二 双曲线的几何性质 1. 双曲线的几何性质 x ≥ a 或 x ≤ － a y ≥ a 或 y ≤ － a 性质 对称性 对称轴： x 轴， y 轴对称 中心 ： _________ 对称轴： x 轴， y 轴 对称中心：坐标原点 顶点坐标 A 1 ( － a ， 0) ， A 2 ( a ， 0) A 1 (0 ，－ a ) ， A 2 (0 ， a ) 焦点坐标 (± c ， 0) (0 ， ± c ) 渐近线 ———— 离心率 e ＝ ， e ∈ ________ 实虚轴 线段 A 1 A 2 叫做双曲线的实轴，它的长 | A 1 A 2 | ＝ 2 a ；线段 B 1 B 2 叫做双曲线的虚轴，它的长 | B 1 B 2 | ＝ 2 b ； a 叫做双曲线的半实轴长， b 叫做双曲线的半虚轴长 a ， b ， c 间的关系 c 2 ＝ a 2 ＋ b 2 ( c > a >0 ， c > b >0) 坐标原点 (1 ， ＋ ∞ ) 2. 等轴双曲线 实轴与虚轴等长的双曲线叫做等轴双曲线，其方程为 x 2 － y 2 ＝ λ ( λ ≠ 0) ，其离心率为 e ＝ ____ ，渐近线方程为 ________ . y ＝ ± x 方法 1 双曲线的几何性质 求双曲线离心率、渐近线问题的一般方法 答案　 B 方法 2 求焦点不定的双曲线方程 双曲线标准方程的求解步骤：