人教版高三数学总复习课时作业63
课时作业63 算法初步
一、选择题
1.当a=1,b=3时,执行完如图的一段程序后x的值是( )
A.1 B.3 C.4 D.-2
解析:∵a
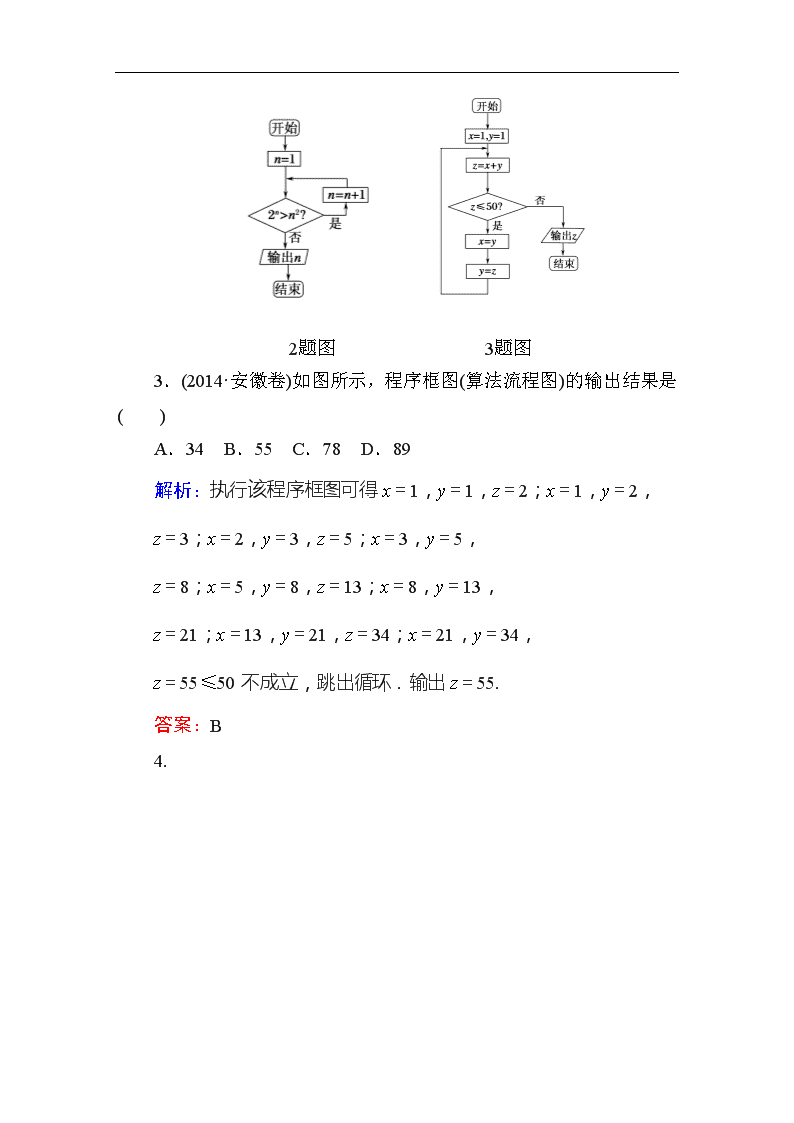
12成立,当n=2时,22>22不成立,所以输出n=2,故选B.
答案:B
3.(2014·安徽卷)如图所示,程序框图(算法流程图)的输出结果是( )
A.34 B.55 C.78 D.89
解析:执行该程序框图可得x=1,y=1,z=2;x=1,y=2,
z=3;x=2,y=3,z=5;x=3,y=5,
z=8;x=5,y=8,z=13;x=8,y=13,
z=21;x=13,y=21,z=34;x=21,y=34,
z=55≤50不成立,跳出循环.输出z=55.
答案:B
4.
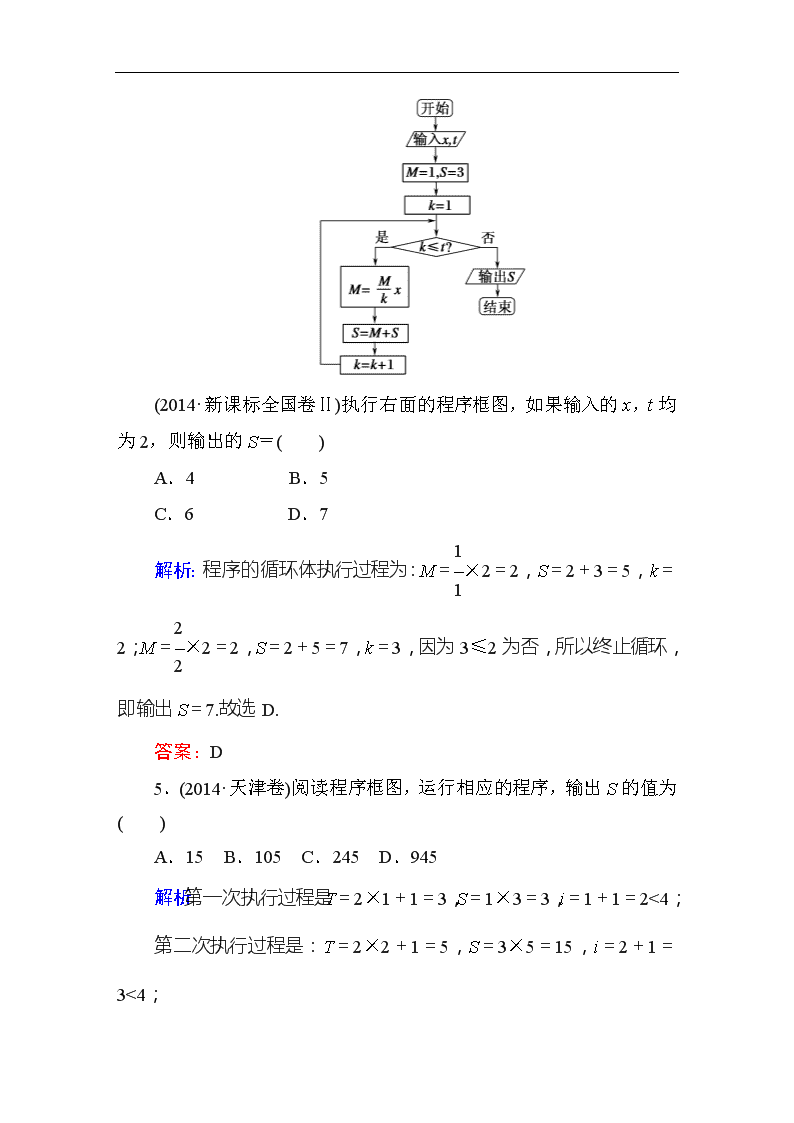
(2014·新课标全国卷Ⅱ)执行右面的程序框图,如果输入的x,t均为2,则输出的S=( )
A.4 B.5
C.6 D.7
解析:程序的循环体执行过程为:M=×2=2,S=2+3=5,k=2;M=×2=2,S=2+5=7,k=3,因为3≤2为否,所以终止循环,即输出S=7.故选D.
答案:D
5.(2014·天津卷)阅读程序框图,运行相应的程序,输出S的值为( )
A.15 B.105 C.245 D.945
解析:第一次执行过程是:T=2×1+1=3,S=1×3=3,i=1+1=2<4;
第二次执行过程是:T=2×2+1=5,S=3×5=15,i=2+1=3<4;
第三次执行过程是:T=2×3+1=7,S=15×7=105,i=3+1=4≥4,
此时输出S=105,故选B.
答案:B
6.如图所示,x1,x2,x3为某次考试三个评阅人对同一道题的独立评分,p为该题的最终得分,当x1=6,x2=9,p=9.5时,x3等于( )
A.10 B.9 C.8 D.7
解析:x1=6,x2=9,|x1-x2|=3,|x3-6|<|x3-9|不成立,取x1=x3⇒x3+9=9.5×2⇒x3=10,故选A.
答案:A
二、填空题
7.
(2014·辽宁卷)执行右面的程序框图,若输入n=3,则输出T
=________.
解析:初始值:i=0,S=0,T=0;
i=1,S=1,T=1;
i=2,S=3,T=4;
i=3,S=6,T=10;
i=4>3,S=10,输出T=10+10=20.
答案:20
8.(2014·湖北卷)阅读如图所示的程序框图,运行相应的程序,若输入n的值为9,则输出S的值为________.
解析:由程序框图知,S=21+22+…+29+1+2+…+9=1 067.
答案:1 067
9.(2014·湖北卷)设a是一个各位数字都不是0且没有重复数字的三位数,将组成a的3个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a)(例如a=815,则I(a)=158,D(a)=851).阅读如上图所示的程序框图,运行相应的程序,任意输入一个a,输出的结果b=________.
解析:当a=123时,b=321-123=198≠123;
当a=198时,b=981-189=792≠198;
当a=792时,b=972-279=693≠792;
当a=693时,b=963-369=594≠693;
当a=594时,b=954-459=495≠594;
当a=495时,b=954-459=495=a.
故填495.
答案:495
三、解答题
10.已知函数f(x)=
(1)若f(x)=16,求相应x的值;
(2)画程序框图,对于输入的x值,输出相应的f(x)值.
解:(1)当x<0时,f(x)=16,即(x+2)2=16,解得x=-6;
当x>0时,f(x)=16,即(x-2)2=16,解得x=6.
(2)程序框图如图所示:
11.已知某算法的程序框图如图所示,若将输出的(x,y)值依次记为(x1,y1)、(x2,y2)、…、(xn,yn)、…若程序运行中输出的一个数组是(x,-8),求x的值.
解:开始n=1,x1=1,y1=0→n=3,x2=3,y2=-2→n=5,x3=9,y3=-4→n=7,x4=27,y4=-6→n=9,x5=81,y5=-8,则x=81.
1.(2014·北京卷)当m=7,n=3时,执行如图所示的程序框图,输出的S值为( )
A.7 B.42 C.210 D.840
解析:开始:m=7,n=3.
计算:k=7,S=1.
第一次循环,此时m-n+1=7-3+1=5,显然k<5不成立,所以S=1×7=7,k=7-1=6.
第二次循环,6<5不成立,所以S=7×6=42,k=6-1=5.
第三次循环,5<5不成立,所以S=42×5=210,k=5-1=4.
显然4<5成立,输出S的值,即输出210,故选C.
答案:C
2.阅读如图所示的程序框图,则输出结果s的值为( )
A. B.
C. D.
解析:程序在执行过程中,s,n的值依次为:s=1,n=1;s=1×cos,n=2;s=1×cos×cos,n=3;s=1×cos×cos×cos,n=4;s=1×cos×cos×cos×cos,n=5,输出s=1×cos×cos×cos×cos==.
答案:D
3.执行如图所示的程序框图,输出的结果是________.
解析:共循环2 013次,由裂项求和得S=++…+=(1-)+(-)+…+(-)=1-=.
答案:
4.某算法的程序框图如图所示,其中输入的变量x在1,2,3,…,24这24个整数中等可能随机产生.
(1)分别求出按程序框图正确编程运行时输出y的值为i的概率Pi(i=1,2,3);
(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序
重复运行n次后,统计记录了输出y的值为i(i=1,2,3)的频数.以下是甲、乙所作频数统计表的部分数据.
甲的频数统计表(部分)
运行次
数n
输出y的值
为1的频数
输出y的值
为2的频数
输出y的值
为3的频数
30
14
6
10
…
…
…
…
2 100
1 027
376
697
乙的频数统计表(部分)
运行次
数n
输出y的值
为1的频数
输出y的值
为2的频数
输出y的值
为3的频数
30
12
11
7
…
…
…
…
2 100
1 051
696
353
当n=2 100时,根据表中的数据,分别写出甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率(用分数表示),并判断两位同学中哪一位所编程序符合算法要求的可能性较大.
解:(1)变量x是在1,2,3,…,24,这24个整数中随机产生的一个数,共有24种可能.
当x从1,3,5,7,9,11,13,15,17,19,21,23这12个数中产生时,输出y的值为1,故P1=;
当x从2,4,8,10,14,16,20,22这8个数中产生时,输出y的值为2,故P2=;
当x从6,12,18,24这4个数中产生时,输出y的值为3,故P3=
.
所以,输出y的值为1的概率为,输出y的值为2的概率为,输出y的值为3的概率为.
(2)当n=2 100时,甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率如下:
输出y的值
为1的频率
输出y的值
为2的频率
输出y的值
为3的频率
甲
乙
比较频率趋势与概率,可得乙同学所编程序符合算法要求的可能性较大.