2018届二轮复习专题2第1讲函数的图象与性质课件（57张）（全国通用）

2018届二轮复习专题2第1讲函数的图象与性质课件（57张）（全国通用）

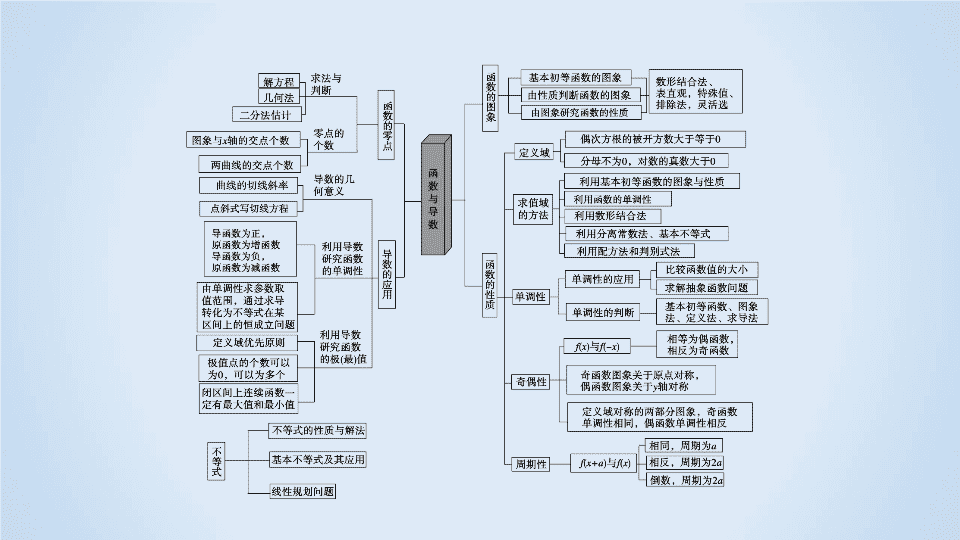
第一部分 专题强化突破 专题二　函数、不等式、导数 知识网络构建 第一讲 　 函数的图象与性质 1 高考考点聚焦 2 核心知识整合 3 高考真题体验 4 命题热点突破 5 课后强化训练 高考考点聚焦 高考考点 考点解读 函数的概念及其表示 1. 求具体函数的定义域、值域 2 ．以分段函数为载体考查求函数值或已知函数值求字母的值 ( 或取值范围 ) 等 函数的图象及其应用 1. 以具体函数的解析式选择图象或知图象选解析式 2 ．利用函数的图象研究函数的性质 ( 特别是单调性、最值、零点 ) 、方程解的问题及解不等式、比较大小等 函数的性质及其应用 1. 确认函数的单调性、奇偶性、周期性、对称性及最值 2 ．综合应用函数的性质求值 ( 取值范围 ) 、比较大小等，常与不等式相结合 备考策略 本部分内容在备考时应注意以下几个方面： (1) 深刻理解函数、分段函数及函数的单调性、奇偶性、最值、周期性等概念． (2) 掌握各种基本初等函数的定义、图象和性质，以及幂和对数的运算性质． (3) 掌握函数图象的作法、变换法则及利用图象解决函数性质、方程、不等式问题的方法． (4) 掌握利用函数性质比较大小、求值、求参数范围等问题的方法． 预测 2018 年命题热点为： (1) 求函数定义域及与分段函数有关的求值、求范围等问题． (2) 给出函数解析式选图象及利用图象解决交点个数、方程的解、不等式等问题． (3) 利用函数的性质求值，求参数取值范围、比较大小等问题． 核心知识整合 1 ． 指数与对数式的七个运算公式 (1) a m · a n ＝ __________ ． (2)( a m ) n ＝ __________ ． (3)log a ( MN ) ＝ ______________ ( a >0 且 a ≠ 1 ， M >0 ， N >0) ． a m ＋ n 　 a mn 　 log a M ＋ log a N 　 log a M － log a N 　 n log a M 　 N 　 2 ． 单调性定义 如果对于 ____________________ 上的 __________ 两个自变量的值 x 1 ， x 2 ，且 ________ ，都有 ____________ 成立，则 f ( x ) 在 D 上是 ________( 都有 ___________ 成立，则 f ( x ) 在 D 上是 __________ ) ． 3 ． 奇偶性定义 对于定义域内的任意 x (______________________ ) ，都有 _________________ 成立，则 f ( x ) 为奇函数 ( 都有 _______________ 成立，则 f ( x ) 为偶函数 ) ． 4 ． 周期性定义 周期函数 f ( x ) 的最小正周期 T 必须满足下列两个条件： (1) 当 x 取定义域内的每一个值时，都有 _______________ ． (2) T 是 _____________________ ． 定义域 I 内某个区间 D 　 任意　 x 1 < x 2 　 f ( x 1 )< f ( x 2 ) 　 增函数　 f ( x 1 )> f ( x 2 ) 　 减函数　 定义域关于原点对称　 f ( － x ) ＝－ f ( x 2 ) 　 f ( － x ) ＝ f ( x ) 　 f ( x ＋ T ) ＝ f ( x ) 　 不为零的最小正数　 5 ． 指数函数与对数函数的图象和性质 0< a <1 　 递减　 a >1 　 递增　 0< a <1 　 递减　 a >1 　 递增　 指数函数 对数函数 函数值性质 0< a <1 ， 当 x >0 时， 0< y <1 ； 当 x <0 时， y >1 0< a <1 ， 当 x >1 时， y <0 ； 当 0< x <1 时， y >0 a >1 ， 当 x >0 时， y >1 ； 当 x <0 时， 0< y <1 a >1 ， 当 x >1 时， y >0 ； 当 0< x <1 时， y <0 3 ． 函数图象的变换规则 (1) 平移变换 将 y ＝ f ( x ) 的图象向左 ( a >0) 或向右 ( a <0) 平移 | a | 个单位得到 y ＝ f ( x ＋ a ) 的图象； 将 y ＝ f ( x ) 的图象向上 ( a >0) 或向下 ( a <0) 平移 | a | 个单位得到 y ＝ f ( x ) ＋ a 的图象． (2) 对称变换 ① 作 y ＝ f ( x ) 关于 y 轴的对称图象得到 y ＝ f ( － x ) 的图象； ② 作 y ＝ f ( x ) 关于 x 轴的对称图象得到 y ＝－ f ( x ) 的图象； ③ 作 y ＝ f ( x ) 关于原点的对称图象得到 y ＝－ f ( － x ) 的图象； ④ 将 y ＝ f ( x ) 在 x 轴下方的图象翻折到上方，与 y ＝ f ( x ) 在 x 轴上方的图象结合起来得到 y ＝ | f ( x )| 的图象； ⑤ 将 y ＝ f ( x ) 在 y 轴左侧部分去掉，再作右侧关于 y 轴的对称图象合起来得到 y ＝ f (| x |) 的图象． 1 ． 忽略函数的定义域 在判断函数的单调性时，要注意函数的定义域优先；在判断函数的奇偶性时，忽略函数的定义域会导致结论错误． 2 ． 错用集合运算符号 函数的多个单调区间若不连续，不能用符号 “ ∪” 连接，可用 “ 和 ” 或 “ ， ” 连接． 3 ． 忽略基本初等函数的形式、定义和性质 如讨论指数函数 y ＝ a x ( a >0 且 a ≠ 1) 的单调性时，不讨论底数的取值；忽略 a x >0 的隐含条件；幂函数的性质记忆不准确． 高考真题体验 A 　 C 　 C 　 [ 解析 ] 　 依题意 a ＝ g ( － log 2 5.1) ＝ ( － log 2 5.1)· f ( － log 2 5.1) ＝ log 2 5.1 f (log 2 5.1) ＝ g (log 2 5.1) ． 因为 f ( x ) 在 R 上是增函数，可设 0< x 1 < x 2 ， 则 f ( x 1 )< f ( x 2 ) ． 从而 x 1 f ( x 1 )< x 2 f ( x 2 ) ，即 g ( x 1 )< g ( x 2 ) ． 所以 g ( x ) 在 (0 ，＋ ∞ ) 上也为增函数． 又 log 2 5.1>0,2 0.8 >0,3>0 ， 且 log 2 5.1log 2 5.1>2 0.8 >0 ， 所以 c > a > b ． 故选 C ． D 　 [ 解析 ] 　 ∵ f ( x ) 为 R 上的奇函数， f (1) ＝－ 1 ， ∴ f ( － 1) ＝－ f (1) ＝ 1 ， 由－ 1 ≤ f ( x － 2) ≤ 1 ，得 f (1) ≤ f ( x － 2) ≤ f ( － 1) ， 又 ∵ f ( x ) 在 ( － ∞ ，＋ ∞ ) 上单调递减， ∴ － 1 ≤ x － 2 ≤ 1 ， ∴ 1 ≤ x ≤ 3 ，故选 D ． D 　 [ 解析 ] 　 由 x 2 － 2 x － 8>0 ，得 x < － 2 或 x >4 ． 令 g ( x ) ＝ x 2 － 2 x － 8 ，函数 g ( x ) 在 (4 ，＋ ∞ ) 上单调递增，在 ( － ∞ ，－ 2) 上单调递减， ∴ 函数 f ( x ) 的单调递增区间为 (4 ，＋ ∞ ) ． 故选 D ． D 　 A 　 命题热点突破 命题方向 1 　函数的概念与表示 B 　 A 　 『 规律总结 』 1 ． 求函数定义域的方法 (1) 若已知函数的解析式，则函数的定义域是使解析式有意义的自变量的取值范围，只需构建并解不等式 ( 组 ) 即可． (2) 在实际问题或几何问题中除要考虑解析式有意义外，还要使实际问题有意义． 2 ． 求函数值的三个关注点 (1) 形如 f ( g ( x )) 的函数求值，要遵循先内后外的原则． (2) 对于分段函数求值，应注意依据条件准确地找出利用哪一段求解． (3) 对于周期函数要充分利用好周期性． 3 ． 函数值域的求法 求解函数值域的方法有：公式法、图象法、分离常数法、判别式法、换元法、数形结合法、有界性法等，要根据问题具体分析，确定求解的方法 ． C 　 [ － 3,1] 　 [ 解析 ] 　 由 3 － 2 x － x 2 ≥ 0 得 x 2 ＋ 2 x － 3 ≤ 0 ， 即 ( x － 1)( x ＋ 3) ≤ 0 ，解得－ 3 ≤ x ≤ 1 ． 命题方向 2 　函数的图象及其应用 A 　 『 规律总结 』 1 ． 作函数图象的方法及注意点 常用描点法和图象变换法．图象变换法常用的有平移变换、伸缩变换和对称变换．尤其注意 y ＝ f ( x ) 与 y ＝ f ( － x ) ， y ＝－ f ( x ) ， y ＝－ f ( － x ) ， y ＝ f (| x |) ， y ＝ | f ( x )| 及 y ＝ af ( x ) ＋ b 的相互关系． 2 ． 由函数解析式识别函数图象的策略 3 ．函数图象的应用 函数性质的确定与应用及某些方程、不等式等问题的求解，常与函数的图象结合． A 　 D 　 [ 解析 ] 　 由于函数 y ＝ x sin x 是偶函数，由图象知，函数 ① 对应第一个图象；函数 y ＝ x cos x 为奇函数，且当 x ＝ π 时， y ＝－ π<0 ，故函数 ② 对应第三个图象；函数 y ＝ x |cos x | 为奇函数，故函数 ③ 与第四个图象对应；函数 y ＝ x ·2 x 为非奇非偶函数，与第二个图象对应．综上可知，选 D ． 命题方向 3 　函数的性质及其应用 A 　 [ 解析 ] 　 f ( x ) 是偶函数，且在 [0 ，＋ ∞ ) 上是增函数，所以 f ( x )> f (2 x － 1) ⇔ f (| x |)> f (|2 x － 1|) ⇔ | x |>|2 x － 1| ⇔ < x <1. 故选 A ． 『 规律总结 』 函数性质的综合应用类型 1 ． 函数单调性与奇偶性的综合．注意奇、偶函数图象的对称性，以及奇、偶函数在关于原点对称的区间上单调性的关系． 2 ．周期性与奇偶性的综合．此类问题多为求值问题，常利用奇偶性及周期性进行变换，将所求函数值的自变量转化到已知解析式的函数定义域内求解． 3 ．单调性、奇偶性与周期性的综合．解决此类问题通常先利用周期性转化自变量所在的区间，然后利用奇偶性和单调性求解． D 　 [ 解析 ] 　 因为 f (π ) ＝ π 2 ＋ 1 ， f ( － π) ＝－ 1 ，所以 f ( － π) ≠ f (π ) ，所以函数 f ( x ) 不是偶函数，排除 A ；因为函数 f ( x ) 在 ( － 2π ，－ π) 上单调递减，排除 B ；函数 f ( x ) 在 (0 ，＋ ∞ ) 上单调递增，所以函数 f ( x ) 不是周期函数，排除 C ；因为 x >0 时， f ( x )>1 ， x ≤ 0 时，－ 1 ≤ f ( x ) ≤ 1 ，所以函数 f ( x ) 的值域为 [ － 1 ，＋ ∞ ) ． － 10 　 课后强化训练