2018-2019学年吉林省长春汽车经济开发区第三中学高一上学期期中考试数学试题

2018-2019学年吉林省长春汽车经济开发区第三中学高一上学期期中考试数学试题

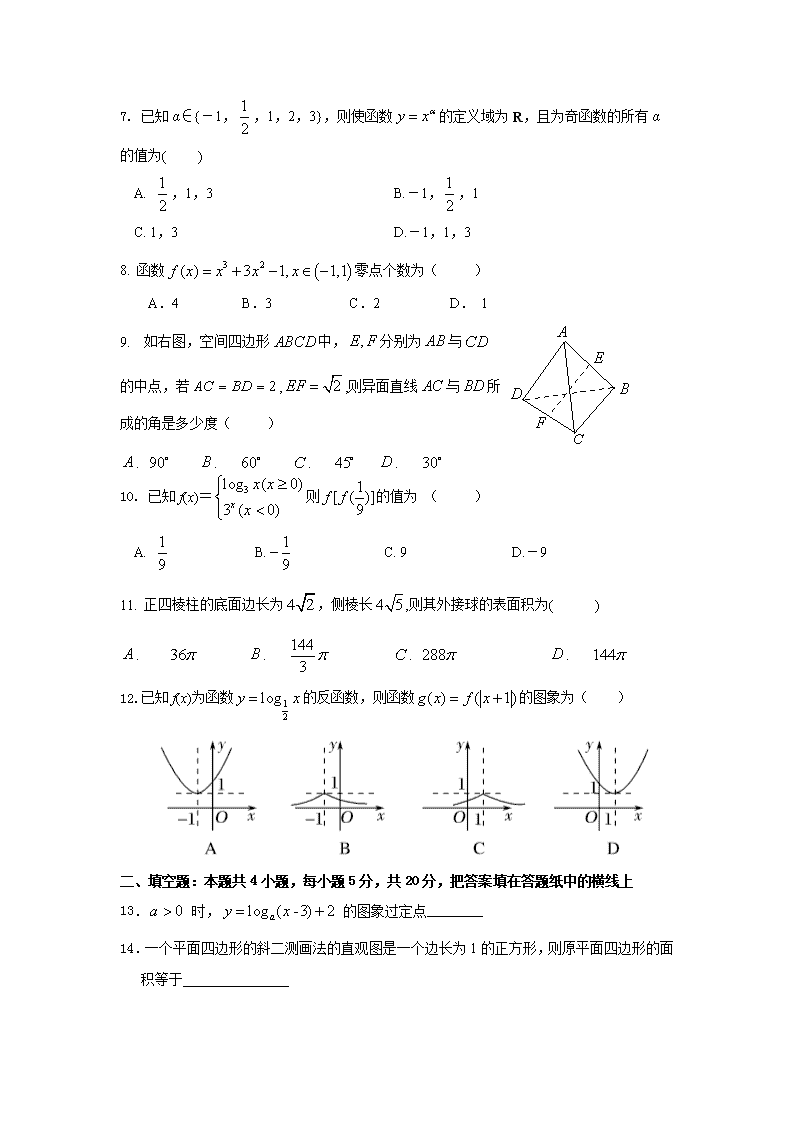
‎2018-2019学年吉林省长春汽车经济开发区第三中学高一上学期期中考试数学试题 注意事项：‎ ‎1、本试卷分试题卷和答题卡，满分120分，考试时间100分钟。 ‎ ‎2、答题前，在答题卡上填写个人相关信息，并将条形码帖到指定位置。‎ ‎3、所有答案必须定在答题卡上，写在试卷上无效。‎ ‎4、考试结束后，只需上交答题卡。‎ ‎.‎ 一、选择题：本题共12小题，每小题5分，共60分，在每小题给出的四个选项中只有一个选项是符合题目要求的．‎ ‎1．已知全集，A是U的子集，且，则集合A是 （ ） ‎ ‎ A．{0，1} B．{0} C．{1} D．‎ ‎2．下列说法不正确的是(　 　)‎ A．圆柱的侧面展开图是一个矩形 B．圆锥的过轴的截面是一个等腰三角形 C．直角三角形绕它的一条边旋转一周形成的曲面围成的几何体是圆锥 D．圆台平行于底面的截面是圆面 ‎3. 设, 用二分法求方程内近似解的过程中, 计算得到则方程的根落在区间（ ）‎ A. （1.5,1.625） B. （1.75,2） C. （1.6875, 1.75） D. （1.625,1.6875）‎ ‎4．已知集合A=，B=，则AB=（ ）‎ A、 B、 C、 D、‎ ‎5. 给出下列命题：‎ ‎ ①直线与平面不平行，则与平面内的所有直线都不平行 ‎ ②直线与平面不垂直，则与平面内的所有直线都不垂直 ‎ ③若两个平面平行，则一个平面内的任一条直线必平行于另一个平面 ‎ ④一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行 其中正确的个数是（ ）‎ ‎ . . . . ‎ ‎6. 一几何体的直观图如图，下列给出的四个俯视图中正确的是(　 　)‎ ‎7. 已知α∈{－1，，1，2，3}，则使函数的定义域为R，且为奇函数的所有α的值为(　 　)‎ A. ，1，3 B.－1，，1 ‎ C. 1，3 D.－1，1，3‎ ‎8. 函数零点个数为（ ） ‎ A．4 B．3 C．2 D． 1‎ ‎9. 如右图，空间四边形中，分别为与 的中点，若,,则异面直线与所 ‎ 成的角是多少度（ ）‎ ‎. . . . ‎ ‎10. 已知f(x)＝则的值为 （ ）‎ A. B. C. 9 D.－9‎ ‎11. 正四棱柱的底面边长为，侧棱长,则其外接球的表面积为( )‎ ‎. . . . ‎ ‎12.已知f(x)为函数的反函数，则函数的图象为（ ）‎ 二、填空题：本题共4小题，每小题5分，共20分，把答案填在答题纸中的横线上 ‎13． 时， 的图象过定点________‎ ‎14．一个平面四边形的斜二测画法的直观图是一个边长为1的正方形，则原平面四边形的面积等于 ‎ ‎15．函数的定义域是 ‎ ‎16．f(x)是定义在R上的单调增函数，满足f(xy)＝f(x)＋f(y)，f(3)＝1，当f(x)≤2时，x的取值范围是 ‎ 三、解答题（本大题4小题，共40分，解答应写出文字说明，证明过程或演算步骤）‎ ‎17. （本小题10分） ‎ 如图，在三角形中，若，，，以所在直线为 轴，将此三角形旋转一周，求所得旋转体的表面积和体积．‎ ‎18. （本小题10分）‎ 记U=R，若集合，，则 ‎（1）求 ； ‎ ‎（2）若集合=，，求的取值范围；‎ ‎19.（本小题10分）‎ 如图，在四棱锥中，底面是正方形，侧棱，，是的中点，作交于点 D C A B P F E ‎ (1) 证明：；‎ ‎ (2) 证明：.‎ ‎ ‎ ‎20．（本小题满分10分）‎ ‎ 已知函数，其中a是常数.‎ ‎(1)当时，求的单调区间；‎ ‎ (2) 设,当时，试求函数的定义域并判断其奇偶性；‎ ‎(3)若对任意的恒有，试确定a的取值范围.‎ 长春三中2018—2019学年度高一上学期月考答案 一、 选择题：本题共12小题，每小题5分，共60分，在每小题给出的四个选项中只有一个选项是符合题目要求的．‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 A C D B C B C C A A D B 二、 填空题：本题共4小题，每小题5分共20分，把答案填在答题纸中的横线上 ‎13.(4,2)‎ ‎14. ‎ ‎15．‎ ‎ 16. ‎ 三、解答题（本大题4小题，共40分，解答应写出文字说明，证明过程或演算步骤）‎ ‎17. （本小题10分） ‎ ‎（1）………2‎ ‎（2）……..4‎ ‎（3）……4‎ ‎18. （本小题10分）‎ 解：(1)…….5‎ ‎（2）………5‎ ‎19.（本小题10分）‎ ‎(1)连结交于，连结。‎ 因为底面是矩形，所以点是的中点。‎ 又因为是的中点，所以在中，为中位线，所以。‎ 而平面，平面，所以平面。‎ ‎(2)由底面，得。‎ 因为底面是矩形，所以，所以平面。‎ 而平面，所以。‎ 因为，是的中点，所以是等腰三角形，。‎ 由和得平面。‎ 而平面，所以。‎ 又且，所以平面。‎ ‎20．解　(1)由得 定义域为{x| }，‎ 为减函数，为增函数 的减区间为 ‎ (2)定义域为（-2,2）‎ 所以为偶函数 ‎(3)由题意 则恒成立 ‎ ‎