数学卷·2018届湖北省宜昌市长阳一中高二上学期期中数学试卷（理科）（解析版）

数学卷·2018届湖北省宜昌市长阳一中高二上学期期中数学试卷（理科）（解析版）

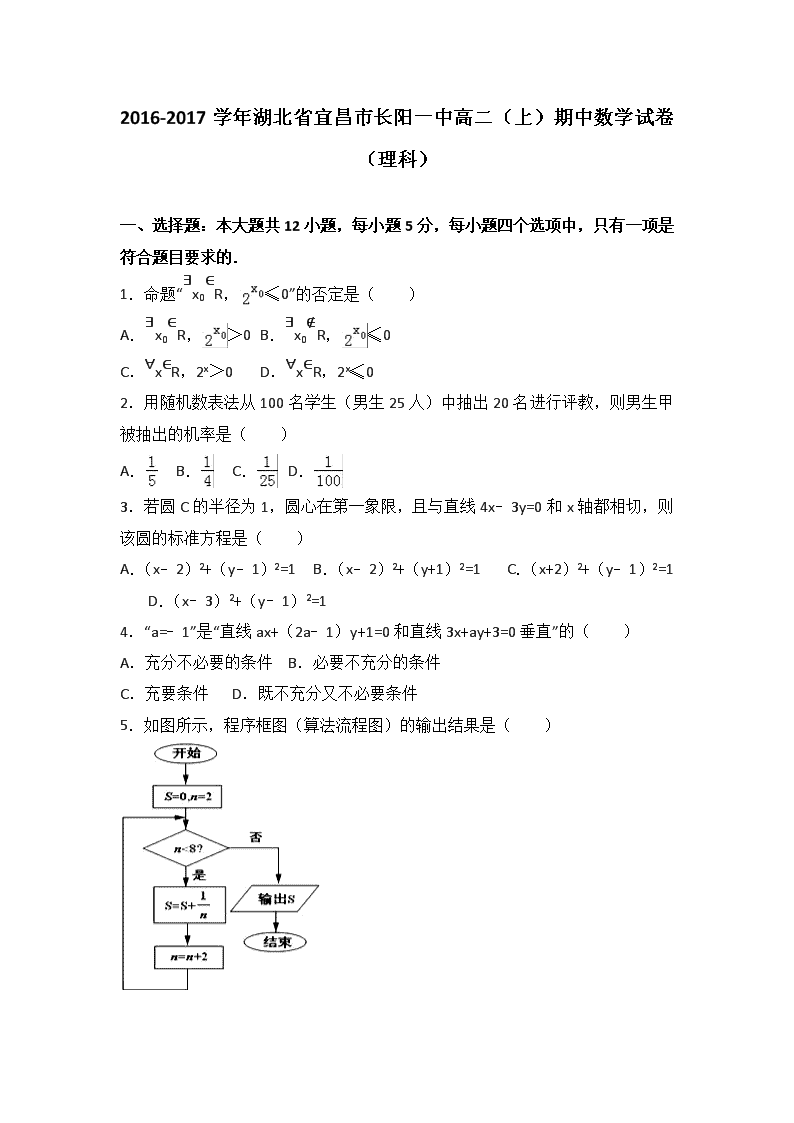
2016-2017 学年湖北省宜昌市长阳一中高二（上）期中数学试卷 （理科） 　 一、选择题：本大题共 12 小题，每小题 5 分，每小题四个选项中，只有一项是 符合题目要求的． 1．命题“∃x0∈R， ≤0”的否定是（　　） A．∃x0∈R， ＞0 B．∃x0∉R， ≤0 C．∀x∈R，2x＞0 D．∀x∈R，2x≤0 2．用随机数表法从 100 名学生（男生 25 人）中抽出 20 名进行评教，则男生甲 被抽出的机率是（　　） A． B． C． D． 3．若圆 C 的半径为 1，圆心在第一象限，且与直线 4x﹣3y=0 和 x 轴都相切，则 该圆的标准方程是（　　） A．（x﹣2）2+（y﹣1）2=1 B．（x﹣2）2+（y+1）2=1 C．（x+2）2+（y﹣1）2=1 D．（x﹣3）2+（y﹣1）2=1 4．“a=﹣1”是“直线 ax+（2a﹣1）y+1=0 和直线 3x+ay+3=0 垂直”的（　　） A．充分不必要的条件 B．必要不充分的条件 C．充要条件 D．既不充分又不必要条件 5．如图所示，程序框图（算法流程图）的输出结果是（　　） A． B． C． D． 6．直线 y=kx+3 与圆（x﹣2）2+（y﹣3）2=4 相交于 M，N 两点，若 ， 则 k 的取值范围是（　　） A． B． C． D． 7．从某高中随机选取 5 名高三男生，其身高和体重的数据如表所示： 身高 x（cm） 160 165 170 175 180 体重 y（kx） 63 66 70 72 74 根据上表可得回归直线方程 ，据此模型预报身高为 172cm 的高三男生 的体重为（　　） A．70.09 kg B．70.12 kg C．70.55 kg D．71.05 kg 8．已知 F1，F2 是椭圆的两个焦点，过 F1 且与椭圆长轴垂直的直线交椭圆于 A，B 两点，若△ABF2 是正三角形，则这个椭圆的离心率是（　　） A． B． C． D． 9．若直线 y=kx﹣k 交抛物线 y2=4x 于 A，B 两点，且线段 AB 中点到 y 轴的距离 为 3，则|AB|=（　　） A．12 B．10 C．8 D．6 10．一块石材表示的几何体的三视图如图所示，将该石材切削、打磨，加工成球， 则能得到的最大球的半径等于（　　） A．1 B．2 C．3 D．4 11．抛物线 y=x2 上的点到直线 2x﹣y=4 的最短距离是（　　） A． B． C． D． 12．已知 F1、F2 分别是双曲线 ﹣ =1（a＞0，b＞0）的左、右焦点，以坐标 原点 O 为圆心，OF1 为半径的圆与双曲线在第一象限的交点为 P，则当△PF1F2 的 面积等于 a2 时，双曲线的离心率为（　　） A． B． C． D．2 　 二、填空题：本大题共 4 小题，每小题 5 分，把答案填在相应题号后的横线 上． 13．将二进制数 110101（2）转化为十进制数为　　． 14．如图，正方形 ABCD 所在平面与正方形 ABEF 所在平面成 60°的二面角，则异 面直线 AD 与 BF 所成角的余弦值是　　． 15．甲、乙两人约定在 10：00﹣﹣﹣12：00 会面商谈事情，约定先到者应等另 一个人 30 分钟，即可离去，求两人能会面的概率　　（用最简分数表示）． 16．已知关于 x，y 的方程组 有两组不同的解，则实数 m 的取值 范围是　　． 　 三、解答题：本大题共 6 小题，解答应写出文字说明、证明过程或演算步骤． 17．命题 p：关于 x 的不等式 x2+2ax+4＞0 对一切 x∈R 恒成立，q：函数 f（x）= （3﹣2a）x 是增函数．若 p∨q 为真，p∧q 为假．求实数 a 的取值范围． 18．某高校 2011 年的自主招生考试成绩中随机抽取 100 名学生的笔试成绩，按 成绩分组：第 1 组[160，165），第 2 组[165，170），第 3 组[170，175），第 4 组[175，180），第 5 组[180，185）得到的频率分布直方图如图所示． （1）求第 3、4、5 组的频率并估计这次考试成绩的众数； （2）为了能选拔出最优秀的学生，该校决定在笔试成绩高的第 3、4、5 组中用 分层抽样抽取 6 名学生进入第二轮面试，求第 3、4、5 组每组各抽取多少名学生 进入第二轮面试？ （3）在（2）的前提下，学校决定在这 6 名学生中随机抽取 2 名学生接受甲考官 的面试，求：第 4 组至少有一名学生被甲考官面试的概率？ 19．在正方体 ABCD﹣A1B1C1D1 中，设 E 是棱 CC1 的中点． （1）求证：BD⊥AE （2）求证：AC∥平面 B1DE； （3）求锐二面角 E﹣BD﹣C 的余弦值． 20．如表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量 x（吨） 与相应的生产能耗 y（吨标准煤）的几组对照数据 x 3 4 5 6 y 2.5 3.5 4 5 （1）请根据上表提供的数据，用最小二乘法求出 y 关于 x 的线性回归方程 = x+ ； （2）已知该厂技术改造前 100 吨甲产品能耗为 90 吨标准煤．试根据（2）求出 的线性回归方程，预测生产 100 吨甲产品的生产能耗比技术改造前降低多少吨标 准煤？ 21．已知圆 O：x2+y2=2，直线 l：y=kx﹣2． （1）若直线 l 与圆 O 交于不同的两点 A、B，当∠AOB 为锐角时，求 k 的取值范 围． （2）若 ，P 是直线 l 上的动点，过 P 作圆 O 的两条切线 PC、PD，切点为 C、 D，探究：直线 CD 是否过定点． 22．已知椭圆 C1： + =1（a＞b＞0）经过点（1，e），其中 e 是椭圆 C1 的离 心率，以原点 O 为圆心，以椭圆 C1 的长轴长为直径的圆 C2 与直线 x﹣y+2=0 相 切． （Ⅰ）求椭圆 C1 和圆 C2 的方程； （Ⅱ）过椭圆 C1 的右焦点 F 的直线 l1 与椭圆 C1 交于点 A，B，过 F 且与直线 l1 垂 直的直线 l2 与圆 C2 交于点 C，D，以 A，B，C，D 为顶点的四边形的面积记为 S， 求 S 的取值范围． 　 2016-2017 学年湖北省宜昌市长阳一中高二（上）期中数 学试卷（理科） 参考答案与试题解析 　 一、选择题：本大题共 12 小题，每小题 5 分，每小题四个选项中，只有一项是 符合题目要求的． 1．命题“∃x0∈R， ≤0”的否定是（　　） A．∃x0∈R， ＞0 B．∃x0∉R， ≤0 C．∀x∈R，2x＞0 D．∀x∈R，2x≤0 【考点】命题的否定． 【分析】根据特称命题的否定是全称命题，即可得到结论． 【解答】解：命题是特称命题， 则命题的否定是∀x∈R，2x＞0， 故选：C 　 2．用随机数表法从 100 名学生（男生 25 人）中抽出 20 名进行评教，则男生甲 被抽出的机率是（　　） A． B． C． D． 【考点】简单随机抽样． 【分析】由已知中，抽样的方法为随机数表法，则每个个体被抽中的概率是相等 的，将整体容量 100 及样本容量 20 代入即可得到答案． 【解答】解：由于共有 100 名学生，抽取 20 人， 故每一名学生被抽中的概率 P= = ， 故选 A． 　 3．若圆 C 的半径为 1，圆心在第一象限，且与直线 4x﹣3y=0 和 x 轴都相切，则 该圆的标准方程是（　　） A．（x﹣2）2+（y﹣1）2=1 B．（x﹣2）2+（y+1）2=1 C．（x+2）2+（y﹣1）2=1 D．（x﹣3）2+（y﹣1）2=1 【考点】圆的标准方程． 【分析】要求圆的标准方程，半径已知，只需找出圆心坐标，设出圆心坐标为 （a，b），由已知圆与直线 4x﹣3y=0 相切，可得圆心到直线的距离等于圆的半径， 可列出关于 a 与 b 的关系式，又圆与 x 轴相切，可知圆心纵坐标的绝对值等于圆 的半径即|b|等于半径 1，由圆心在第一象限可知 b 等于圆的半径，确定出 b 的 值，把 b 的值代入求出的 a 与 b 的关系式中，求出 a 的值，从而确定出圆心坐标， 根据圆心坐标和圆的半径写出圆的标准方程即可． 【解答】解：设圆心坐标为（a，b）（a＞0，b＞0）， 由圆与直线 4x﹣3y=0 相切，可得圆心到直线的距离 d= =r=1， 化简得：|4a﹣3b|=5①， 又圆与 x 轴相切，可得|b|=r=1，解得 b=1 或 b=﹣1（舍去）， 把 b=1 代入①得：4a﹣3=5 或 4a﹣3=﹣5，解得 a=2 或 a=﹣ （舍去）， ∴圆心坐标为（2，1）， 则圆的标准方程为：（x﹣2）2+（y﹣1）2=1． 故选：A 　 4．“a=﹣1”是“直线 ax+（2a﹣1）y+1=0 和直线 3x+ay+3=0 垂直”的（　　） A．充分不必要的条件 B．必要不充分的条件 C．充要条件 D．既不充分又不必要条件 【考点】两条直线垂直的判定． 【分析】当 a=﹣1 时直线 ax+（2a﹣1）y+1=0 的斜率和直线 3x+ay+3=0 的斜率都 存在，只要看是否满足 k1•k2=﹣1 即可． 【解答】解：当a=﹣1 时直线 ax+（2a﹣1）y+1=0 的斜率是 ，直线 3x+ay+3=0 的斜率是 3， ∴满足 k1•k2=﹣1 a=0 时，直线 ax+（2a﹣1）y+1=0 和直线 3x+ay+3=0 垂直， ∴a=﹣1 是直线 ax+（2a﹣1）y+1=0 和直线 3x+ay+3=0 垂直的充分条件． 故选 A． 　 5．如图所示，程序框图（算法流程图）的输出结果是（　　） A． B． C． D． 【考点】程序框图． 【分析】模拟程序图框的运行过程，得出当n=8 时，不再运行循环体，直接输出 S 值． 【解答】解：模拟程序图框的运行过程，得； 该程序运行后输出的是计算 S= + + = ． 故选：D． 　 6．直线 y=kx+3 与圆（x﹣2）2+（y﹣3）2=4 相交于 M，N 两点，若 ， 则 k 的取值范围是（　　） A． B． C． D． 【考点】直线和圆的方程的应用． 【分析】直线与圆相交，有两个公共点，设弦长为L，弦心距为 d，半径为 r，则 可构建直角三角形，从而将问题仍然转化为点线距离问题． 【解答】解：圆（x﹣2）2+（y﹣3）2=4 的圆心为（2，3），半径等于 2， 圆心到直线 y=kx+3 的距离等于 d= 由弦长公式得 MN=2 ≥2 ， ∴ ≤1， 解得 ， 故选 B． 　 7．从某高中随机选取 5 名高三男生，其身高和体重的数据如表所示： 身高 x（cm） 160 165 170 175 180 体重 y（kx） 63 66 70 72 74 根据上表可得回归直线方程 ，据此模型预报身高为 172cm 的高三男生 的体重为（　　） A．70.09 kg B．70.12 kg C．70.55 kg D．71.05 kg 【考点】线性回归方程． 【分析】根据所给的表格做出本组数据的样本中心点，根据样本中心点在线性回 归直线上，利用待定系数法做出 的值，现在方程是一个确定的方程，根据所给 的 x 的值，代入线性回归方程，预报身高为 172cm 的高三男生的体重 【解答】解：由表中数据可得 = =170 = =69 ∵（ ， ）一定在回归直线方程 上 故 69=0.56×170+ 解得 =﹣26.2 故 当 x=172 时， =70.12 故选 B 　 8．已知 F1，F2 是椭圆的两个焦点，过 F1 且与椭圆长轴垂直的直线交椭圆于 A，B 两点，若△ABF2 是正三角形，则这个椭圆的离心率是（　　） A． B． C． D． 【考点】椭圆的应用；椭圆的简单性质． 【分析】由△ABF2 是正三角形可知 ，即 ，由此推 导出这个椭圆的离心率． 【解答】解：由题 ，∴ 即 ∴ ， ∴ ， 解之得： （负值舍去）． 故答案选 A． 　 9．若直线 y=kx﹣k 交抛物线 y2=4x 于 A，B 两点，且线段 AB 中点到 y 轴的距离 为 3，则|AB|=（　　） A．12 B．10 C．8 D．6 【考点】直线与圆锥曲线的关系． 【分析】根据抛物线的方程求出准线方程，利用抛物线的定义抛物线上的点到焦 点的距离等于到准线的距离，列出方程求出 A，B 的中点横坐标，求出线段 AB 的中点到 y 轴的距离． 【解答】解：直线 y=kx﹣k 恒过（1，0），恰好是抛物线 y2=4x 的焦点坐标， 设 A（x1，y1） B（x2，y2） 抛物 y2=4x 的线准线 x=﹣1，线段 AB 中点到 y 轴的距离为 3，x1+x2=6， ∴|AB|=|AF|+|BF|=x1+x2+2=8， 故选：C． 　 10．一块石材表示的几何体的三视图如图所示，将该石材切削、打磨，加工成球， 则能得到的最大球的半径等于（　　） A．1 B．2 C．3 D．4 【考点】球内接多面体；由三视图求面积、体积；球的体积和表面积． 【分析】由题意，该几何体为三棱柱，所以最大球的半径为正视图直角三角形内 切圆的半径 r． 【解答】解：由题意，该几何体为三棱柱，所以最大球的半径为正视图直角三角 形内切圆的半径 r，则 8﹣r+6﹣r= ， ∴r=2． 故选：B． 　 11．抛物线 y=x2 上的点到直线 2x﹣y=4 的最短距离是（　　） A． B． C． D． 【考点】直线与圆锥曲线的关系． 【分析】利用点到直线的距离公式，结合配方法，即可得到结论． 【解答】解：设抛物线 y=x2 上的点的坐标为（x，y），则 由点到直线的距离公式可得 d= = = ≥ ∴抛物线 y=x2 上的点到直线 2x﹣y=4 的最短距离是 故选 B． 　 12．已知 F1、F2 分别是双曲线 ﹣ =1（a＞0，b＞0）的左、右焦点，以坐标 原点 O 为圆心，OF1 为半径的圆与双曲线在第一象限的交点为 P，则当△PF1F2 的 面积等于 a2 时，双曲线的离心率为（　　） A． B． C． D．2 【考点】双曲线的简单性质． 【分析】先设 F1F2=2c，由题意知△F1F2P 是直角三角形，进而在 RT△PF1F2 中结 合双曲线的定义和△PF1F2 的面积，进而根据双曲线的简单性质求得 a，c 之间的 关系，则双曲线的离心率可得． 【解答】解：设 F1F2=2c，由题意知△F1F2P 是直角三角形， ∴F1P2+F2P2=F1F22， 又根据曲线的定义得： F1P﹣F2P=2a， 平方得：F1P2+F2P2﹣2F1P×F2P=4a2 从而得出 F1F22﹣2F1P×F2P=4a2 ∴F1P×F2P=2（c2﹣a2） 又当△PF1F2 的面积等于 a2 即 F1P×F2P=a2 2（c2﹣a2）=a2 ∴c= a， ∴双曲线的离心率 e= = ． 故选 A． 　 二、填空题：本大题共 4 小题，每小题 5 分，把答案填在相应题号后的横线 上． 13．将二进制数 110101（2）转化为十进制数为　53　． 【考点】整除的定义． 【分析】二进制转换为十进制方法：按权相加法，即将二进制每位上的数乘以权 （即该数位上的 1 表示 2 的多少次方），然后相加之和即是十进制数，据此解答 即可． 【解答】解：110101（2）=1+1×22+1×24+1×25=53 故答案为：53． 　 14．如图，正方形 ABCD 所在平面与正方形 ABEF 所在平面成 60°的二面角，则异 面直线 AD 与 BF 所成角的余弦值是　 　． 【考点】异面直线及其所成的角． 【分析】由题意得，CB⊥AB，AB⊥BE．可得正方形 ABCD 所在平面与正方形 ABEF 的二面角即∠CBE=60°，同时也得 AB⊥平面 BCE，即 AB⊥CE，即是 EF⊥CE．进 而求出 CF、FB、BC，即可求出异面直线 AD 与 BF 所成角的余弦值． 【解答】解：由题意得，CB⊥AB，AB⊥BE．可得正方形 ABCD 所在平面与正方 形 ABEF 的二面角即∠CBE=60°， 同时也得 AB⊥平面 BCE，即 AB⊥CE， 即三角形 CEF 为直角三角形和三角形 CBE 为等边三角形； 即是 EF⊥CE．设 AB=1，则 CE=1，CF= ，FB= ， 利用余弦定理，得 ． 故异面直线 AD 与 BF 所成角的余弦值是 ． 　 15．甲、乙两人约定在 10：00﹣﹣﹣12：00 会面商谈事情，约定先到者应等另 一个人 30 分钟，即可离去，求两人能会面的概率　 　（用最简分数表示）． 【考点】几何概型． 【分析】由题意知本题是一个几何概型，试验包含的所有事件是 Ω={（x，y）|0 ＜x＜2，0＜y＜2}，做出事件对应的集合表示的面积，写出满足条件的事件是 A={（x，y）|0＜x＜0，0＜y＜2，|x﹣y|≤ }，算出事件对应的集合表示的面积， 根据几何概型概率公式得到结果． 【解答】解：由题意知本题是一个几何概型，设事件 A 为“两人能会面”， 试验包含的所有事件是 Ω={（x，y）|0＜x＜2，0＜y＜2}，并且事件对应的集合 表示的面积是 s=4， 满足条件的事件是 A={（x，y）|0＜x＜0，0＜y＜2，|x﹣y|≤ } 所以事件对应的集合表示的图中阴影部分，其面积是 4﹣2× × × = ， 根据几何概型概率公式得到 P= ， 故答案为： 　 16．已知关于 x，y 的方程组 有两组不同的解，则实数 m 的取值 范围是　[0，﹣1+ ）　． 【考点】直线与圆的位置关系． 【分析】关于 x，y 的方程组 有两组不同的解，则表示两个方程 对应的曲线有两个不同的交点，从而可得满足条件的实数 m 的取值范围． 【解答】解：方程 y= 可化为（x+1）2+y2=1（y≥0） 表示圆心为（﹣1，0）、半径为 1 的圆 x 轴以上部分（含于 x 轴交点）． 设直线 x+y﹣m=0 与圆相切，则 =1， ∴m=﹣1± 直线 x+y﹣m=0 过原点时，m=0， ∴关于 x，y 的方程组 有两组不同的解时，m∈[0，﹣1+ ）． 故答案为：[0，﹣1+ ）． 　 三、解答题：本大题共 6 小题，解答应写出文字说明、证明过程或演算步骤． 17．命题 p：关于 x 的不等式 x2+2ax+4＞0 对一切 x∈R 恒成立，q：函数 f（x）= （3﹣2a）x 是增函数．若 p∨q 为真，p∧q 为假．求实数 a 的取值范围． 【考点】复合命题的真假． 【分析】由 p：关于 x 的不等式 x2+2ax+4＞0 对一切 x∈R 恒成立，q：函数 f（x） =（3﹣2a）x 是增函数分别列示求出 a 的范围，再由于 p 或 q 为真，p 且 q 为假， 可知 p 和 q 一真一假，分类求出 a 的范围，取并集得答案． 【解答】解：设g（x）=x2+2ax+4，由于关于 x 的不等式 x2+2ax+4＞0 对一切 x∈R 恒成立， ∴函数 g（x）的图象开口向上且与 x 轴没有交点， 故△=4a2﹣16＜0，∴﹣2＜a＜2． 又∵函数 f（x）=（3﹣2a）x 是增函数， ∴3﹣2a＞1，得 a＜1． 又由于 p 或 q 为真，p 且 q 为假，可知 p 和 q 一真一假． （1）若 p 真 q 假，则 ，得 1≤a＜2； （2）若 p 假 q 真，则 ，得 a≤﹣2． 综上可知，所求实数 a 的取值范围为 1≤a＜2，或 a≤﹣2． 　 18．某高校 2011 年的自主招生考试成绩中随机抽取 100 名学生的笔试成绩，按 成绩分组：第 1 组[160，165），第 2 组[165，170），第 3 组[170，175），第 4 组[175，180），第 5 组[180，185）得到的频率分布直方图如图所示． （1）求第 3、4、5 组的频率并估计这次考试成绩的众数； （2）为了能选拔出最优秀的学生，该校决定在笔试成绩高的第 3、4、5 组中用 分层抽样抽取 6 名学生进入第二轮面试，求第 3、4、5 组每组各抽取多少名学生 进入第二轮面试？ （3）在（2）的前提下，学校决定在这 6 名学生中随机抽取 2 名学生接受甲考官 的面试，求：第 4 组至少有一名学生被甲考官面试的概率？ 【考点】等可能事件的概率；分层抽样方法；众数、中位数、平均数． 【分析】（1）利用频率等于频数乘以组距得到各组的频率，根据众数是直方图中 最高矩形的底边中点的坐标，求出众数的估计值． （2）利用频数等于频率乘以样本容量得到，第 3，4，5 组共有 60 名学生，利用 各组的人数与样本容量的比乘以 60 得到每组抽取的人数． （3）列举出从六位同学中抽两位同学的所有的抽法，列举出第 4 组的 2 位同学 为 B1，B2，至少有一位同学入选的抽法，由古典概型的概率公式求出概率． 【解答】解：（1）由题设可知，第 3 组的频率为 0.06×5=0.3； 第 4 组的频率为 0.04×5=0.2 第 5 组的频率为 0.02×5=0.1．… 估计这次考试成绩的众数为 167．．… （2）第三组的人数为 0.3×100=30 人； 第四组的人数为 0.2×100=20 人； 第五组的人数为 0.1×100=10 人； 因为第 3，4，5 组共有 60 名学生，所以利用分层抽样在 60 名学生中抽取 6 名学 生，每组抽取的人数分别为： 第 3 组抽 30× =3 人； … 第 4 组抽 20× =2 人； … 第 5 组抽 10× =1 人； … 所以第 3，4，5 组分别抽取出 3 人，2 人和 1 人．… （3）设第 3 组的 3 位同学为 A1，A2，A3，第 4 组的两位同学为 B1，B2， 第 5 组的 1 位同学为 C1，… 则从六位同学中抽两位同学有：（A1，A2），（A1，A3），（A1，B1），（A1，B2）， （A1，C1），（A2，A3），（A2，B1）（A2，B2），（A2，C1），（A3，B1）， （A3，B2），（A3，C1），（B1，B2），（B1，C1），（B2，C1） 共 15 种可能．… 其中第 4 组的 2 位同学为 B1，B2，至少有一位同学入选的有（A1，B1），（A1， B2），（A2，B1）（A2，B2），（A3，B1），（A3，B2），（B1，B2），（B1，C1），（B2，C1） 共 9 种可能… 所以第 4 组至少有一名学生被甲考官面试的概率为 ．…． 　 19．在正方体 ABCD﹣A1B1C1D1 中，设 E 是棱 CC1 的中点． （1）求证：BD⊥AE （2）求证：AC∥平面 B1DE； （3）求锐二面角 E﹣BD﹣C 的余弦值． 【考点】二面角的平面角及求法；直线与平面平行的判定． 【分析】（1）连接 BD，AE，推导出 BD⊥AC，EC⊥BD，由此能证明 BD⊥AE． （2）连接 AC1，设 AC1∩B1D=G，连接 GE，则 AC∥GE，由此能证明 AC∥平面 B1DE． （3）连结 DE、BE，取 BD 中点 O，连结 EO，CO，则 EO⊥BD，CO⊥BD，∠EOC 是二面角 E﹣BD﹣C 的平面角，由此能求出二面角 E﹣BD﹣C 的余弦值． 【解答】证明：（1）连接 BD，AE， ∵四边形 ABCD 为正方形，∴BD⊥AC， ∵E 是棱 CC1 的中点，∴EC⊥底面 ABCD， ∵BD⊂面 ABCD，∴EC⊥BD， 又 EC∩AC=C，∴BD⊥平面 AEC， ∵AE⊂平面 AEC，∴BD⊥AE． （2）连接 AC1，设 AC1∩B1D=G，连接 GE， 则 G 为 AC1 中点，而 E 为 C1C 的中点， ∴GE 为三角形 ACC1 的中位线，∴AC∥GE， ∵GE⊂平面 B1DE，AC⊄平面 B1DE， ∴AC∥平面 B1DE． 解：（3）连结 DE、BE， 设正方体 ABCD﹣A1B1C1D1 中棱长为 2， 则 CE=1，DE=BE= = ， 取 BD 中点 O，连结 EO，CO，则 EO⊥BD，CO⊥BD， ∴∠EOC 是二面角 E﹣BD﹣C 的平面角， OC= = ， ∴OE= = ， ∴cos∠EOC= = ． ∴二面角 E﹣BD﹣C 的余弦值为 ． 　 20．如表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量 x（吨） 与相应的生产能耗 y（吨标准煤）的几组对照数据 x 3 4 5 6 y 2.5 3.5 4 5 （1）请根据上表提供的数据，用最小二乘法求出 y 关于 x 的线性回归方程 = x+ ； （2）已知该厂技术改造前 100 吨甲产品能耗为 90 吨标准煤．试根据（2）求出 的线性回归方程，预测生产 100 吨甲产品的生产能耗比技术改造前降低多少吨标 准煤？ 【考点】线性回归方程． 【分析】（1）根据所给的这组数据求出利用最小二乘法所需要的几个数据，代入 求系数 b 的公式，求得结果，再把样本中心点代入，求出 的值，得到线性回归 方程． （2）根据上一问所求的线性回归方程，把 x=100 代入线性回归方程，预测生产 100 吨甲产品的生产能耗比技改前降低标准煤的数量． 【解答】解：（1）由对照数据，计算得 =4.5， =3.5， ∴ = =0.8 ∴ =0.15， ∴所求线性回归方程为 =0.8x+0.15； （2）由（1）求出的线性回归方程，预测生产 100 吨甲产品的生产能耗比技改前 降低 90﹣（0.8×100+0.15）=9.85（吨）． 　 21．已知圆 O：x2+y2=2，直线 l：y=kx﹣2． （1）若直线 l 与圆 O 交于不同的两点 A、B，当∠AOB 为锐角时，求 k 的取值范 围． （2）若 ，P 是直线 l 上的动点，过 P 作圆 O 的两条切线 PC、PD，切点为 C、 D，探究：直线 CD 是否过定点． 【考点】直线与圆的位置关系． 【 分 析 】（1 ） 利 用 点 到 直 线 的 距 离 公 式 ， 结 合 点 O 到 l 的 距 离 ，可求 k 的值； （2）由题意可知：O、P、C、D 四点共圆且在以 OP 为直径的圆上，C、D 在圆 O：x2+y2=2 上可得直线 C，D 的方程，即可求得直线 CD 是否过定点 【解答】解：（1）由题意， ， ∴ 或 1 ； （2）由题意可知：O、P、C、D 四点共圆且在以 OP 为直径的圆上， 设 P（t， ），其方程为： ， 又 C、D 在圆 O：x2+y2=2 上 ∴lCD： ， 即 由 ，得 ， ∴直线 CD 过定点（ ，﹣1）． 　 22．已知椭圆 C1： + =1（a＞b＞0）经过点（1，e），其中 e 是椭圆 C1 的离 心率，以原点 O 为圆心，以椭圆 C1 的长轴长为直径的圆 C2 与直线 x﹣y+2=0 相 切． （Ⅰ）求椭圆 C1 和圆 C2 的方程； （Ⅱ）过椭圆 C1 的右焦点 F 的直线 l1 与椭圆 C1 交于点 A，B，过 F 且与直线 l1 垂 直的直线 l2 与圆 C2 交于点 C，D，以 A，B，C，D 为顶点的四边形的面积记为 S， 求 S 的取值范围． 【考点】直线与圆锥曲线的综合问题；椭圆的标准方程． 【分析】（Ⅰ）由椭圆经过点（1，e），以原点 O 为圆心，以椭圆 C1 的长轴长为 直径的圆 C2 与直线 x﹣y+2=0 相切，列出方程组求出 a，b，由此能求出椭圆 C1 的方程和圆 C2 的方程． （Ⅱ）若直线 AB 的斜率不存在，由 l1⊥l2，得 S=2；若直线 AB 的斜率为 0，由 l1 ⊥l2，得|AB|=2 ，|CD|=2，S= ；若直线 AB 的斜率存在且不为 0 ， 设 l1 的 方 程 为 y=k （ x﹣1 ）， 联 立 ， 得 （ 1+2k2 ） x2﹣4k2x+2k2﹣2=0，由此利用韦达定理、根的差别式、弦长公式、函数的单调性， 结合已知条件能求出 S 的取值范围． 【解答】解：（Ⅰ）∵椭圆 C1： + =1（a＞b＞0）经过点（1，e）， 以原点 O 为圆心，以椭圆 C1 的长轴长为直径的圆 C2 与直线 x﹣y+2=0 相切， ∴由已知得 ，解得 a= ，b=1． 所以椭圆 C1 的方程为 ，圆 C2 的方程为 x2+y2=2． （Ⅱ）若直线 AB 的斜率不存在，由 l1⊥l2，得|AB|= = ，|CD|=2 ， 此时 S= ． 若直线 AB 的斜率为 0，由 l1⊥l2，得|AB|=2 ，|CD|=2 =2， 此时 S= ． 若直线 AB 的斜率存在且不为 0，设 l1 的方程为 y=k（x﹣1）． 设 A（x1，x2），B（x2，y2），则 ， 消 y，得（1+2k2）x2﹣4k2x+2k2﹣2=0， 所以 ， ， △=16k4﹣4（1+2k2）（2k2﹣2）=8k2+8＞0． |AB|= = = = ． 又 l2 的方程为 y=﹣ （x﹣1），即 x+ky﹣1=0， 得|CD|=2 =2 ． 所以 S= |AB|×|CD|= =2 ． 因为 k2＞0，关于 k2 是单调递减函数， ∈（2，2 ）． 综上得，S 的取值范围是[2，2 ]．