上海市浦东新区2013届高三下学期4月高考预测数学理试题

上海市浦东新区2013届高三下学期4月高考预测数学理试题

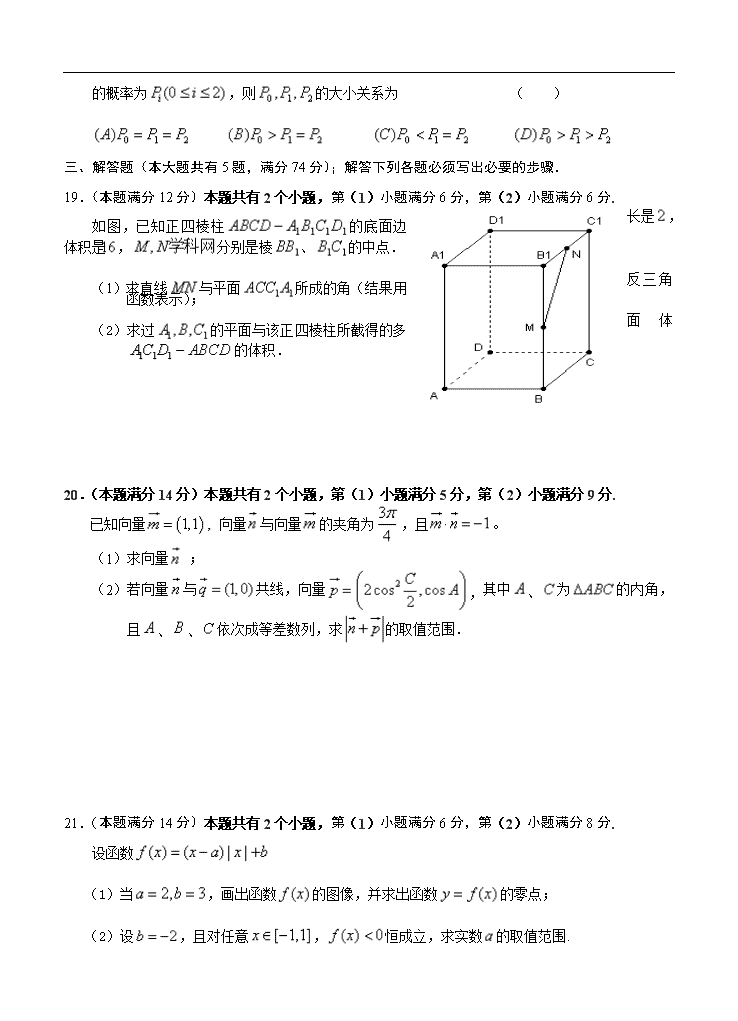
上海市浦东新区2013届高三下学期4月高考预测 数学理试题 注意：1. 答卷前，考生务必在答题纸上指定位置将姓名、学校、考号填写清楚.‎ ‎ 2. 本试卷共有23道试题，满分150分，考试时间120分钟.‎ 一、填空题（本大题满分56分，每小题4分）；本大题共有14小题，考生应在答题纸相应编号的空格内直接填写结果，每个空格填对得4分，否则一律得零分.‎ ‎1．已知复数满足（其中i为虚数单位），则= .‎ ‎2．已知集合A＝，B＝，且，则实数a的值是 .‎ ‎3．某学校高一、高二、高三年级的学生人数之比为，现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本，则应从高二年级抽取 名学生.‎ ‎4．函数与的图像关于直线对称，则 .‎ ‎5．把三阶行列式中第1行第3列元素的代数余子式记为，则关于 的不等式的解集为 . ‎ ‎6．若双曲线的渐近线方程为，它的一个焦点是，则双曲线的标准方程是 .‎ ‎7．若直线与圆有公共点，则实数的取值范围是 .‎ ‎8．记直线：（）与坐标轴所围成的直角三角形的面积为，则 .‎ ‎9．在中，角A、B、C所对的边分别为、、，若，则 .‎ ‎10．若等式对一切都成立，其中，，，…，为实常数，则＝ .‎ ‎11．方程在区间上解的个数为 . ‎ ‎12．某人从标有1、2、3、4的四张卡片中任意抽取两张.约定如下：如果出现两个偶数或两个奇数，就将两数相加的和记为；如果出现一奇一偶，则将它们的差的绝对值记为，则随机变量的数学期望为 .‎ ‎13．如果是函数图像上的点，是函数图像上的点，且两点之间的距离 能取到最小值，那么将称为函数与之间的距离.按这个定义，函数和之间的距离是 .‎ ‎14．数列满足（）．‎ ‎①存在可以生成的数列是常数数列；‎ ‎②“数列中存在某一项”是“数列为有穷数列”的充要条件；‎ ‎③若为单调递增数列，则的取值范围是；‎ ‎④只要，其中，则一定存在；‎ 其中正确命题的序号为 .‎ 二、选择题（本大题共有4题，满分20分）； 每小题都给出四个选项，其中有且只有一个选项是正确的，选对得 5分，否则一律得零分.‎ ‎15．“a＝‎1”‎是“直线l1：ax＋2y－1＝0与直线l2：x＋(a＋1)y＋4＝0平行”的 （ ）‎ 充分不必要条件 必要不充分条件 ‎ 充分必要条件 既不充分也不必要条件 ‎16．已知则与的夹角为 （ ）‎ ‎ ‎ ‎17．已知以为周期的函数，其中。若方程恰有5个实数解，则的取值范围为 （ ） ‎ ‎ ．‎ ‎18．从集合中任取3个元素组成一个集合，记中所有元素之和被3‎ 除余数为的概率为，则的大小关系为 （ ） ‎ ‎ ‎ 三、解答题（本大题共有5题，满分74分）；解答下列各题必须写出必要的步骤．‎ ‎19．（本题满分12分）本题共有2个小题，第（1）小题满分6分，第（2）小题满分6分.‎ 如图，已知正四棱柱的底面边长是，体积是，分别是棱、的中点．‎ ‎（1）求直线与平面所成的角（结果用反三角函数表示）；‎ ‎（2）求过的平面与该正四棱柱所截得的多面体的体积．‎ ‎20．（本题满分14分）本题共有2个小题，第（1）小题满分5分，第（2）小题满分9分.‎ 已知向量向量与向量的夹角为，且。‎ ‎（1）求向量 ； ‎ ‎（2）若向量与共线，向量，其中、为的内角，且、、依次成等差数列，求的取值范围．‎ ‎21．（本题满分14分）本题共有2个小题，第（1）小题满分6分，第（2）小题满分8分.‎ 设函数 ‎（1）当，画出函数的图像，并求出函数的零点；‎ ‎（2）设，且对任意，恒成立，求实数的取值范围.‎ ‎22．（本题满分16分）本题共有3个小题，第（1）小题满分4分，第（2）小题满分6分，第（3）小题满分6分.‎ 已知直角的三边长，满足 ‎（1）在之间插入2011个数，使这2013个数构成以为首项的等差数列，且它们的和为，求的最小值；‎ ‎（2）已知均为正整数，且成等差数列，将满足条件的三角形的面积从小到大排成一列，且，求满足不等式的所有的值；‎ ‎（3）已知成等比数列，若数列满足，证明：数列中的任意连续三项为边长均可以构成直角三角形，且是正整数.‎ ‎23．（本题满分18分）本题共有3个小题，第（1）小题满分4分，第（2）小题满分6分，第（3）小题满分8分.‎ ‎（1）设椭圆：与双曲线：有相同的焦点，是椭圆与双曲线的公共点，且的周长为，求椭圆的方程； ‎ 我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”.‎ x y o ‎3‎ ‎（2）如图，已知“盾圆”的方程为.设“盾圆”上的任意一点到的距离为，到直线的距离为，求证：为定值； ‎ ‎（3）由抛物线弧：（）与第（1）小题椭圆弧：（）所合成的封闭曲线为“盾圆”.设过点的直线与“盾圆”交于两点，，且（），试用 表示；并求的取值范围. ‎ ‎ ‎ 浦东新区2013年高考预测 数学试卷答案 一、填空题（本大题满分56分，每小题4分）；本大题共有14小题，考生应在答题纸相应编号的空格内直接填写结果，每个空格填对得4分，否则一律得零分.‎ ‎1．； 2．1； 3．20； 4．4； 5．； 6．； 7．；‎ ‎8．； 9．4； 10． 11．4； 12．‎ ‎13． 14．①④。‎ 二、选择题（本大题共有4题，满分20分）； 每小题都给出四个选项，其中有且只有一个选项是正确的，选对得 5分，否则一律得零分.‎ ‎15． ； 16． ； 17． 18． 。 ‎ 三、解答题（本大题共有5题，满分74分）；解答下列各题必须写出必要的步骤．‎ ‎19． 解：（1）连结，，‎ 直线与平面所成的角等于直线与平面所成的角.‎ 连结,连结，‎ 是直线与平面所成的角.……………………………2分 中，，…………………………………………4分 ‎.‎ 直线与平面所成的角等于.……………………6分 ‎（2）正四棱柱的底面边长是，体积是，‎ ‎.………………………………………………………………………8分 ‎；‎ ‎，……………………11分 多面体的体积为.……………………………………12分 ‎（文）（1）连结,，‎ 就是异面直线与所成角.…………………………………2分 在，………………………………4分 ‎，.‎ 所以异面直线与所成角为. …………………………6分 ‎20． 解：（1）设.由，得 ①………………………2分 又向量与向量的夹角为，得 ②……………………………4分 由①、②解得或，或.………………5分 ‎（2）向量与共线知；……………………………………………6分 由知.………………………7分 ‎， ……………………………8分 ‎…………………………9分 ‎.………11分 ‎，…………12分 得，即，…………………………13分 ‎.…………………………………………………………14分 ‎21．解：（1），………………………………………2分 画图正确.…………………………………………………………………………4分 当时，由，得，此时无实根；‎ 当时，由，得，得.‎ 所以函数的零点为.………………………………………………………6分 ‎（2）由＜0得，.‎ 当时，取任意实数，不等式恒成立.…………………………………8分 当时，.令，则在上单调递增，‎ ‎∴；……………………………………………………10分 当时，，令， ‎ 则在上单调递减，所以在上单调递减.‎ ‎∴ .…………………………………………………12分 ‎ 综合 .……………………………………………………………………14分 ‎（文）（2）当时，取任意实数，不等式恒成立；………………………8分 当时，，令，则在上单调递增，‎ ‎∴；……………………………………………………10分 当时，，令， ‎ 则在上单调递减，单调递增；‎ ‎∴.……………………………………………12分 综合 .……………………………………………………………………14分 ‎22．解：（1）是等差数列，∴，即.………2分 所以，的最小值为；……………………………4分 ‎（2）设的公差为，则……5分 设三角形的三边长为，面积，，‎ ‎.………………………………7分 由得， ‎ 当时，，‎ 经检验当时，，当时，.………9分 综上所述，满足不等式的所有的值为2、3、4.……………10分 ‎（3）证明：因为成等比数列，.‎ 由于为直角三角形的三边长，知，，………11分 又，得，‎ 于是 ‎.…………12分 ‎，则有.‎ 故数列中的任意连续三项为边长均可以构成直角三角形.……………14分 因为 ，‎ ‎，……………………………………………………15分 由，同理可得，‎ 故对于任意的都有是正整数.………………………………………16分 ‎（文）（2）设的公差为，则， .…5分 设三角形的三边长为，‎ 面积，，………………………………7分 当为偶数时，‎ ‎;‎ 当为奇数时，;……9分 综上，.……………………………………………………10分 ‎（3）证明：因为成等比数列，.………………………………………11分 由于为直角三角形的三边长，知，，………12分 又,得.……13分 于是 ‎.……………14分 ‎, 则有.……………………15分 故数列中的任意连续三项为边长均可以构成直角三角形.……………16分 ‎23． 解：（1）由的周长为得，‎ 椭圆与双曲线：有相同的焦点，所以，‎ 即，，椭圆的方程；…………………4分 ‎（2）证明：设“盾圆”上的任意一点的坐标为，.………5分 当时，，，‎ 即；…………………………7分 当时，，，‎ 即；…………………………9分 所以为定值；…………………………………………………………10分 ‎（3）显然“盾圆”由两部分合成，所以按在抛物线弧或椭圆弧上加以分类，由“盾圆”的对称性，不妨设在轴上方（或轴上）：‎ x y o 当时，，此时，；……………………11分 当时，在椭圆弧上， ‎ 由题设知代入得，‎ ‎，‎ 整理得，‎ 解得或（舍去）. …12分 当时在抛物线弧上， ‎ 由方程或定义均可得到，于是，‎ 综上，（）或（）；‎ 相应地，，…………………………………………14分 当时在抛物线弧上，在椭圆弧上，‎ ‎；……………………15分 当时在椭圆弧上，在抛物线弧上，‎ ‎；……………………16分 当时、在椭圆弧上，‎ ‎；…………………………17分 综上的取值范围是.…………………………………………………18分 ‎（文）（3）因为“盾圆”关于轴对称，设于是，‎ 所以面积，………………………………………………………11分 按点位置分2种情况：‎ ①当在抛物线弧（）上时，‎ 设所在的直线方程（），‎ 联立，得，同理， ‎ 面积，所以；………………14分 ②当在椭圆弧上时， ‎ 于是联立，得；‎ 即，由，‎ 当且仅当等号成立，所以，…………………………………17分 综上等腰面积的最大值为.…………………………………………18分