- 2021-06-23 发布 |
- 37.5 KB |
- 22页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
湖南省衡阳市2020届高三下学期第一次模拟考试数学(文)试题 Word版含解析
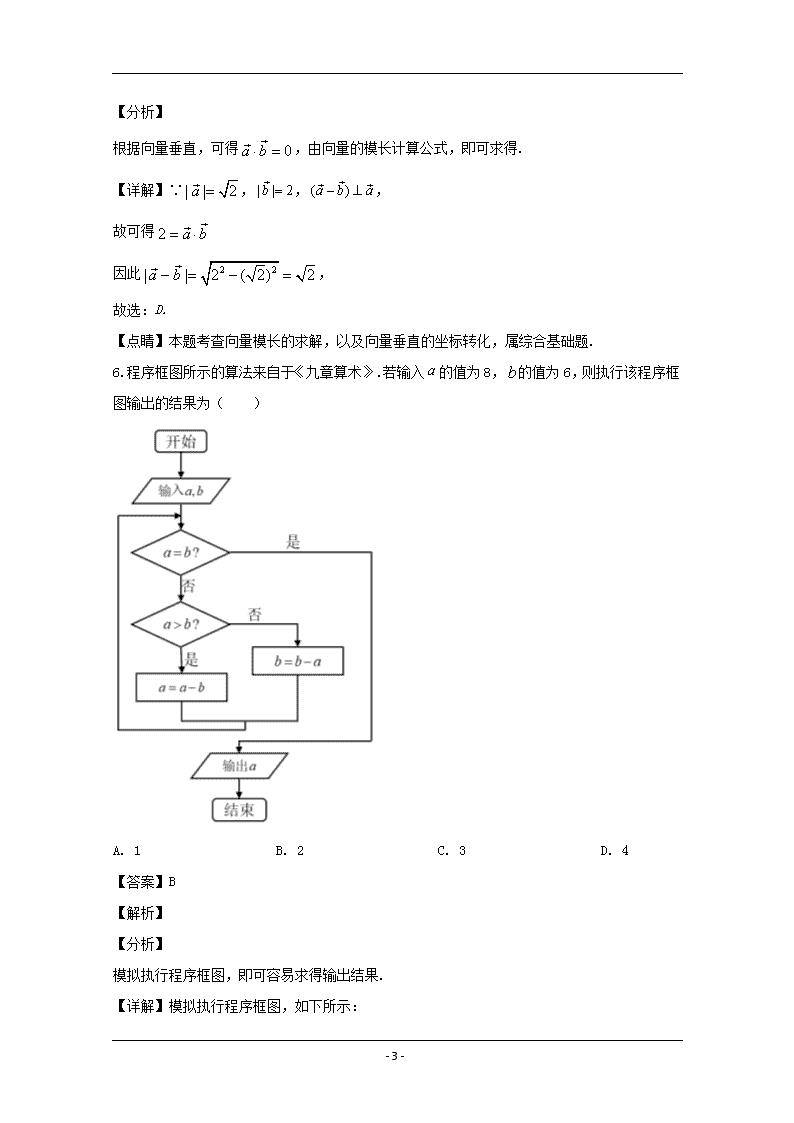
www.ks5u.com 湖南省衡阳市2020届高三第一次联考(一模) (文科)数学试题 第Ⅰ卷 一、选择题:本大题共12小题,每小题5分,满分60分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知集合,,则( ) A. B. C. D. 【答案】C 【解析】 【分析】 求解二次不等式和指数函数值域,解得集合,再求交集即可. 【详解】依题意,,,所以. 故选:C. 【点睛】本题考查二次不等式的求解,指数函数的值域,集合的交运算,属综合基础题. 2.在复平面内,复数所对应的点的坐标为,则的实部与虚部的和是( ) A. 2 B. 0 C. D. 【答案】B 【解析】 【分析】 根据题意,写出复数,则问题得解. 【详解】,所以复数的实部是1,虚部是,其和为0, 故选:B. 【点睛】本题考查由复数对应点的坐标写出复数,以及复数实部和虚部的辨识,属基础题. 3.已知,则、、的大小关系为( ) A. B. C. D. 【答案】A 【解析】 【分析】 - 22 - 根据对数函数和指数函数的单调性,即可容易判断. 【详解】∵,因此, 故选:A. 【点睛】本题考查利用指数函数和对数函数的单调性比较大小,属基础题. 4.研究机构对20岁至50岁人体脂肪百分比和年龄(岁)的关系进行了研究通过样本数据,求得回归方程现有下列说法: ①某人年龄为70岁,有较大的可能性估计他的体内脂肪含量约40.15%; ②年龄每增加一岁,人体脂肪百分比就增加0.45%; ③20岁至50岁人体脂肪百分比和年龄(岁)成正相关. 上述三种说法中正确的有( ) A. 3个 B. 2个 C. 1个 D. 0个 【答案】B 【解析】 【分析】 根据线性回归方程,结合选项进行逐一判断即可. 【详解】①令,可得,故①正确; ②因为线性回归方程的斜率为,故年龄每增加一岁,人体脂肪百分比就增加, 故②错误; ③因为线性回归方程的斜率为正数,故人体脂肪百分比和年龄(岁)成正相关, 故③正确. 故选:B. 【点睛】本题考查线性回归方程的辨识和理解,属基础题. 5.若,,且,则( ) A. B. 2 C. 0 D. 【答案】D 【解析】 - 22 - 【分析】 根据向量垂直,可得,由向量的模长计算公式,即可求得. 【详解】∵,,, 故可得 因此, 故选:D. 【点睛】本题考查向量模长的求解,以及向量垂直的坐标转化,属综合基础题. 6.程序框图所示的算法来自于《九章算术》.若输入的值为8,的值为6,则执行该程序框图输出的结果为( ) A. 1 B. 2 C. 3 D. 4 【答案】B 【解析】 【分析】 模拟执行程序框图,即可容易求得输出结果. 【详解】模拟执行程序框图,如下所示: - 22 - ,不满足,满足, ,不满足,不满足, ,不满足,不满足, ,满足,输出 故选:B. 【点睛】本题考查由程序框图计算输出结果,属基础题. 7.已知一个几何体的正视图和侧视图,其俯视图用斜二测画法所画出的水平放置的直观图是一个直角边长为1的等腰直角三角形(如图所示).则此几何体的表面积为( ) A. B. C. D. 4 【答案】C 【解析】 【分析】 根据斜二侧画法可知可知俯视图的形状,结合正视图和侧视图还原几何体,即可容易求得其表面积. 【详解】∵根据斜二侧画法可知,几何体的底面积是一个直角三角形,两直角边分别为2、, 且该几何体一个直三棱锥,如下所示: - 22 - 容易知,,, 故可得中上的高, 故可得, 且,,, 故该几何体的表面积为. 故选:. 【点睛】本题考查由三视图还原几何体,以及斜二侧画法的理解和辨析,属综合基础题. 8.在如图所示的阴阳鱼图案中,阴影部分可表示为或,若点,则的最大值是( ) A. B. 2 C. D. 【答案】C 【解析】 - 22 - 【分析】 求得直线与圆相切时的状态,数形结合,即为所求. 【详解】作直线,当直线上移与圆的右上方相切时,取最大值, 此时,利用圆心到直线的距离等于1, 解得的最大值为. 故选:C. 【点睛】本题考查线性目标函数的最值求解问题,涉及直线与圆相切,属综合基础题. 9.已知命题:函数f(x)的定义域为,命题:存在实数满足,若为真,则实数的取值范围是( ) A. B. C. D. 【答案】D 【解析】 【分析】 分别求得命题为真时对应参数的范围,根据复合命题为真,求得结果. 【详解】若命题为真,则在上恒成立, 故可得,解得; 若命题为真,则. 令,故可得,令,解得, 故容易得在单调递增,在上单调递减. 故.则. 所以若为真,则, 故选:D. - 22 - 【点睛】本题考查由复合命题的真假求参数范围,涉及利用导数求函数的最值,属综合基础题. 10.已知,分别是双曲线的左右焦点,过点与双曲线的一条渐近线平行的直线交双曲线的另一条渐近线于点,若,则该双曲线离心率的取值范围是( ) A. B. C. D. 【答案】D 【解析】 【分析】 求出点的坐标,根据向量数量积的正负,求得的关系式,结合离心率求解公式,即可容易求得. 【详解】不妨设过点与双曲线的一条渐进线平行的直线方程为, 与另一条渐近线的交点为, 由是, 即有,又因为, 故选:D. 【点睛】本题考查双曲线离心率范围的求解,属基础题. 11.已知是函数的最大值,若存在实数使得对任意实数总有成立,则的最小值为( ) A. B. C. D. 【答案】B 【解析】 【分析】 利用正弦的和角公式以及辅助角公式化简至标准型正弦函数,解得 - 22 - ,即可容易求得结果. 【详解】因为 ∴,周期, 又存在实数,对任意实数总有成立, ∴,, 的最小值为, 故选:B. 【点睛】本题考查利用三角恒等变换求函数解析式,正弦型三角函数的周期和最值,属综合基础题. 12.如图,矩形中,,为边的中点,将绕直线翻转成(平面),为线段的中点,则在翻折过程中,①与平面垂直的直线必与直线垂直;②线段的长恒为③异面直线与所成角的正切值为④当三棱锥的体积最大时,三棱锥外接球的体积是.上面说法正确的所有序号是( ) A. ①②④ B. ①③④ C. ②③ D. ①④ 【答案】A - 22 - 【解析】 【分析】 根据线面平行的判定定理,以及线面角的求解,棱锥外接球的求解,对选项进行逐一分析即可. 【详解】取的中点,的中点,连接,,,,显然//平面,故①正确; ,故②正确; 即为异面直线与所成角,,故③错误; 当三棱锥的体积最大时,则平面平面, 不妨取中点为,连接,则容易知平面, 因为,且,故可得, 又因为分别为中点,故可得, 故在中,. - 22 - 因为三棱锥的底面为直角三角形,且为斜边上的中点, 故可得,又, 故为三棱锥外接球球心,且,故④正确, 综上,①②④正确, 故选:A. 【点睛】本题考查线面平行的推证,线面夹角的求解,三棱锥外接球的求解,属综合中档题. 第Ⅱ卷 本卷包括必考题和选考题两个部分.第(13)题-第(21)题为必考题,每个考生都必须作答.第(22)题-第(23)题为选考题,考生根据要求作答. 二、填空题:本大题共4小题每小题5分,满分20分.把答案填在答题卡中对应题号后的横线上. 13.在区间上随机地取一个数,则事件“”发生的概率为__________. 【答案】 【解析】 【分析】 求得正弦不等式,根据几何概型的概率计算,即可容易求得. 【详解】∵在区间上,, 则, 因此其概率为. 故答案为:. 【点睛】本题考查三角不等式的求解,以及几何概型的概率求解,属综合基础题. 14.设抛物线的焦点为,过点作直线与抛物线分别交于两点、,若点满足,则__________. - 22 - 【答案】6 【解析】 【分析】 由焦点弦的弦长公式,结合向量关系,即可容易求得,则问题得解. 【详解】地物线的焦点,设,, ∵直线过焦点, ∴,又,则为中点, 所以. 故答案为:. 【点睛】本题考查抛物线焦点弦的求解,属基础题. 15.在中,内角、、所对的边分别为、、,若,则(1)__________,(2)的最大弧度数为___________. 【答案】 (1). 2 (2). 【解析】 【分析】 利用正余弦定理求得与的关系,利用均值不等式即可求得的最小值,则的最大值可解. 【详解】∵,∴; 又, ∵,∴, 当且仅当时取等号. 故答案为:;. - 22 - 【点睛】本题考查利用正弦定理实现角化边,以及用余弦定理解三角形,涉及均值不等式求和的最小值,属综合中档题. 16.己知直线上有两点、且满足若,则这样的点共有_____个. 【答案】2 【解析】 【分析】 根据已知条件,可得,结合弦长可得外接圆,由外接圆圆心的个数,可得结果. 【详解】由已知条件和数量积的定义可知或,又, 所以的外接圆的半径, 设其圆心为,则点到直线的距离为, 所以点应在与直线平行且距离为的两条平行直线、上, 且点到原点的距离为2; 而原点到的距离为,所以上不存在这样的点; 而原点到的距离为,所以上存在两个符合条件的点; 每个点都确定唯一一个点,所以这样的点共有2个. 故答案为:2. 【点睛】本题考查向量的数量积运算,正弦定理求外接圆半径,点到直线的距离公式,属综合中档题. 三、解答题:本大题必做题5个,每题12分,选做题两个只选做一个,10分,满分70分.解答应写出文字说明,证明过程或推演步骤. 17.已知的三个内角、、的对边分别为、、,且 - 22 - . (1)求角的大小; (2)若三边,,的长成等比数列,的面积为,求的长. 【答案】(1)(2), 【解析】 【分析】 (1)利用正弦定理将边化角,即可容易求得结果; (2)由正弦定理求得,结合余弦定理与已知条件,即可求得. 【详解】(1)∵ ∴ ∵,∴ (2)由的面积为得,又,∴ 由余弦定理知:∴ ∴ 所以. 【点睛】本题考查利用正余弦定理求解三角形,涉及正弦的和角公式,属综合基础题. 18.2020年1月22日,国新办发布消息:新型冠状病毒在武汉一家海鲜市场非法销售的野生动物上发现.专家通过全基因组比对发现此病毒与2003年的非典冠状病毒以及此后的中东呼吸综合征冠状病毒,分别达到70%和40%的序列相似性.这种新型冠状病毒对人们的健康生命带来了严重威胁因此,某生物疫苗研究所加紧对新型冠状病毒疫苗进行实验,并将某一型号疫苗用在动物小白鼠身上进行科研和临床实验,得到统计数据如下: 未感染病毒 感染病毒 总计 未注射疫苗 20 - 22 - 注射疫苗 30 总计 50 50 100 现从所有试验小白鼠中任取一只,取到“注射疫苗”小白鼠的概率为. (1)求列联表中的数据,,,的值; (2)能否有99.9%把握认为注射此种疫苗对预防新型冠状病毒有效? 附:. 0.05 0.01 0.005 0.001 3.841 6.635 7.879 10.828 【答案】(1),,,(2)有99.9%把握认为注射此种疫苗对预防新型冠状病毒有效 【解析】 【分析】 (1)根据题中简单事件的概率先求得,再结合表格中数据,即可求得其它数据; (2)根据表格,计算,再结合参考表格,进行判断. 【详解】(1)由已知条件可知:, ,,. (2)∵ 显然 所以有99.9%把握认为注射此种疫苗对预防新型冠状病毒有效. 【点睛】本题考查简单事件的概率计算,以及的计算,属基础题. 19.已知在四棱锥中,,,,, - 22 - 且平面平面 (1)设点为线段的中点,试证明平面; (2)若直线与平面所成的角为60°,求四棱锥的体积. 【答案】(1)证明见解析(2) 【解析】 分析】 (1)取中点为,通过面面垂直,结合//,即可容易证明; (2)根据线面角,求得,先证平面,结合即可容易求得. 【详解】(1)证明:取的中点,连接和, ∵在中,∴. 由于平面平面,且交线为,∴平面. 又∵,分别为,的中点,∴//且. 又//,,∴//且. - 22 - ∴四边形为平行四边形.∴//, ∴平面. (2)由(1)中所证,不妨取中点为,则一定有平面. 所以直线与平面所成的角为, 由于,∴, 又//∴、点到平面的距离相等, ∵平面平面,, ∴平面∴点到平面的距离等于2. 故可得; . 又因为点到平面的距离为,点到平面的距离为, ∴ 【点睛】本题考查面面垂直推证线面垂直,棱锥体积的求解,属综合基础题. 20.已知椭圆的离心率为,左右焦点分别为、,为椭圆上一点,与轴交于点,,. (1)求椭圆的方程; (2)设直线与椭圆相交于、两点,过作与轴垂直的直线,点坐标为,试问直线与直线交点的横坐标是否为定值,请说明理由. 【答案】(1)(2)横坐标为定值2,详见解析 【解析】 【分析】 (1)根据题意,列出的方程,即可容易求得椭圆方程; (2)设出直线方程与椭圆方程,结合韦达定理,求得直线方程,进而求得与直线交点的横坐标,即可容易证明. - 22 - 【详解】(1)连接,由题意得, 所以为中位线,又因为, 所以,且, 又,,得,, 故所求椭圆方程为. (2)设,由得 ∴ 直线的方程:, 令,则有 ∴与交点的横坐标为定值2. 【点睛】本题考查椭圆方程的求解,以及椭圆中定值问题的处理,属综合中档题. 21.若方程有实数根,则称为函数的一个不动点.已知函数(为自然对数的底数). (1)当时是否存在不动点?并证明你的结论; (2)若,求证有唯一不动点. 【答案】(1)不存在不动点;证明见解析(2)证明见解析 【解析】 【分析】 - 22 - (1)将问题转化为求方程的根,构造函数利用导数判断函数的单调性以及最小值,即可容易证明; (2)根据不动点的定义,结合(1)中的思路,即可容易求证. 【详解】(1)当时,不存在不动点. 证明:由可得:, 令,, 则, ∵,∴ 当时,,在上单调递减, 当时,,在上单调递增, 所以.所以方程无实数根 故不存在不动点. (2)当时,,, 则, 再令,∴ 当时,,在上单调递减, 当时,,在上单调递增, ∴ 故当时,,在上单调递减, 当时,,在上单调递增, - 22 - 所以 所以有唯一实数根, 故有唯一不动点. 【点睛】本题考查利用导数判断函数的单调性,以及最值的求解,属综合中档题. 请考生在(22).(23)两题中任选一题作答,注意:只能做所选定的题目如果多做,则按所做的第一个题目计分,作答时请用2B铅笔在答题卡上将所选题号后的方框涂黑 22.心形线是由一个圆上的一个定点,当该圆绕着与其相切且半径相同的另外一个圆周上滚动时,这个定点的轨迹,因其形状象心形而得名.在极坐标系中,方程表示的曲线就是一条心形线,如图,以极轴所在直线为轴,极点为坐标原点的直角坐标系中,已知曲线的参数方程为(为参数). (1)求曲线的极坐标方程; (2)若曲线与相交于、、三点,求线段的长. 【答案】(1)(2) 【解析】 【分析】 (1)先通过消参将其转化为普通方程,再利用公式求得其极坐标方程; (2)设出的极坐标系下的极坐标,即可容易求得结果. 【详解】(1)由,(为参数),消参数化简得普通方程:, 令,即 - 22 - 化简得,即 即得曲线的极坐标方程为. (2)由已知,不妨设,, 于是,, 故. 【点睛】本题考查极坐标方程和直角方程之间的转化,以及利用极坐标求弦长,属综合基础题. 23.已知函数的定义域为. (1)求实数的取值范围; (2)设为最大值,实数满足,试证明. 【答案】(1)(2)证明见解析 【解析】 【分析】 (1)根据定义域结合绝对值三角不等式,即可容易求得结果; (2)由(1)中所求,结合均值不等式即可容易求得结果. 【详解】(1)由题意知,恒成立, 又, 所以实数的取值范围是. (2)由(1)可知,,所以 从而, 当且仅当,即时等号成立,证毕. - 22 - 【点睛】本题考查利用绝对值不等式求最值,以及利用均值不等式求最值,属综合基础题. - 22 - - 22 -查看更多