2020高中数学 第三章 函数的应用 阶段复习课 第4课 函数的应用章末综合测评5 新人教A版必修1
章末综合测评(三) 函数的应用
(时间:120分钟 满分:150分)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知函数f(x)=则该函数的零点的个数为( )
【导学号:37102408】
A.1 B.2
C.3 D.4
C [当x<0时,令x(x+4)=0,解得x=-4;当x≥0时,令x(x-4)=0,解得x=0或4.综上,该函数的零点有3个.]
2.函数f(x)=ln(x+1)-的零点所在的大致区间是( )
A.(1,2) B.(0,1)
C.(2,e) D.(3,4)
A [f(1)=ln 2-2=ln
ln 1=0,
所以函数f(x)=ln(x+1)-的零点所在的大致区间是(1,2).]
3.以下每个图象表示的函数都有零点,但不能用二分法求函数零点的是( )
【导学号:37102409】
A B C D
C [二分法求函数零点时,其零点左右两侧的函数值符号相反,故选C.]
4.用二分法求函数f(x)=2x-3的零点时,初始区间可选为( )
A.[-1,0] B.[0,1]
C.[1,2] D.[2,3]
C [∵f(1)=2-3=-1<0,f(2)=4-3=1>0,
∴f(1)·f(2)<0,∴初始区间可选为[1,2].]
5.用二分法判断方程2x3+3x-3=0在区间(0,1)内的根(精确度0.25)可以是(参考数据:0.753=0.421 875,0.6253=0.244 14)( )
【导学号:37102410】
A.0.25 B.0.375
C.0.635 D.0.825
C [令f(x)=2x3+3x-3,f(0)<0,f(1)>0,f(0.5)<0,f(0.75)>0,f(0.625)<0.
∴方程2x3+3x-3=0的根在区间(0.625,0.75)内,
- 7 -
∵0.75-0.625=0.125<0.25,
∴区间(0.625,0.75)内的任意一个值作为方程的近似根都满足题意.]
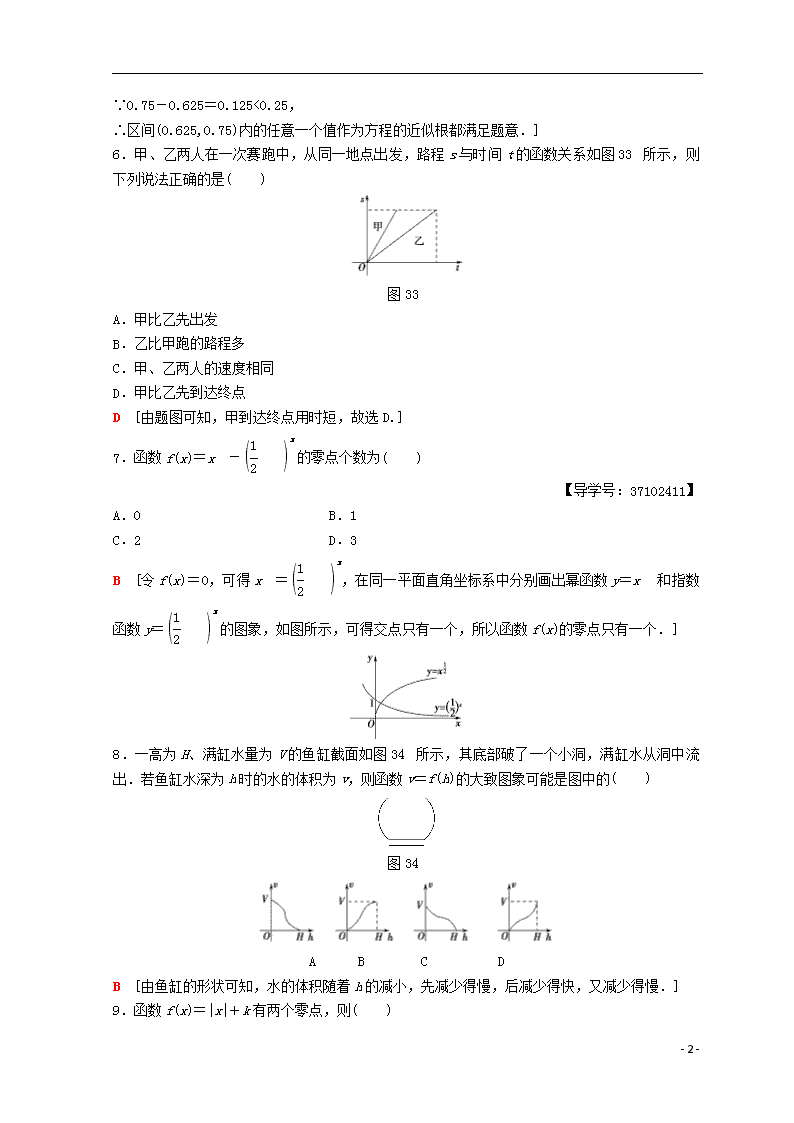
6.甲、乙两人在一次赛跑中,从同一地点出发,路程s与时间t的函数关系如图33所示,则下列说法正确的是( )
图33
A.甲比乙先出发
B.乙比甲跑的路程多
C.甲、乙两人的速度相同
D.甲比乙先到达终点
D [由题图可知,甲到达终点用时短,故选D.]
7.函数f(x)=x-x的零点个数为( )
【导学号:37102411】
A.0 B.1
C.2 D.3
B [令f(x)=0,可得x=x,在同一平面直角坐标系中分别画出幂函数y=x和指数函数y=x的图象,如图所示,可得交点只有一个,所以函数f(x)的零点只有一个.]
8.一高为H、满缸水量为V的鱼缸截面如图34所示,其底部破了一个小洞,满缸水从洞中流出.若鱼缸水深为h时的水的体积为v,则函数v=f(h)的大致图象可能是图中的( )
图34
A B C D
B [由鱼缸的形状可知,水的体积随着h的减小,先减少得慢,后减少得快,又减少得慢.]
9.函数f(x)=|x|+k有两个零点,则( )
- 7 -
【导学号:37102412】
A.k=0 B.k>0
C.0≤k<1 D.k<0
D [在同一平面直角坐标系中画出y1=|x|和y2=-k的图象,如图所示.若f(x)有两个零点,则必有-k>0,即k<0.
]
10.已知f(x)=(x-a)(x-b)-2,并且α,β是函数f(x)的两个零点,则实数a,b,α,β的大小关系可能是( )
A.a<α0,而00.]
12.设函数f(x)=若f(-4)=f(0),f(-2)=-2,则关于x的方程f(x)=x的解的个数是( )
A.1 B.2
C.3 D.4
C [因为f(-4)=f(0),f(-2)=-2,
所以解得
所以f(x)=
当x>0时,方程为x=2,此时方程f(x)=x只有1个解;
当x≤0时,方程为x2+4x+2=x,解得x=-1或x=-2,此时方程f(x)=x有2个解.所以方程f(x)=x共有3个解.]
二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)
- 7 -
13.如果函数f(x)=x2+mx+m+3的一个零点为0,则另一个零点是________.
【导学号:37102414】
3 [函数f(x)=x2+mx+m+3的一个零点为0,则f(0)=0,∴m+3=0,∴m=-3,则f(x)=x2-3x,于是另一个零点是3.]
14.用二分法求方程ln x-2+x=0在区间[1,2]上零点的近似值,先取区间中点c=,则下一个含根的区间是________.
[令f(x)=ln x-2+x,则f(1)=ln 1-2+1<0,
f(2)=ln 2-2+2=ln 2>0,
f=ln -2+=ln -=ln -ln =ln =ln 1时,判断函数f(x)在区间(0,m)内是否存在零点.
【导学号:37102416】
[解] f(x)=ex-m-x,所以f(0)=e-m-0=e-m>0,
f(m)=e0-m=1-m.
又m>1,所以f(m)<0,
所以f(0)·f(m)<0.
又函数f(x)的图象在区间[0,m]上是一条连续曲线,
故函数f(x)=ex-m-x(m>1)在区间(0,m)内存在零点.
- 7 -
18.(本小题满分12分)为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=(0≤x≤10),若不建隔热层,每年能源消费费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.求k的值及f(x)的解析式.
[解] 设隔热层厚度为x cm,
由题设,每年能源消耗费用为C(x)=(0≤x≤10),
再由C(0)=8,得k=40,因此C(x)=.
而建造费用为C1(x)=6x.
最后得隔热层建造费用与20年的能源消耗费用之和为f(x)=20C(x)+C1(x)=20×+6x=+6x(0≤x≤10).
19.(本小题满分12分)如图35,直角梯形OABC位于直线x=t右侧的图形的面积为f(t).
图35
(1)试求函数f(t)的解析式;
(2)画出函数y=f(t)的图象.
【导学号:37102417】
[解] (1)当0≤t≤2时,
f(t)=S梯形OABC-S△ODE=-t·t=8-t2,
当20),
∴f(x)在区间[-1,4]上的最大值是f(-1)=6a.
由已知,得6a=12,
∴a=2.
∴f(x)=2x(x-5)=2x2-10x(x∈R).
(2)由(1)知f(x)=2x2-10x=22-,开口向上,对称轴为x=.
- 7 -
①当t+1<,即t<时,f(x)在[t,t+1]上是减函数,∴g(t)=2(t+1)2-10(t+1)=2t2-6t-8.
②当t>时,f(x)在[t,t+1]上是增函数,
∴g(t)=2t2-10t.
③当t≤≤t+1,即≤t≤时,f(x)在对称轴处取得最小值,∴g(t)=f=-.
综上所述,g(t)=
22.(本小题满分12分)芦荟是一种经济价值很高的观赏、食用植物,不仅可美化居室、净化空气,又可美容保健,因此深受人们欢迎,在国内占有很大的市场.某人准备进军芦荟市场,栽培芦荟,为了了解行情,进行市场调研,从4月1日起,芦荟的种植成本Q(单位:元/10 kg)与上市时间t(单位:天)的数据情况如下表:
t
50
110
250
Q
150
108
150
(1)根据上表数据,从下列函数中选取一个最能反映芦荟种植成本Q与上市时间t的变化关系:Q=at+b,Q=at2+bt+c,Q=a·bt,Q=alogbt;
(2)利用你选择的函数,求芦荟种植成本最低时的上市天数及最低种植成本.
[解] (1)由所提供的数据可知,刻画芦荟种植成本Q与上市时间t的变化关系的函数不可能是常值函数,若用函数Q=at+b,Q=a·bt,Q=alogbt中的任意一个来反映时都应有a≠0,且上述三个函数均为单调函数,这与表格所提供的数据不符合,所以应选用二次函数Q=at2+bt+c进行描述,将表格所提供的三组数据分别代入函数Q=at2+bt+c,可得:
解得a=,b=-,c=.
所以,刻画芦荟种植成本Q与上市时间t的变化关系的函数为Q=t2-t+.
(2)当t=-=150(天)时,芦荟种植成本最低为Q=×1502-×150+=100(元/10 kg).
- 7 -