2020学年高二数学下学期期末考试试题 理(新版)新人教版

2020学年高二数学下学期期末考试试题 理(新版)新人教版

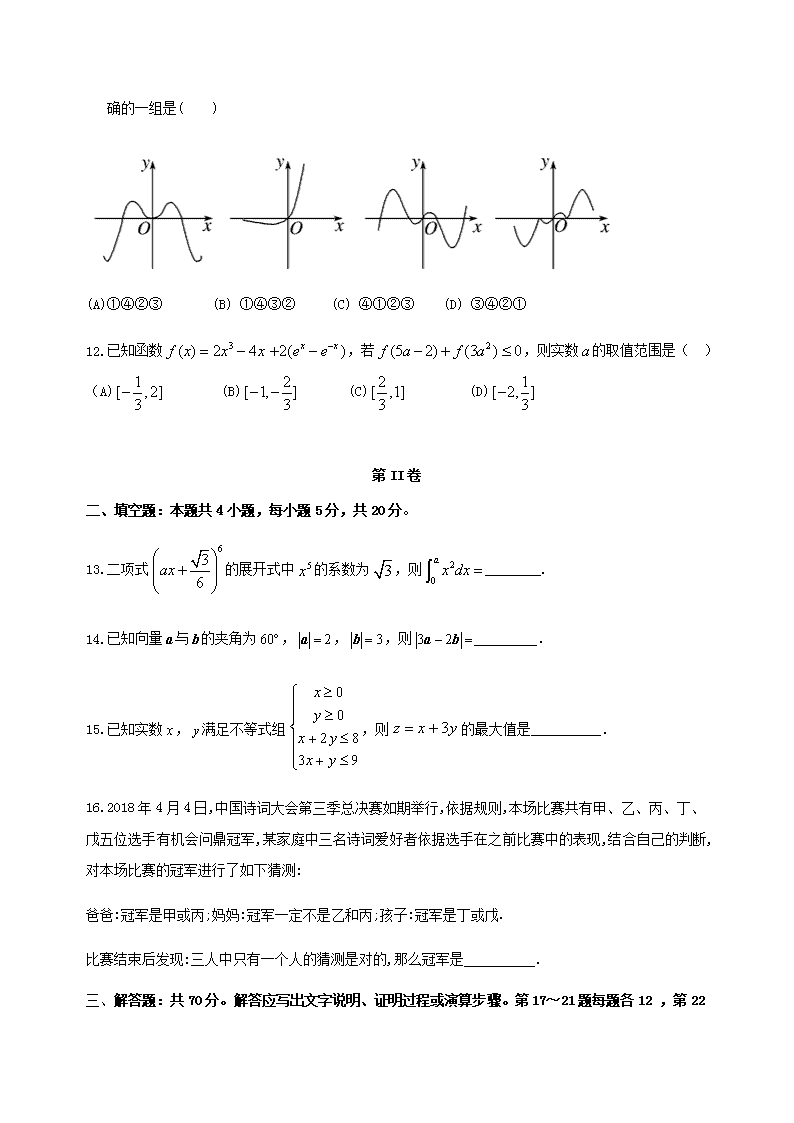
‎2019学年度第二学期期末考试 ‎ 高二年级 数学（理科）试卷 考生注意:‎ ‎1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分.考试时间120分钟.‎ ‎2．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。‎ ‎3．作答时，请将各题答案填在答题卡上。写在本试卷及草稿纸上无效。‎ 第I卷 一、选择题：本题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎1． 若（为虚数单位），则复数（ ）‎ ‎(A) (B) (C) (D) ‎ ‎2．设集合， ， ，则中的元素个数为（ ）‎ ‎(A) (B) (C) (D) ‎ ‎3.如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体各面中直角三角形的个数是( ) （A）2 （B）3 （C）4 （D）5‎ ‎4.为第三象限角，，则（ ）‎ ‎(A) (B) (C) (D)‎ ‎5.第十九届西北医疗器械展览将于2018年5月18至20日在兰州举行,现将5‎ 名志愿者分配到3个不同的展馆参加接待工作，每个展馆至少分配一名志愿者的分配方案种数为（ ）‎ ‎(A) 540 (B) 300 (C) 180 (D) 150‎ ‎6．执行如图所示的程序框图，若输出的，则判断框内应填入的条件是（ ）‎ ‎(A) (B) (C) (D)‎ ‎7.已知双曲线的焦距是虚轴长的倍，则该双曲线的渐近线方程为（ ）‎ ‎(A) (B) (C) (D) ‎ ‎8.下列有关统计知识的四个命题正确的是（ ）‎ ‎(A)衡量两变量之间线性相关关系的相关系数越接近，说明两变量间线性关系越密切。 ‎ ‎(B)在回归分析中，可以用卡方来刻画回归的效果，越大，模型的拟合效果越差。 ‎ ‎(C)线性回归方程对应的直线至少经过其样本数据点中的一个点。 ‎ ‎(D)线性回归方程中，变量每增加一个单位时，变量平均增加个单位。‎ ‎9.某班级有男生人，女生人，现选举名学生分别担任班长、副班长、团支部书记和体育班委.男生当选的人数记为，则的数学期望为（ ）‎ ‎(A) (B) (C) (D)‎ ‎10.已知三棱锥的所有顶点都在球的球面上，，，若三棱锥体积的最大值为2，则球的表面积为( )‎ ‎（A） （B） （C） （D） ‎ ‎11.给出下列四个函数：①；②；③；④.‎ 这四个函数的部分图象如下，但顺序被打乱，则按照从左到右的顺序将图象对应的函数序号安排正确的一组是(　　)‎ ‎(A)①④②③ (B) ①④③② (C) ④①②③ (D) ③④②①‎ ‎12.已知函数，若，则实数的取值范围是（ ）（A) (B) (C) (D)‎ 第II卷 二、填空题：本题共4小题，每小题5分，共20分。‎ ‎13.二项式的展开式中的系数为，则________.‎ ‎14.已知向量与的夹角为，，，则_________．‎ ‎15.已知实数，满足不等式组，则的最大值是__________．‎ ‎16.2018年4月4日,中国诗词大会第三季总决赛如期举行,依据规则,本场比赛共有甲、乙、丙、丁、戊五位选手有机会问鼎冠军,某家庭中三名诗词爱好者依据选手在之前比赛中的表现,结合自己的判断,对本场比赛的冠军进行了如下猜测:‎ 爸爸:冠军是甲或丙;妈妈:冠军一定不是乙和丙;孩子:冠军是丁或戊.‎ 比赛结束后发现:三人中只有一个人的猜测是对的,那么冠军是 ．‎ 三、 解答题：共70分。解答应写出文字说明、证明过程或演算步骤。第17～21题每题各12 ，第22题 ‎10分。‎ ‎17.（本小题满分12分）已知等差数列{an}满足：a3＝7，a5＋a7＝26，{an}的前n项和为Sn.‎ ‎(1)求an及Sn；‎ ‎(2)令bn＝(n∈N*)，求数列{bn}的前n项和Tn.‎ ‎18.（本小题满分12分） 深受广大球迷喜爱的某支欧洲足球队.在对球员的使用上总是进行数据分析，为了考察甲球员对球队的贡献，现作如下数据统计：‎ 球队胜 球队负 总计 甲参加 甲未参加 总计 ‎（1）求的值，据此能否有的把握认为球队胜利与甲球员参赛有关；‎ ‎（2）根据以往的数据统计，乙球员能够胜任前锋、中锋、后卫以及守门员四个位置，且出场率分别为：，当出任前锋、中锋、后卫以及守门员时，球队输球的概率依次为：0.4,0.2,0.6,0.2.则：‎ 当他参加比赛时，求球队某场比赛输球的概率；‎ ‚当他参加比赛时，在球队输了某场比赛的条件下，求乙球员担当前锋的概率；‎ 附表及公式：‎ ‎.‎ ‎19．（12分）如图，在中，，是的中点，‎ 是线段上的一点，且，，将沿折起使得二面角是直二面角．‎ ‎（l）求证：平面；‎ ‎（2）求直线与平面所成角的正切值．‎ ‎20.（本小题满分12分）如图，椭圆经过点，且点到椭圆的两焦点的距离之和为．‎ ‎（l）求椭圆的标准方程；‎ ‎（2）若，是椭圆上的两个点，线段的中垂线的斜率为且直线与交于点，为坐标原点，求证：，，三点共线． ‎ ‎21.（本小题满分12分）已知函数，.‎ ‎（1）若曲线在处的切线与直线垂直，求实数的值；‎ ‎（2）设，若对任意两个不等的正数，都有恒成立，求实数的取值范围；‎ ‎22.（本小题满分10分）在△ABC中，角A，B，C所对的边分别为a，b，c，且．‎ ‎（1）判断△ABC的形状；‎ ‎（2）若，求的取值范围．‎ ‎2017_2018学年度第二学期期末 高二理科 数学 参考答案 第I卷 一、选择题：本题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎1． 若（为虚数单位），则复数（ B ）‎ ‎(A) (B) (C) (D) ‎ ‎2．设集合， ， ，则中的元素个数为（ C ）‎ ‎(A) (B) (C) (D) ‎ ‎3.如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体各面中直角三角形的个数是( C ) （A）2 （B）3 （C）4 （D）5‎ ‎4.为第三象限角，，则（ B ）‎ ‎(A) (B) (C) (D)‎ ‎5.第十九届西北医疗器械展览将于2018年5月18至20日在兰州举行,现将5名志愿者分配到3个不同的展馆参加接待工作，每个展馆至少分配一名志愿者的分配方案种数为 （ D ）‎ ‎(A) 540 (B) 300 (C) 180 (D) 150‎ ‎6．执行如图所示的程序框图，若输出的，则判断框内应填入的条件是（ A ）‎ ‎(A) (B) ‎ ‎(C) (D)‎ ‎7.已知双曲线的焦距是虚轴长的倍，则该双曲线的渐近线方程为（ A ）‎ ‎(A) (B) ‎ ‎(C) (D) ‎ ‎8.下列有关统计知识的四个命题正确的是（ A ）‎ ‎(A)衡量两变量之间线性相关关系的相关系数越接近，说明两变量间线性关系越密切。 ‎ ‎(B)在回归分析中，可以用卡方来刻画回归的效果，越大，模型的拟合效果越差。 ‎ ‎(C)线性回归方程对应的直线至少经过其样本数据点中的一个点。 ‎ ‎(D)线性回归方程中，变量每增加一个单位时，变量平均增加个单位。‎ ‎9.某班级有男生人，女生人，现选举名学生分别担任班长、副班长、团支部书记和体育班委.男生当选的人数记为，则的数学期望为（C ）‎ ‎(A) (B) (C) (D) ‎ ‎10.已知三棱锥的所有顶点都在球的球面上，，，若三棱锥体积的最大值为2，则球的表面积为( D )‎ ‎（A） （B） （C） （D） ‎ ‎11.给出下列四个函数：①；②；③；④.‎ 这四个函数的部分图象如下，但顺序被打乱，则按照从左到右的顺序将图象对应的函数序号安排正确的一组是(　A　)‎ ‎(A)①④②③ (B) ①④③② (C) ④①②③ (D) ③④②①‎ ‎12.已知函数，若，则实数的取值范围是（ D ）‎ ‎（A) (B) (C) (D)‎ 第II卷 二、填空题：本题共4小题，每小题5分，共20分。‎ ‎13.二项式的展开式中的系数为，则________.‎ ‎14.已知向量与的夹角为，，，则____6______．‎ ‎15.已知实数，满足不等式组，则的最大值是___12_______．‎ ‎16.2018年4月4日,中国诗词大会第三季总决赛如期举行,依据规则,本场比赛共有甲、乙、丙、丁、戊五位选手有机会问鼎冠军,某家庭中三名诗词爱好者依据选手在之前比赛中的表现,结合自己的判断,对本场比赛的冠军进行了如下猜测:‎ 爸爸:冠军是甲或丙;妈妈:冠军一定不是乙和丙;孩子:冠军是丁或戊.‎ 比赛结束后发现:三人中只有一个人的猜测是对的,那么冠军是 丙 ．‎ 三、 解答题：共70分。解答应写出文字说明、证明过程或演算步骤。第17～21题每题各12 ，第22题10分。‎ ‎17.（本小题满分12分）已知等差数列{an}满足：a3＝7，a5＋a7＝26，{an}的前n项和为Sn.‎ ‎(1)求an及Sn；‎ ‎(2)令bn＝(n∈N*)，求数列{bn}的前n项和Tn.‎ 解　(1)设等差数列{an}的首项为a1，公差为d.‎ 因为a3＝7，a5＋a7＝26，所以 解得所以an＝3＋2(n－1)＝2n＋1，Sn＝3n＋×2＝n2＋2n.‎ 所以，an＝2n＋1，Sn＝n2＋2n..........(6分）‎ ‎(2)由(1)知an＝2n＋1，‎ 所以bn＝＝＝＝，‎ 所以Tn＝(1－＋－＋…＋－)＝(1－)＝‎ 即数列{bn}的前n项和Tn＝ ...........(12分）‎ ‎18.（本小题满分12分） 深受广大球迷喜爱的某支欧洲足球队.在对球员的使用上总是进行数据分析，为了考察甲球员对球队的贡献，现作如下数据统计：‎ 球队胜 球队负 总计 甲参加 甲未参加 总计 ‎（1）求的值，据此能否有的把握认为球队胜利与甲球员参赛有关；‎ ‎（2）根据以往的数据统计，乙球员能够胜任前锋、中锋、后卫以及守门员四个位置，且出场率分别为：，当出任前锋、中锋、后卫以及守门员时，球队输球的概率依次为：‎ ‎0.4,0.2,0.6,0.2.则：‎ 当他参加比赛时，求球队某场比赛输球的概率；‎ ‚当他参加比赛时，在球队输了某场比赛的条件下，求乙球员担当前锋的概率；‎ 附表及公式：‎ ‎.‎ 解：（1）,‎ 有的把握认为球队胜利与甲球员参赛有关...........（6分）‎ ‎（2）设表示“乙球员担当前锋”；表示“乙球员担当中锋 ”；表示“乙球员担当后卫”；表示“乙球员担当守门员”；表示“球队输掉某场比赛”，则 ‎.‎ ‚................(12分）‎ ‎19．（12分）如图，在中，，是的中点，是线段上的一点，且，，将沿折起使得二面角是直二面角．‎ ‎（l）求证：平面；‎ ‎（2）求直线与平面所成角的正切值．‎ 解:（1）因为，所以，又，，‎ 所以，又因为，‎ 所以是的斜边上的中线，‎ 所以是的中点，又因为是的中点。所以是的中位线，所以，‎ 又因为平面，平面，所以平面．........(5分）‎ ‎（2）据题设分析知，，，两两互相垂直，以为原点，，，分别为，，轴建立如图所示的空间直角坐标系：‎ 因为，且，分别是，的中点，‎ 所以，，‎ 所以，，，，‎ 所以，，，‎ 设平面的一个法向量为，‎ 则，即，所以，令，则，‎ 设直线与平面所成角的大小为，则．‎ 故直线与平面所成角的正切值为．..............(12分）‎ ‎20.（本小题满分12分）如图，椭圆经过点，且点到椭圆的两焦点的距离之和为．‎ ‎（l）求椭圆的标准方程；‎ ‎（2）若，是椭圆上的两个点，线段的中垂线的斜率为且直线与交于点，为坐标原点，求证：，，三点共线． ‎ 解：（1）因为点到椭圆的两焦点的距离之和为，‎ 所以，解得．‎ 又椭圆经过点，所以．‎ 所以．所以椭圆的标准方程为．...........（4分）‎ ‎（2）因为线段的中垂线的斜率为，‎ 所以直线的斜率为．所以可设直线的方程为．‎ 据得，设点，，，‎ 所以，，‎ 所以，，‎ 因为，所以，所以点在直线上，‎ 又点，也在直线上，‎ 所以，，三点共线．..............(12分）‎ ‎21.（本小题满分12分）已知函数，.‎ ‎（1）若曲线在处的切线与直线垂直，求实数的值；‎ ‎（2）设，若对任意两个不等的正数，都有恒成立，求实数的取值范围；‎ 解：（1）由，得.　　‎ 由题意，，所以.　　　　　　　　　　　…………（4分）‎ ‎（2）.‎ 因为对任意两个不等的正数，都有恒成立，设，则即恒成立. ‎ 问题等价于函数，‎ 即在上为增函数，　　　　　‎ 所以在上恒成立.即在上恒成立.‎ 所以，即实数的取值范围是.　　　…………（12分）‎ ‎22.（本小题满分10分）在△ABC中，角A，B，C所对的边分别为a，b，c，且 ‎．‎ ‎（Ⅰ）判断△ABC的形状；‎ ‎（Ⅱ）若，求的取值范围．‎ 解答：（Ⅰ）因为，‎ 由正弦定理可得．‎ 即，所以．‎ 因为在△ABC中，，所以又，‎ 所以，．所以△ABC为的直角三角形．...............(5分）‎ ‎（Ⅱ）因为=．‎ 所以．因为△ABC是的直角三角形，‎ 所以，且，所以当时，有最小值是．‎ 所以的取值范围是．................（10分）‎