- 2021-06-23 发布 |
- 37.5 KB |
- 8页

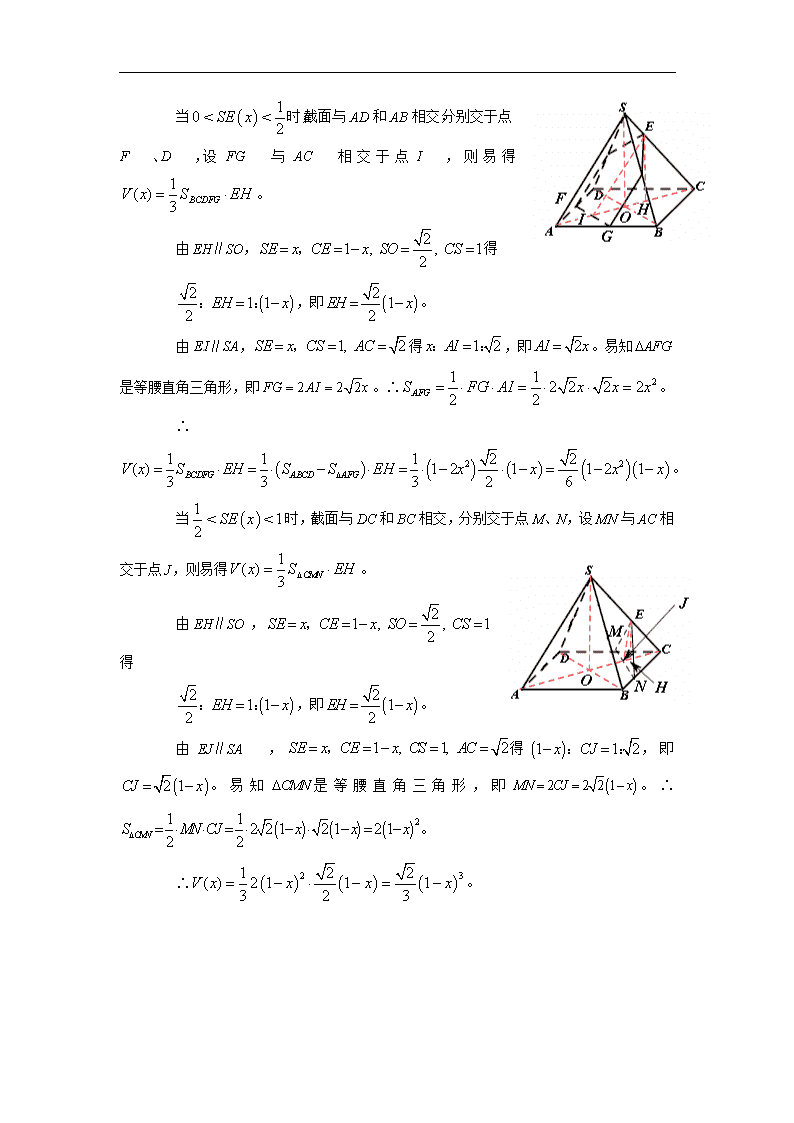
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
备战2014高考数学 高频考点归类分析(真题为例):多面体及球体的概念、性质、计算
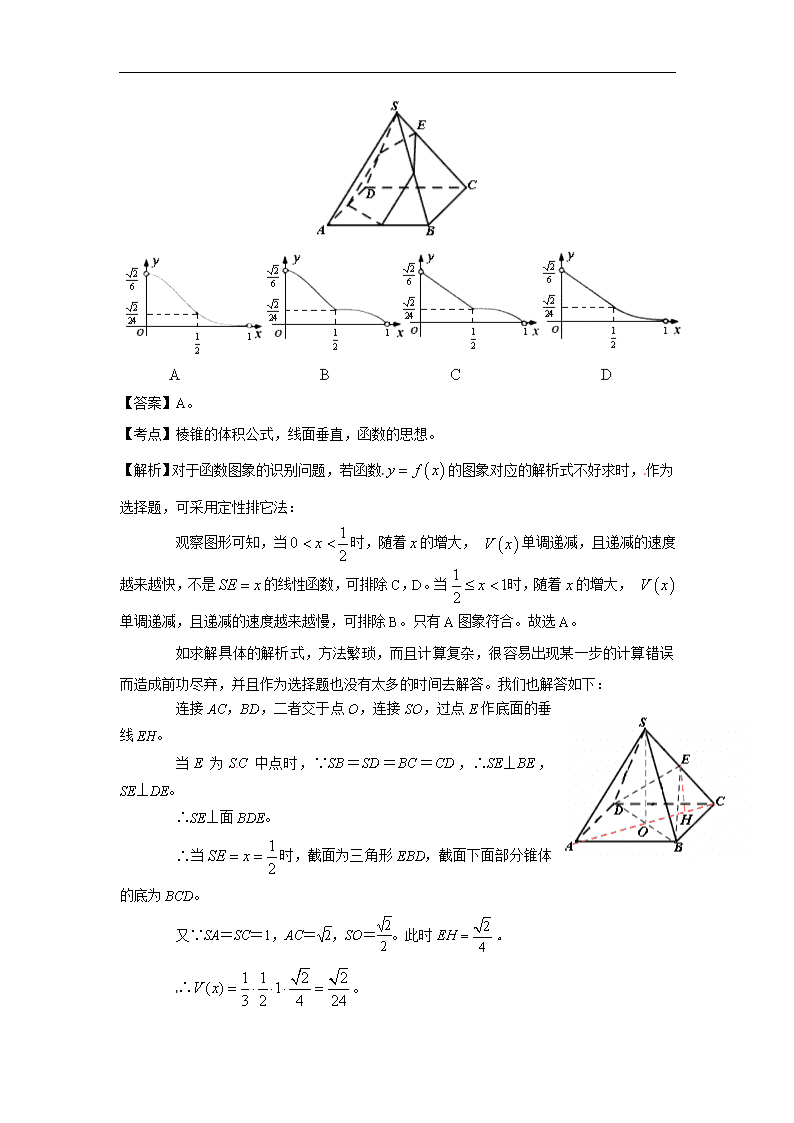
多面体及球体的概念、性质、计算 典型例题: 例1. (2012年全国课标卷理5分)已知三棱锥的所有顶点都在球的球面上,是边长为的正三角形,为球的直径,且;则此棱锥的体积为【 】 [来源:学科网] 【答案】。 【考点】三棱锥的性质。 【解析】∵的外接圆的半径,∴点到面的距离。 又∵为球的直径,∴点到面的距离为。 ∴ 此棱锥的体积为。故选。 例2. (2012年全国课标卷文5分)平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为,则此球的体积为 【 】 (A)π (B)4π (C)4π (D)6π 【答案】B。 【考点】点到平面的距离,勾股定理,球的体积公式。 【解析】由勾股定理可得球的半径为,从而根据球的体积公式可求得该球的体积为: 。故选B。 例3. (2012年江西省理5分)如下图,已知正四棱锥所有棱长都为1,点是侧棱上一动点,过点垂直于的截面将正四棱锥分成上、下两部分,记截面下面部分的体积为则函数的图像大致为【 】 【答案】A。[来源:学科网ZXXK] 【考点】棱锥的体积公式,线面垂直,函数的思想。 【解析】对于函数图象的识别问题,若函数的图象对应的解析式不好求时,作为选择题,可采用定性排它法: 观察图形可知,当时,随着的增大, 单调递减,且递减的速度越来越快,不是的线性函数,可排除C,D。当时,随着的增大, 单调递减,且递减的速度越来越慢,可排除B。只有A图象符合。故选A。 如求解具体的解析式,方法繁琐,而且计算复杂,很容易出现某一步的计算错误而造成前功尽弃,并且作为选择题也没有太多的时间去解答。我们也解答如下: 连接AC,BD,二者交于点O,连接SO,过点E作底面的垂线EH。 当E为SC中点时,∵SB=SD=BC=CD,∴SE⊥BE,SE⊥DE。 ∴SE⊥面BDE。 ∴当时,截面为三角形EBD,截面下面部分锥体的底为BCD。 又∵SA=SC=1,AC=,SO=。此时。 ∴。 当时,截面与AD和AB相交,分别交于点F、D,设FG与AC相交于点I,则易得。 由EH∥SO,得 ,即。 由EI∥SA,得,即。易知是等腰直角三角形,即。∴。 ∴。 当时,截面与DC和BC相交,分别交于点M、N,设MN与AC相交于点J,则易得。 由EH∥SO,得[来源:学#科#网] ,即。 由EJ∥SA,得,即。易知是等腰直角三角形,即。∴。 ∴。 综上所述,。 结合微积分知识,可判定A正确。 例4. (2012年湖北省理5分)我国古代数学名著《九章算术》中“开立圆术”曰:置积尺数,以十六乘之,九而一,所得开立方除之,即立圆径,“开立圆术”相当于给出了已知球的体积V,求其直径d的一个近似公式。人们还用过一些类似的近似公式。根据=3.14159…..判断,下列近似公式中最精确的一个是【 】 A. B. C. D. 【答案】D。 【考点】球的体积公式以及估算。 【解析】由球的体积公式得,由此得。对选项逐一验证: 对于A. 有,即; 对于B. 有,即; 对于C. 有,即; 对于D. 有,即; ∴中的数值最接近。故选D。 例5. (2012年重庆市理5分)设四面体的六条棱的长分别为1,1,1,1,和,且长为的棱与长为的棱异面,则的取值范围是【 】 (A) (B) (C) (D) 【答案】A。 【考点】异面直线的判定,棱锥的结构特征,勾股定理和余弦定理的应用。 【分析】如图所示,设四面体的棱长为,取中点P,连接,所以,在中,由勾股定理得=。 ∴在中, 。 ∵,∴。∴ ∴。故选A。 例6. (2012年上海市理4分)若一个圆锥的侧面展开图是面积为的半圆面,则该圆锥的体积为 ▲ . 【答案】。[来源:Zxxk.Com] 【考点】空间几何体的体积公式和侧面展开图。 【解析】根据该圆锥的底面圆的半径为,母线长为,根据条件得到,解得母线长,所以该圆锥的体积为:。 例7. (2012年上海市文4分)一个高为2的圆柱,底面周长为,该圆柱的表面积为 ▲ 【答案】。 【考点】圆柱的表面积。 【解析】根据该圆柱的底面周长得底面圆的半径为,所以该圆柱的表面积为: 。 例9. (2012年上海市理4分)如图,与是四面体中互相垂直的棱, ,若, 且,其中、为常数,则四面体的体积的最大值是 ▲ . 【答案】。 【考点】四面体中线面的关系,椭圆的性质。 【解析】作于,连接,则 ∵,,∴⊥平面。 又∵平面,∴。 由题设,,∴与都在以为焦距的椭球上,且、都垂直于焦距所在直线。∴=。 取中点,连接, ∵,∴⊥,,。 ∴。 ∴四面体的体积。[来源:Z#xx#k.Com] 显然,当在中点,即是短轴端点时,有最大值为。 ∴。 例10. (2012年山东省理4分)如图,正方体ABCD-A1B1C1D1的棱长为1。E,F分别为线段AA1,B1C上的点,则三棱锥D1-EDF的体积为 ▲ 。 【答案】 【考点】三棱锥的面积。 【解析】∵三棱锥与三棱锥表示的是同一棱锥,∴。 又∵的底△DD1E的面积是正方形面积的一半,等于;底△DD1E上的高等于正方形的棱长1, ∴。 例11. (2012年安徽省文5分)若四面体的三组对棱分别相等,即,, ,则 ▲ _.(写出所有正确结论编号) ①四面体每组对棱相互垂直 ②四面体每个面的面积相等 ③从四面体每个顶点出发的三条棱两两夹角之和大于而小于 ④连接四面体每组对棱中点的线段互垂直平分 ⑤从四面体每个顶点出发的三条棱的长可作为一个三角形的三边长 【答案】②④⑤。 【考点】四面体的性质。 【解析】①四面体每组对棱不相互垂直,命题错误; ②四面体每个面是全等三角形,面积相等,命题正确;[来源:Z|xx|k.Com] ③从四面体每个顶点出发的三条棱两两夹角之和等于,命题错误; ④连接四面体每组对棱中点构成菱形,线段互垂直平分,命题正确; 例12. (2012年辽宁省文5分)已知点是球O表面上的点,PA⊥平面ABCD,四边形ABCD是边长为2正方形。若,则△OAB的面积为 ▲ . 【答案】。 【考点】组合体的的位置关系,转化思想的应用。 【解析】∵点是球O表面上的点,PA⊥平面ABCD, ∴点为球O内接长方体的顶点,球心O为长方体对角线的中点。 ∴△OAB的面积是该长方体对角面面积的。 ∵,∴。∴。 例13. (2012年江苏省5分)如图,在长方体中,,,则四棱锥的体积为 ▲ cm3. 【答案】6。 【考点】正方形的性质,棱锥的体积。 【解析】∵长方体底面是正方形,∴△中 cm,边上的高是cm(它也是中上的高)。 ∴四棱锥的体积为。查看更多