2017-2018学年河北省定州市高二上学期期中考试数学（理）试题 解析版

2017-2018学年河北省定州市高二上学期期中考试数学（理）试题 解析版

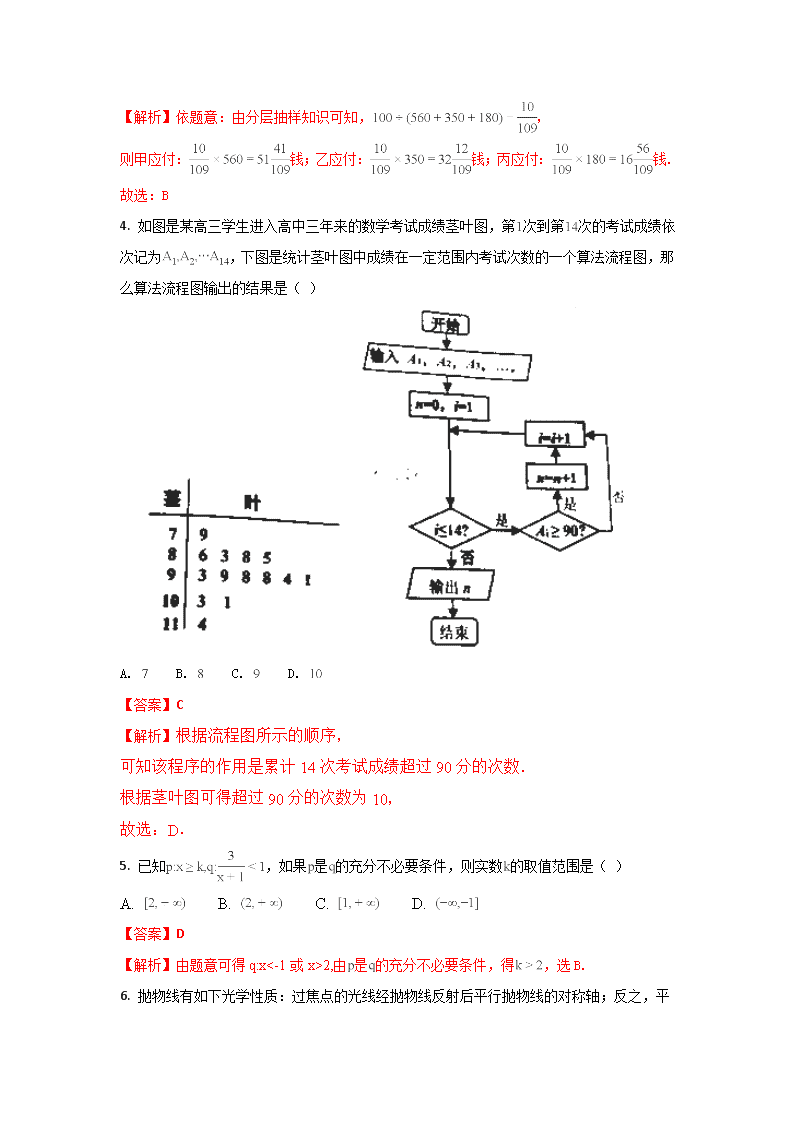
定州市 2017-2018 学年度第一学期期中考试 高二理科数学试卷 一、选择题：本大题共 12 个小题,每小题 5 分,共 60 分.在每小题给出的四个选 项中，只有一项是符合题目要求的. 1. 双曲线 的渐近线方程为（ ） A. B. C. D. 【答案】A 【解析】令 得： ，所以双曲线的渐进线方程 ，故选 A. 2. 以下判断正确的是（ ） A. 命题“若 ，则 ”为真命题 B. 命题“ ”的否定是 “ ” C. “ ”是“函数 是偶函数”的 充要条件 D. 命题“在 中，若 ，则 ”为假命题 【答案】C 【解析】A 选项中 正负不知所以不正确；B 选项中命题的否定是 ，所以 B 错误；C 选项中，当 时， ，所以是偶函数，故 C 正确，选 C. 3. 分层抽样是将总体分成互不交叉的层，然后按照一定的比例，从各层独立地抽取一定数 量的个体，组成一个样本的抽样方法；在《九章算术》第三章“衰分”中有如下问题：“今 有甲持钱五百六十，乙持钱三百五十，丙持钱一百八十，凡三人俱出关，关税百钱.欲以钱 多少衰出之，问各几何？”其译文为：今有甲持 钱，乙持 钱，丙持 钱，甲、乙、 丙三人一起出关，关税共 钱，要按照各人带多少的比例进行交税，问三人各应付多少税？ 则下列说法错误的是（ ） A. 甲应付 钱 B. 乙应付 钱 C. 丙应付 钱 D. 三者中甲付的钱最 多，丙付的钱最少 【答案】B 【解析】依题意：由分层抽样知识可知， ， 则甲应付： 钱；乙应付： 钱；丙应付： 钱. 故选：B 4. 如图是某高三学生进入高中三年来的数学考试成绩茎叶图，第 次到第 次的考试成绩依 次记为 ，下图是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图，那 么算法流程图输出的结果是（ ） A. B. C. D. 【答案】C 【解析】根据流程图所示的顺序， 可知该程序的作用是累计 14 次考试成绩超过 90 分的次数． 根据茎叶图可得超过 90 分的次数为 10， 故选：D． 5. 已知 ，如果 是 的充分不必要条件，则实数 的取值范围是（ ） A. B. C. D. 【答案】D 【解析】由题意可得 q:x<-1 或 x>2,由 是 的充分不必要条件，得 ，选 B. 6. 抛物线有如下光学性质：过焦点的光线经抛物线反射后平行抛物线的对称轴；反之，平 行于抛物线对称轴的入射光线经抛物线反射后必过抛物线的焦点.已知抛物线 的焦点 为 ，一条平行于 轴的光线从点 射出，经过抛物线上的点 反射后，再经抛物线上的 另一点 射出，则直线 的斜率为（ ） A. B. C. D. 【答案】A 【解析】令 y=1,代入 ，得 ，即 ,由抛物线的光学性质可知，直线 AB 经过 焦点 F(1,0),所以 直线 的斜率为 ，故选 A 7. 如图在 中，在线段 上任取一点 ，恰好满足 的概率是（ ） A. B. C. D. 【答案】C 8. 双曲线 的离心率为 ，则 的最小值是（ ） A. B. C. D. 【答案】A 【解析】依题意 ，故 . 9. 连掷一枚均匀的骰子两次，所得向上的点数分别为 ，记 ，则（ ） A. 事件“ ”的概率为 B. 事件“ ”的概率为 C. 事件“ ”与 “ ”互为对立事件 D. 事件“ 是奇数”与“ ”互为互斥事件 【答案】D 【解析】事件“ ” 的概率为 ， 错；“ ”的概率为 ， 错；事件“ ”与“ ” 可以同时发生， 错误；若 ，则 是偶数，事件“ 是奇数”与“ ”互为互斥事 件正确，D 正确，故选 D. 10. 把离心率 的双曲线 称之为黄金双曲线，若以原点为圆心， 以虚半轴长为半径画圆 ，则圆 与黄金双曲线（ ） A. 无交点 B. 有 个交点 C. 有 个交点 D. 有 个交点 【答案】D 11. 年年岁史诗大剧《芈月传》风靡大江南北，影响力不亚于以前的《甄嬛传》，某记 者调查了大量《芈月传》的观众，发现年龄段与爱看的比例存在较好的线性相关关系，年龄 在 的爱看比例分别为 ，现用这 个 年龄段的中间值 代表年龄段，如 代表 代表 ，根据前四个数据求得 关于爱 看比例 的线性回归方程为 ，由此可推测的值为（ ） A. B. C. D. 【答案】B 【解析】由题意可知：前四个数据的 ， 代入线性回归方程 ，得 ，当 时，代入线性回归方程 ，故选 B. 点睛：本题主要考查了线性回归方程及相关问题，属于中档题，线性回归直线方程按最小二 乘法计算时，必过这组数据的中心点 ，所以求回归直线方程中参数时，只需代入中心点 即可，线性回归方程的用途是用来预测估算的，因此预测时只需代入相应的 ，即可得到预 估值 . 12. 设 为椭圆 与双曲线 的公共的左右焦点，它们在第一象限内 交于点 是以线段 为底边的等腰三角形，若双曲线 的离心率 ，则椭圆 的离心率取值范围是（ ） A. B. C. D. 【答案】C 【解析】试题分析：双曲线 的离心率 ，椭圆 的离心率为 ，选 C. 考点：椭圆、双曲线的定义及离心率 【方法点睛】解决椭圆和双曲线的离心率的求值及范围问题其关键就是确立一个关于 a，b， c 的方程或不等式，再根据 a，b，c 的关系消掉 b 得到 a，c 的关系式，建立关于 a，b，c 的方程或不等式，要充分利用椭圆和双曲线的几何性质、点的坐标的范围等. 二、填空题（每题 5 分，满分 20 分，将答案填在答题纸上） 13. 原命题“若 ，则 ”的逆否命题是__________． 【答案】若 ，则 【解析】根据逆否命题的定义，可得：若 ，则 . 14. 比较两数的大小： __________ ． 【答案】 【解析】因为 ，所以 ，故填 . 15. 抛物线 的焦点为 ，其准线与双曲线 相交于 两点，若 为 等边三角形，则 等于__________． 【答案】 【解析】抛物线的焦点坐标 ，准线方程为 ， 准线方程与双曲线联立可得 ，解得 ，因为 为等边三角形， 所以 ，即 ，即 ，解得 ，故答案为： . 16. 下列命题中 ①已知点 ，动点 满足 ，则点 的轨迹是一个圆； ②已知 ，则动点 的轨迹是双曲线右边一支； ③两个随机变量的线性相关性越强，则相关系数的绝对值就越接近于 ； ④在平面直角坐标系内，到点 和直线 的距离相等的点的轨迹是抛物线； ⑤设定点 ，动点 满足条件 ，则点 的轨迹是椭圆. 正确的命题是__________． 【答案】①②③ 【解析】①中 ，根据 ，化简得： ， 所以点 P 的轨迹是个圆；②因为 ,所以根据双曲线的的定义，P 点的 轨迹是双曲线右支，正确；③根据相关性定义，正确；④因为点在直线上，不符合抛物线定 义，错误；⑤因为 ，且当 时取等号，不符合椭圆的定义，错误.综上正确 的是①②③. 三、解答题 （本大题共 6 小题，共 70 分.解答应写出文字说明、证明过程或演 算步骤.） 17. 已知命题 直线 与抛物线 没有交点；已知命题 方程 表示双曲线；若 为真， 为假，试求实数 的取值范围. 【答案】 或 或 【解析】试题分析：当命题 为真命题时，首先由直线与抛物线没有交点可知构成的方程组 无解，从而可得到 的取值范围，当命题 为真命题时，由双曲线方程的特点可得到 的取值 范围，结合复合命题的判定方法可知两命题一真一假，从而分两种情况讨论可进行求解. 若直线 与抛物线 （ ）没有交点， 由 得 ，代入 得 ，得 ， 则由 ，解得 ， 若方程 表示双曲线，则 ，得 或 ， 若 为真， 为假，则 ， 一真一假， 若 真 假，则 得 ， 若 假 真，则 得 或 ， 综上所述 的取值范围是 或 或 . 18. 已知抛物线 与直线 相交于 两点. （1）求证： ； （2）当 的弦长等于 时，求 的值. 【答案】（1）见解析；（2） 【解析】试题分析： 证明 可有两种思路： 证 , 取 中点 ,证 求 的值，关键是利用面积建立关于 的方程，求 的面积也有两种思路： 利用 ， 设 , ,直线和 轴交点为 ，利用 . 解析： 由方程 消去 后，整理得 设 , ，由韦达定理 在抛物线 上， 设直线与 轴交点为 ，又显然 令 则 ,即 ,解得 点睛：本题考查了直线与抛物线的关系，在求三角形面积时可以采用分割的方法，沿着 轴 分割成两个三角形，这样在计算两个三角形面积时有公共底，高就可以转化为直线与抛物线 两交点纵坐标的差，再依据直线方程与抛物线方程联立，求得两交点纵坐标的差。 19. 某校高一（ ）班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污 损，可见部分如图. （1）求分数在 的频率及全班人数； （2）求分数在 之间的频数，并计算频率分布直方图中 间距形的高； （3）若要从分数在 之间的试卷中任取两份分析学生失分情况，求在抽取的试卷中， 至少有一份分数在 之间的概率. 【答案】（1）25；（2）0.012；（3）0.7 【解析】 试题分析：（Ⅰ）先由频率分布直方图求出[50，60）的频率，结合茎叶图中 得分在[50，60）的人数即可求得本次考试的总人数；（Ⅱ）根据茎叶图的数据，利用（Ⅰ） 中的总人数减去[50，80）外的人数，即可得到[50，80）内的人数，从而可计算频率分布直 方图中[80，90）间矩形的高；（Ⅲ）用列举法列举出所有的基本事件，找出符合题意得基本 事件个数，利用古典概型概率计算公式即可求出结果． （Ⅰ）分数在[50，60）的频率为 0.008×10=0.08， 由茎叶图知：分数在[50，60）之间的频数为 2， ∴全班人数为 ． （Ⅱ）分数在[80，90）之间的频数为 25﹣22=3； 频率分布直方图中[80，90）间的矩形的高为 ． （Ⅲ）将[80，90）之间的 3 个分数编号为 a1，a2，a3，[90，100）之间的 2 个分数编号为 b1，b2， 在[80，100）之间的试卷中任取两份的基本事件为： （a1，a2），（a1，a3），（a1，b1），（a1，b2），（a2，a3），（a2，b1），（a2，b2），（a3，b1），（a3，b2）， （b1，b2）共 10 个， 其中，至少有一个在[90，100）之间的基本事件有 7 个， 故至少有一份分数在[90，100）之间的概率是 ． 点睛：本题考查了茎叶图和频率分布直方图的性质，以及古典概型概率计算公式的应用，此 题是基础题． 20. 已知圆 ，点 . （1）若是从 三个数中任取的一个数， 是从 三个数中任取的一个数，求点 在圆 内的概率； （2）若是从区间 任取的一个数， 是从区间 任取的一个数，求点 在圆 外的概率. 【答案】（1） ；（2） 【解析】试题分析：（1）列举法求得所有的 共 个，而满足条件的 共 个，由古典概 型概率公式可得结果；（2）试验的所有基本事件所构成的区域为边长是 的正方形，其中所 求事件的区域为正方形内圆外的部分，由几何概型概率公式即可得到所求事件发生的概率. 试题解析：（1）用数对 表示基本事件， 则其所有可能结果有：（1，0），（1，1），（1，2），（2，0），（2，1）， （2，2）（3，0），（3，1），（3，2）共 9 个。 事件 点 在圆 内， 其结果为：（1，0），（1，1），（2，0），（2，1）共 4 个 所以 ． （2）所有可能结果 表示的区域图中正方形 , 事件 点 在圆 外表示的区域为图中阴影部分 所以 21. 已知 是椭圆 的左右焦点， 为原点， 在椭圆上，线段 与 轴的交点 满足 . （1）求椭圆的标准方程； （2）过椭圆右焦点 作直线交椭圆于 两点，交 轴于 点，若 ， 求 . 【答案】（1） ；（2） 【解析】试题分析：（1）由 知,N 为 中点，而 又为 中点，所以 为 的中位线，又由于 ，所以 ，由 P 坐标可知 ，可知 c ，在 直角三角形 中，由勾股定理得出 ，而 ，由此可求出 ，从而求 出椭圆的标准方程. （2）设出直线方程与椭圆联立，设出 ，应用韦达定理将 转化为 的关系. 试题解析：（1）因为 知,N 为 中点，而 又为 中点，所以 为 的中位线，又由于 ，所以 ，由 P 坐标可知 ，所以 ， RT 中，由勾股定理得 ，又因为 ，所以 ， 易得椭圆： （2）设 设： ，与 联立得 同理 点睛:平面几何知识的运用大大简化了本题的运算，故求解解析几何题时需充分挖掘题目的 几何关系. 22. 已知 分别是椭圆 的左、右焦点，离心率为 ， 分别是椭圆 的上、下顶点， . （1）求椭圆 的方程； （2）过 作直线与 交于 两点，求三角形 面积的最大值（ 是坐标原点）. 【答案】（1） ；（2） 【解析】试题分析：（1）根据离心率为 ， ，列出关于、 、的方程组，结合 性质 ，求出、 、，即可得椭圆 的方程；（2）直线 斜率存在，设其方程为 .，直线方程与椭圆方程联立，根据韦达定理，弦长公式、点到直线距离公式及三 角形面积公式将角形 面积用 表示，利用基本不等式 即可得结果. 试题解析：（1）由题知， ， ， ， ∴ ，∴ ，① ∵ ，∴ ，∴ ，② ①②联立解得 ， ，∴椭圆 的方程为 ． （2）设 ， ，显然直线 斜率存在，设其方程为 ， 代入 ，整理得 ， 则 ，即 ， ， ， ， 所以 到的距离 ， 所以三角形 面积 ， 设 ，所以 ， 当且仅当 ，即 ，即 ，即 时取等号， 所以 面积的最大值为 ． 【方法点晴】本题主要考查待定系数法求椭圆方程及圆锥曲线求最值，属于难题.解决圆锥 曲线中的最值问题一般有两种方法：一是几何意义，特别是用圆锥曲线的定义和平面几何的 有关结论来解决，非常巧妙；二是将圆锥曲线中最值问题转化为函数问题，然后根据函数的 特征选用参数法、配方法、判别式法、三角函数有界法、函数单调性法以及均值不等式法， 本题（2）就是用的这种思路，利用均值不等式法求三角形最值的.