命题角度2-4 应用正弦定理和余弦定理解实际问题（第01期）-2018年高考数学（文）备考之百强校大题狂练系列

命题角度2-4 应用正弦定理和余弦定理解实际问题（第01期）-2018年高考数学（文）备考之百强校大题狂练系列

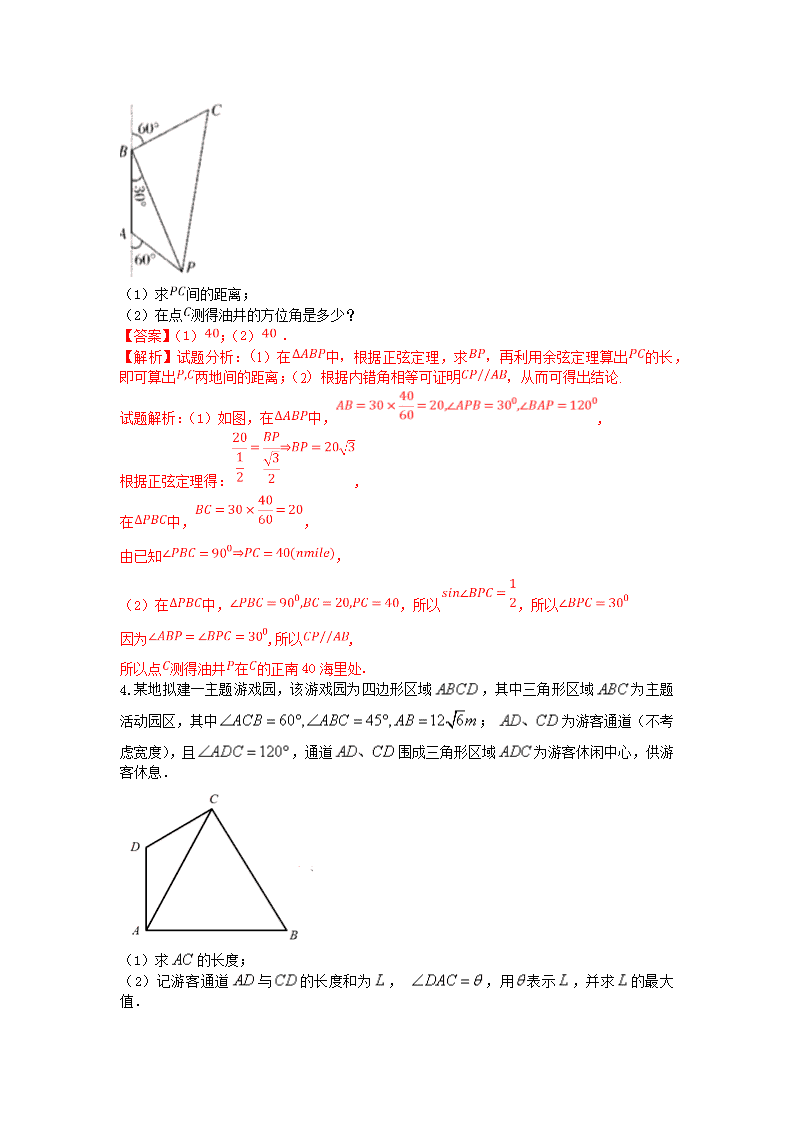
‎2018届高考数学（文）大题狂练 命题角度4：应用正弦定理和余弦定理解实际问题 ‎1.为绘制海底地貌图，测量海底两点， 间的距离，海底探测仪沿水平方向在， 两点进行测量， ， ， ， 在同一个铅垂平面内. 海底探测仪测得 ‎ 同时测得海里。 ‎ ‎（1）求AD的长度; ‎ ‎（2）求， 之间的距离.‎ ‎【答案】（1） ；（2）， 间的距离为海里. ‎ ‎（2）， ‎ ‎ ，‎ 在中，由余弦定理得， ‎ 即（海里）．‎ 答： ， ， 间的距离为海里.【来.源：全,品…中&高*考*网】‎ 点睛：解应用题，首先要增强应用数学的意识．解应用题可分两步：第一步，先分析问题，抓住实际问题中的数量关系，将其转化成一般数学问题；第二步，利用所学数学知识和方法解决这个数学问题，其中的关键在于如何将实际问题数学化，也就是说如何将实际问题等价转化为一个数学问题．‎ ‎2.某地拟建一主题游戏园，该游戏园为四边形区域，其中三角形区域为主题 活动园区，其中； 为游客通道（不考虑宽度），且，通道围成三角形区域为游客休闲中心，供游客休息． ‎ ‎【来.源：全,品…中&高*考*网】‎ ‎（1）求的长度；‎ ‎（2）记游客通道与的长度和为， ，用表示，并求的最大值．‎ ‎【答案】（1）;（2）见解析.‎ ‎【解析】试题分析：（1）利用正弦定理，求的长度．‎ ‎（2）求出，可得出关于的关系式，化简后求的最大值．‎ ‎3.某海轮以公里/小时的速度航行，在点测得海上面油井在南偏东，向北航行40分钟后到达点，测得油井在南偏东，海轮改为北偏东的航向再行驶40分钟到达点.‎ ‎（1）求间的距离；‎ ‎（2）在点测得油井的方位角是多少？‎ ‎【答案】（1）；（2） .‎ ‎【解析】试题分析：（1）在中，根据正弦定理，求，再利用余弦定理算出的长，即可算出两地间的距离；（2）根据内错角相等可证明，从而可得出结论.【来.源：全,品…中&高*考*网】‎ 试题解析：（1）如图，在中，,‎ 根据正弦定理得：,‎ 在中，，‎ 由已知，‎ ‎（2）在中，，所以，所以 因为,所以,‎ 所以点测得油井在的正南40海里处.‎ ‎4.某地拟建一主题游戏园，该游戏园为四边形区域，其中三角形区域为主题活动园区，其中； 为游客通道（不考虑宽度），且，通道围成三角形区域为游客休闲中心，供游客休息． ‎ ‎（1）求的长度；‎ ‎（2）记游客通道与的长度和为， ，用表示，并求的最大值．‎ ‎【答案】（1）;（2）见解析.‎ ‎【解析】试题分析：（1）利用正弦定理，求的长度．‎ ‎（2）求出，可得出关于的关系式，化简后求的最大值．‎ ‎5.如图所示， 是某海湾旅游区的一角，为营造更加优美的旅游环境，旅游区管委会决定建立面积为平分千米的三角形主题游戏乐园，并在区域建立水上餐厅.‎ 已知， .‎ ‎（1）设， ，用表示，并求的最小值；‎ ‎（2）设（为锐角），当最小时，用表示区域的面积，并求的最小值.‎ ‎【答案】(1) ;(2)S= ,8－.‎ ‎【解析】试题分析：‎ ‎(1)首先确定函数的解析式为结合均值不等式的结论可得的最小值是;‎ ‎(2)结合题意和三角函数的性质可得S=，利用三角函数的性质可知的最小值是8－.‎ 试题解析：‎ ‎（1）由S△ACB＝AC·BC·sin∠ACB＝4得，BC＝，‎ 在△ACB中，由余弦定理可得，AB2＝AC2＋BC2－2AC·BC·cos∠ACB，‎ 即y2＝x 2＋＋16，‎ 所以y＝‎ y＝≥＝4，‎ 当且仅当x2＝，即x＝4时取等号．‎ 所以当x＝4时，y有最小值4．‎ ‎6.如图所示，某工厂要设计一个三角形原料，其中.‎ ‎（1）若，求的面积的最大值；‎ ‎（2）若的面积为，问为何值时取得最小值.‎ ‎【答案】（1）；（2）时， 有最小值，即最小.‎ ‎【解析】试题分析：（1）建系设点，根据条件求出A的轨迹方程，则三角形的高为圆上动点到直线的距离，数形结合可求三角形面积的最大值．（2）设，表示出三角形面积，求出BC= ，利用导数求其最值即可.‎ ‎ 【来.源：全,品…中&高*考*网】‎ ‎（2）设，由得.‎ 令， ‎ 令得，列表：略. 在上单调递减，‎ 在上单调递增，当时， 有最小值，即最小. ‎ 试题点睛：本题主要考查了三角形面积公式，余弦定理以及导数的概念及其应用，考查了转化思想和数形结合思想的应用，属于中档题． ‎