- 2021-06-23 发布 |
- 37.5 KB |
- 6页

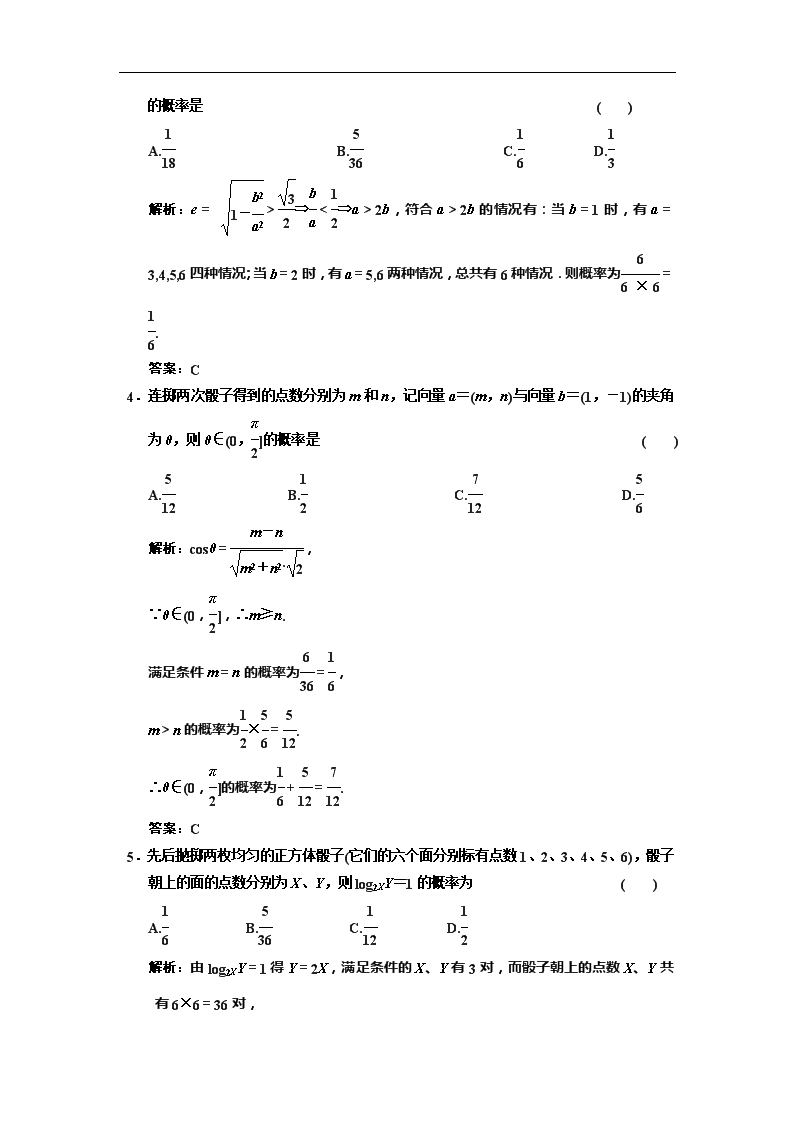

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考数学专题复习练习第十一章 第二节 古典概型[文]
第十一章 第五节 古典概型[理] 课下练兵场 命 题 报 告 难度及题号 知识点 容易题 (题号) 中等题 (题号) 稍难题(题号) 简单的古典概型问题 1、2、5 7、8、9、10 复杂事件的古典概型问题 3 4、6 11、12 一、选择题 1.某班准备到郊外野营,为此向商店定了帐篷,如果下雨与不下雨是等可能的,能否准时收到帐篷也是等可能的,只要帐篷如期运到,他们就不会淋雨,则下列说法正确的是 ( ) A.一定不会淋雨 B.淋雨的可能性为 C.淋雨的可能性为 D.淋雨的可能性为 解析:基本事件有“下雨帐篷到”“不下雨帐篷到”“下雨帐篷未到”“不下雨帐篷未到”4种情况,而只有“下雨帐篷未到”时会淋雨,故淋雨的可能性为. 答案:D 2.有一对酷爱运动的年轻夫妇给他们12个月大的婴儿3块分别写有“20”,“08”和“北京”的字块,如果婴儿能够排成“2008北京”或者“北京2008”,则他们就给婴儿奖励. 假设婴儿能将字块横着正排,那么这个婴儿能得到奖励的概率是 ( ) A. B. C. D. 解析:“20”,“08”,“北京”三字块的排法共有“2008北京”、“20北京08”、“0820北京”、“08北京20”、“北京2008”、“北京0820”6种情况,而得到奖励的情况有2种,故婴儿能得到奖励的概率为=. 答案:C 3.某同学同时掷两颗骰子,得到点数分别为a,b,则椭圆+=1(a>b>0)的离心率e>的概率是 ( ) A. B. C. D. 解析:e= >⇒<⇒a>2b,符合a>2b的情况有:当b=1时,有a= 3,4,5,6四种情况;当b=2时,有a=5,6两种情况,总共有6种情况.则概率为=. 答案:C 4.连掷两次骰子得到的点数分别为m和n,记向量a=(m,n)与向量b=(1,-1)的夹角为θ,则θ∈(0,]的概率是 ( ) A. B. C. D. 解析:cosθ=, ∵θ∈(0,],∴m≥n. 满足条件m=n的概率为=, m>n的概率为×=. ∴θ∈(0,]的概率为+=. 答案:C 5.先后抛掷两枚均匀的正方体骰子(它们的六个面分别标有点数1、2、3、4、5、6),骰子朝上的面的点数分别为X、Y,则log2XY=1的概率为 ( ) A. B. C. D. 解析:由log2XY=1得Y=2X,满足条件的X、Y有3对,而骰子朝上的点数X、Y共有6×6=36对, ∴概率为=. 答案:C 6.[理]电子钟一天显示的时间是从00∶00到23∶59,每一时刻都由四个数字组成,则一天中任一时刻显示的四个数字之和为23的概率为 ( ) A. B. C. D. 解析:电子钟显示时刻可设为AB∶CD, 其中A=0,1,2,B=0,1,2,3,…,9,C=0,1,2,3,…,5,D=0,1,2,3,…,9. (1)当A=0时,B,C,D可分别为9、5、9一种情况; (2)当A=1时,B,C,D可分别为9、4、9或9、5、8或8、5、9三种情况; (3)当A=2时,不存在.∴符合题意的只有4种, 显示的所有数字和数为: A=0时,10×6×10=600; A=1时,10×6×10=600; A=2时,4×6×10=240. ∴P==. 答案:C [文]已知一组抛物线y=ax2+bx+1,其中a为2,4,6,8中任取的一个数,b为1,3,5,7中任取的一个数,从这些抛物线中任意抽取两条,它们在与直线x=1交点处的切线互相平行的概率是 ( ) A. B. C. D. 解析:抛物线只有4×4=16(条),从中任取两条有120(种)不同取法,∵y′=ax+b在x=1处的斜率为a+b.故符合a+b=3,只有0对,a+b=5共有1对,a+b=7有3对,a+b=9有6对,a+b=11有3对,a+b=13只有1对,∴共有14对,P==. 答案:B 二、填空题 7.在5个数字1、2、3、4、5中,若随机取出三个数字,则剩下两个数字都是奇数的概率是________(结果用数值表示). 答案: 8.假设小军、小燕和小明所在的班级共有50名学生,并且这50名学生早上到校先后的可能性相同,则“小燕比小明先到校,小明又比小军先到校”的概率为__________. 解析:将3人排序共包含6个基本事件, 由古典概型得P=. 答案: 9.任取一个三位正整数N,则对数log2N是一个正整数的概率是__________. 解析:∵26=64,27=128,28=256,29=512,210=1 024, ∴满足条件的正整数只有27,28,29三个, ∴所求的概率P==. 答案: 三、解答题 10.[理]某考生参加一所大学自主招生考试,面试时从一道数学题,两道自然科学类题,三道社科类题中任选两道回答,且该生答对每一道数学、自然科学、社科类试题的概率依次为0.6、0.7、0.8. (1)求该考生恰好抽到两道社科类试题的概率; (2)求该考生抽到的两道题属于不同学科类并且都答对的概率. 解:(1)P===. (2)该考生抽到一道数学题,一道自然科学类题的概率为P1==; 该考生抽到一道数学题,一道社科类试题的概率为 P2==; 该考生抽到一道自然科学类题,一道社科类试题的概率为P3==. 故该考生抽到的两道题属于不同学科类并且都答对的概率为P=×0.6×0.7+×0.6×0.8+×0.7×0.8=0.376. [文]为了了解《中华人民共和国道路交通安全法》在学生中的普及情况,调查部门对某校6名学生进行问卷调查,6人得分情况如下: 5,6,7,8,9,10. 把这6名学生的得分看成一个总体. (1)求该总体的平均数; (2)用简单随机抽样方法从这6名学生中抽取2名,他们的得分组成一个样本.求该样本平均数与总体平均数之差的绝对值不超过0.5的概率. 解:(1)总体平均数为 (5+6+7+8+9+10)=7.5. (2)设A表示事件“样本平均数与总体平均数之差的绝对值不超过0.5”.从总体中抽取2个个体全部可能的基本结 果有:(5,6),(5,7),(5,8),(5,9),(5,10),(6,7),(6,8),(6,9),(6,10),(7,8),(7,9),(7,10),(8,9),(8,10),(9,10),共15个基本结果.事件A包括的基本结果有:(5,9),(5,10),(6,8),(6,9),(6,10),(7,8),(7,9),共有7个基本结果. 所以所求的概率为P(A)=. 11.(2010·银川模拟)把一颗骰子投掷2次,观察出现的点数,并记第一次出现的点数为a,第二次出现的点数为b,试就方程组解答下列各题: (1)求方程组只有一个解的概率; (2)求方程组只有正数解的概率. 解:事件(a,b)的基本事件有36个. 由方程组可得 (1)方程组只有一个解,需满足2a-b≠0, 即b≠2a,而b=2a的事件有(1,2),(2,4),(3,6)共3个,所以方程组只有一个解的概率 为P1=1-=. (2)方程组只有正数解,需2a-b≠0且 即 或 其包含的事件有13个:(2,1),(3,1),(4,1),(5,1),(6,1),(2,2),(3,2),(4,2),(5,2), (6,2),(1,4),(1,5),(1,6). 因此所求的概率为. 12.已知关于x的一元二次函数f(x)=ax2-bx+1,设集合P={1,2,3},Q={-1,1,2,3,4,},分别从集合P和Q中随机取一个数作为a和b. (1)求函数y=f(x)有零点的概率; (2)求函数y=f(x)在区间[1,+∞)上是增函数的概率. 解:(a,b)共有(1,-1),(1,1),(1,2),(1,3),(1,4),(2,-1),(2,1),(2,2),(2,3),(2,4),(3,-1),(3,1),(3,2),(3,3),(3,4),15种情况. (1)若函数y=f(x)有零点,则需Δ=b2-4a≥0. 有(1,2),(1,3),(1,4),(2,3),(2,4),(3,4),6种情况, 所以函数y=f(x)有零点的概率为=. (2)若函数y=f(x)在区间[1,+∞)上是增函数,需对称轴x=≤1. 有(1,-1),(1,1),(1,2),(2,-1),(2,1),(2,2),(2,3),(2,4),(3,-1),(3,1),(3,2),(3,3),(3,4),13种情况. 所以函数y=f(x)在区间[1,+∞)上是增函数的概率为.查看更多