江苏省扬州中学2020届高三上学期11月考试 数学

江苏省扬州中学2020届高三上学期11月考试 数学

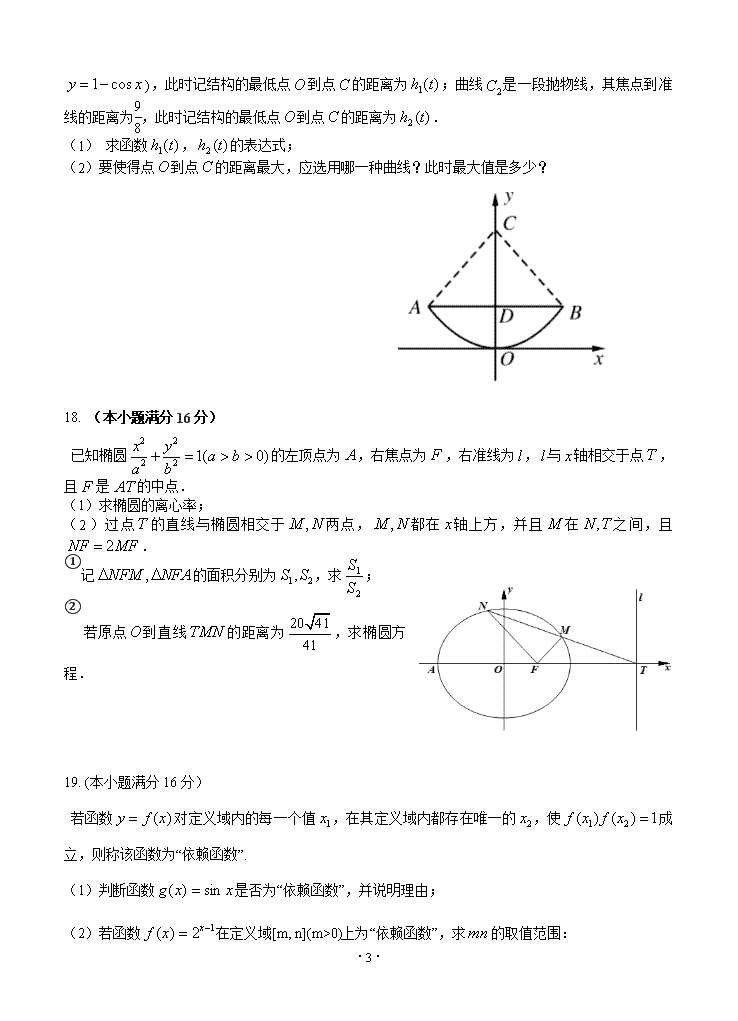
扬州中学高三数学11月考 2019.11.1‎ ‎ 数学Ⅰ试题 一、填空题（每小题5分，计70分）‎ ‎1．已知集合则 ．‎ ‎2.设幂函数的图像经过点，则 ．‎ ‎3.已知复数（为虚数单位），则复数的共轭复数为 .‎ 4. 若双曲线的虚轴长为2，则实数的值为________．‎ 5. 已知,则“”是直线与直线平行的 条件（从“充分不必要"、“必要不充分”、“充分必耍”、“既不充分也不必要“中选择恰当的一个填空）.‎ ‎6. 已知实数满足条件，则的取值范围是__________．‎ ‎7..若，则 ．‎ ‎8.设函数，则不等式的解集为 .‎ ‎9.已知直线与曲线切于点,且直线与函数的图象交于点.若，则的值为 .‎ ‎（第10题）‎ ‎10.如图，在圆：上取一点，为 轴上的两点，且，延长，分别与圆交于点，则直线的斜率为 ． ‎ ‎11.若直线上存在相距为的两个动点，圆上存在点，使得为等腰直角三角形（为直角顶点），则实数的取值范围为 .‎ ‎·15·‎ ‎12.在四边形中，AB＝6，AD＝2，＝，AC与BD相交于点O，E是BD的中点，·＝8，则·＝________．‎ ‎13.若，均为正实数，则的最小值为_______.‎ ‎14.给出函数，这里，若不等式恒成立，为奇函数，且函数恰有两个零点，则实数的取值范围为________________．‎ 二、解答题（共6道题，计90分）‎ ‎15、（本小题满分14分）‎ 如图，已知A、B、C、D四点共面，且CD=1，BC=2，AB=4，，.‎ ‎（1）求;（2）求AD.‎ ‎16.（本小题满分14分）‎ 已知圆的圆心为，直线.‎ ‎（1）若，求直线被圆所截得弦长的最大值；‎ ‎（2）若直线是圆心下方的切线，当在的变化时，求的取值范围．‎ ‎17. （本小题满分14分）‎ 江苏省第十九届运动会在扬州举行，为此，扬州某礼品公司推出一系列纪念品，其中一个工艺品需要设计成如图所示的一个结构(该图为轴对称图形)，其中的支撑杆由长为3的材料弯折而成，边的长为，(另外用彩色线连结，此处不计)；支撑杆曲线拟从以下两种曲线中选择一种：曲线是一段余弦曲线(在如图所示的平面直角坐标系中，其表达式为 ‎·15·‎ ‎)，此时记结构的最低点到点的距离为；曲线是一段抛物线，其焦点到准线的距离为，此时记结构的最低点到点的距离为．‎ ‎（1） 求函数，的表达式；‎ ‎（2）要使得点到点的距离最大，应选用哪一种曲线？此时最大值是多少？‎ ‎18. （本小题满分16分）‎ ‎ 已知椭圆的左顶点为，右焦点为，右准线为，与轴相交于点，且是的中点．‎ ‎（1）求椭圆的离心率；‎ ‎（2）过点的直线与椭圆相交于两点，都在轴上方，并且在之间，且．‎ ‎①记的面积分别为，求；‎ ‎②若原点到直线的距离为，求椭圆方程．‎ ‎19. (本小题满分16分）‎ ‎ 若函数对定义域内的每一个值，在其定义域内都存在唯一的，使成立，则称该函数为“依赖函数”.‎ ‎（1）判断函数是否为“依赖函数”，并说明理由；‎ ‎（2）若函数在定义域[m, n](m>0)上为“依赖函数”，求的取值范围：‎ ‎·15·‎ ‎（3）己知函数在定义域上为“依赖函数”，若存在实数，使得对任意的,不等式都成立，求实数的最大值.‎ ‎20．（本小题满分16分）‎ 已知函数．‎ ‎（1）当时，求函数的极值；‎ ‎（2）设函数在处的切线方程为，若函数是上 的单调增函数，求的值； ‎ ‎（3）是否存在一条直线与函数的图象相切于两个不同的点？并说明理由． ‎ ‎ ‎ 数学Ⅱ(附加题)‎ 1、 已知二阶矩阵有特征值，其对应的一个特征向量为，并且矩阵对应的变换将点（1，2）变换成点（8，4），求矩阵．‎ 2、 在直角坐标系xOy中，以坐标原点O为极点，以x轴的正半轴为极轴，建立极坐标系，直线l的极坐标方程为，设点P是曲线上的动点，求P到直线l距离的最大值.‎ ‎·15·‎ ‎3、现有一款智能学习APP，学习内容包含文章学习和视频学习两类，且这两类学习互不影响．已知该APP积分规则如下：每阅读一篇文章积1分，每日上限积5分；观看视频累计3分钟积2分，每日上限积6分．经过抽样统计发现，文章学习积分的概率分布表如表1所示，视频学习积分的概率分布表如表2所示．‎ ‎（1）现随机抽取1人了解学习情况，求其每日学习积分不低于9分的概率；‎ ‎（2）现随机抽取3人了解学习情况，设积分不低于9分的人数为，求的概率分布及数学期望．‎ ‎4、数列满足且.‎ ‎（1）用数学归纳法证明：；‎ ‎（2）已知不等式对成立，证明：（其中无理数）.‎ 扬州中学高三数学月考 2019.11.1‎ ‎ 试题Ⅰ 一、填空题（每小题5分，计70分）‎ ‎1. 2. 3. 4. 5.充分必耍6.[2，3]7.8.9.‎ ‎·15·‎ ‎10.解析：.由题意，取,,因为，所以，过原点所以，所以 ‎11.‎ ‎12. －　解析：由＝得DC∥AB，且DC＝2，则△AOB∽△COD，所以＝＝＝＋.因为E是BD的中点，所以＝＋，所以·＝·＝||2＋||2＋·＝＋＋·＝8，所以·＝4，所以·＝·(－)＝||2－||2－·＝4－×36－×4＝－.‎ ‎13.解析：‎ 当，即时取得最小值为：‎ ‎·15·‎ ‎14.[－2，0)∪[4，＋∞)‎ 二、解答题（共6道题，计90分）‎ ‎15、‎ ‎16. 解析：（1）已知圆的标准方程是（x＋a）2＋（y－a）2＝4a（0＜a≤4），‎ ‎·15·‎ 则圆心C的坐标是（－a，a），半径为2. ‎ 直线l的方程化为：x－y＋4＝0.‎ 则圆心C到直线l的距离是＝|2－a|.‎ 设直线l被圆C所截得弦长为L，由圆、圆心距和圆的半径之间关系是：‎ L＝2 ‎ ‎＝2＝2.‎ ‎∵0＜a≤4，∴当a＝3时，L的最大值为 ‎ ‎（2）因为直线l与圆C相切，则有＝2， ‎ 即|m－2a|＝2.‎ 又点C在直线l的上方，∴a＞－a＋m，即2a＞m. ‎ ‎∴2a－m＝2，∴m＝－1.‎ ‎∵0＜a≤4，∴0＜≤2.‎ ‎∴m∈ ‎ ‎17. 解析： (1)对于曲线C1，因为曲线AOB的表达式为y＝1－cos x，‎ 所以点B的坐标为(t，1－cos t)，‎ 所以点O到AB的距离为1－cos t.‎ 因为DC＝3－2t，‎ 所以h1(t)＝(3－2t)＋(1－cos t)＝－2t－cos t＋4；‎ 对于曲线C2，设C2：x2＝2py，由题意得p＝，‎ 故抛物线的方程为x2＝y，即y＝x2，‎ 所以点B的坐标为，‎ 所以点O到AB的距离为t2.‎ 因为DC＝3－2t，‎ 所以h2(t)＝t2－2t＋3.‎ ‎(2)因为h′1(t)＝－2＋sin t<0，‎ 所以h1(t)在上单调递减，‎ 所以当t＝1时，h1(t)取得最大值2－cos 1.‎ 因为h2(t)＝＋，1≤t≤，‎ 所以当t＝1时，h2(t)取得最大值为.‎ ‎·15·‎ 因为2－cos 1≈1.46＞，‎ 所以选用曲线C1，且当t＝1时，点O到点C的距离最大，最大值为2－cos 1.‎ ‎18. （1）因为是的中点，所以，即，又、，所以，所以； ‎ ‎（2）①过作直线的垂线，垂足分别为，则，又，故，故是的中点，∴， 又是中点，∴，∴； ‎ ‎②解法一：设，则椭圆方程为，‎ 由①知是的中点，不妨设，则，‎ 又都在椭圆上，即有即，两式相减得，解得，可得， 故直线的斜率为，‎ 直线的方程为，即 ‎ 原点到直线的距离为，‎ ‎·15·‎ 依题意，解得，故椭圆方程为． ‎ 解法二：设，则椭圆方程为，‎ 由①知是的中点，故，‎ 直线的斜率显然存在，不妨设为，故其方程为，与椭圆联立，并消去得：，整理得，（*）‎ 设，，依题意 由解得 ‎ 所以，解之得，即．‎ 直线的方程为，即 ‎ 原点到直线的距离为，‎ 依题意，解得，故椭圆方程为． ‎ ‎19．解：(1) 对于函数的定义域R内存在，则 无解 故不是“依赖函数”； …3分 ‎ (2) 因为在[m，n]递增，故f(m)f(n)=1，即 ……5分 由n>m>0，故，得0

查看更多