陕西省渭南市2020届高三上学期期末考试数学文科试题

陕西省渭南市2020届高三上学期期末考试数学文科试题

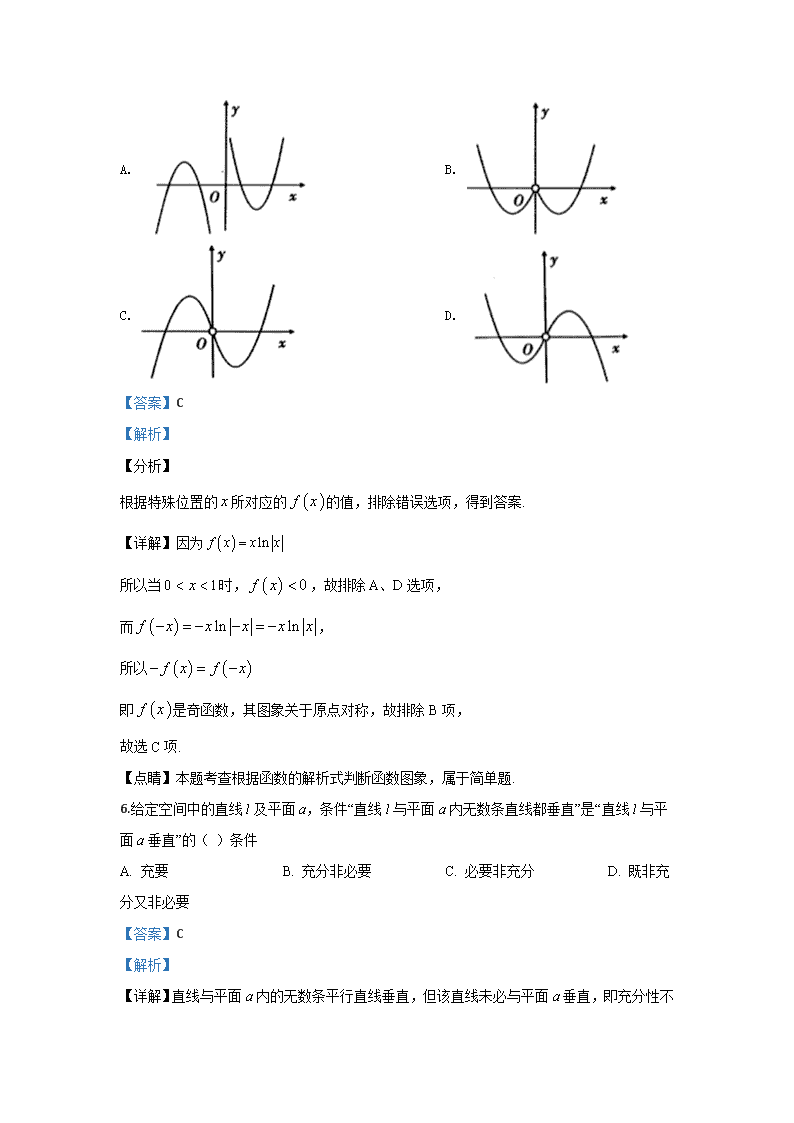
渭南市 2020 年高三教学质量检测 数学试题（文科） 一、选择题：本大题共 12 小题，每小题 5 分，共 60 分.在每小题列出的四个选 项中，选出符合题目要求的一项. 1.设全集 ，集合 ， ，则集合 ( ) A. B. C. D. 【答案】B 【解析】 【分析】 根据集合补集与交集定义求结果. 【详解】 ， 所以 故选 B 【点睛】本题考查集合补集与交集定义，考查基本求解能力，属基本题. 2.已知 i 为虚数单位,若 ,（a,b∈R）,则 a+b=（ ） A. 1 B. C. D. 2 【答案】A 【解析】 【分析】 利用复数代数形式的乘除运算化简，再由复数相等的条件求得 a 与 b 的值，则答案可求． 【详解】解：由 ， 得 a＝b ， ∴a+b＝1． 故选：A． 【点睛】本题考查复数代数形式的乘除运算，考查复数相等的条件，是基础题． U = R { | 0 2}A x x= < < { 3, 1,1, 3}B = − − ( )U A B = { 3, 1}− − { 3, 1, 3}− − {1, 3} { }1,1− U A = { | 0 2}x x x或≤ ≥ ( )U A B∩ = { }3, 1,3− − 1 1 a bii = +− 2 2 2 ( )( ) 1 1 1 1 1 1 1 2 2 i i a bii i i += = + = +− − + 1 2 = 3.向量 满足 则向量 与 的夹角为（ ） A. B. C. D. 【答案】C 【解析】 试题分析：由已知可得 夹角为 ，故选 C． 考点：向量的基本运算． 4.某中学有高中生 人，初中生 人，男、女生所占的比例如下图所示.为了解学生 的学习情况，用分层抽样的方法从该校学生中抽取一个容量为 的样本，已知从高中生中抽 取女生 人，则从初中生中抽取的男生人数是（ ） A. B. C. D. 【答案】A 【解析】 分析：首先确定分层抽样的抽取比例，然后求解初中生中抽取的男生人数即可. 详解：因为分层抽样的抽取比例为 ， 所以初中生中抽取的男生人数是 人. 本题选择 A 选项. 点睛：进行分层抽样的相关计算时，常利用以下关系式巧解： (1) ； (2)总体中某两层的个体数之比＝样本中这两层抽取的个体数之比． 5.函数 的大致图象是（ ） ,a b 1, 2,( ) (2 ),a b a b a b= = + ⊥ − a b 45° 60° 90° 120° 2 2( )(2 ) 2 0a b a b a a b b a b a b+ − = + ⋅ − = ⋅ = ⇒ ⊥ ⇒           90° 3000 2000 n 21 12 15 20 21 21 1 3000 0.7 100 =× 2000 0.6 12100 × = n N =样本容量 该层抽取的个体数 总体的个数 该层的个体数 ( ) lnf x x x= A. B. C. D. 【答案】C 【解析】 【分析】 根据特殊位置的 所对应的 的值，排除错误选项，得到答案. 【详解】因为 所以当 时， ，故排除 A、D 选项， 而 ， 所以 即 是奇函数，其图象关于原点对称，故排除 B 项， 故选 C 项. 【点睛】本题考查根据函数的解析式判断函数图象，属于简单题. 6.给定空间中的直线 l 及平面 a，条件“直线 l 与平面 a 内无数条直线都垂直”是“直线 l 与平 面 a 垂直”的（ ）条件 A. 充要 B. 充分非必要 C. 必要非充分 D. 既非充 分又非必要 【答案】C 【解析】 【详解】直线与平面 a 内的无数条平行直线垂直，但该直线未必与平面 a 垂直，即充分性不 x ( )f x ( ) lnf x x x= 0 1x< < ( ) 0f x < ( ) ln lnf x x x x x− = − − = − ( ) ( )f x f x− = − ( )f x 成立. 直线 l 与平面 a 垂直，则直线 l 与平面 a 内任意直线都垂直，所以直线 l 与平面 a 内无数条 直线都垂直，必要性成立，选 C. 【此处有视频，请去附件查看】 7.已知函数 是偶函数，则在 上此函数 A. 是增函数 B. 不是单调函数 C. 是减函数 D. 不能确 定 【答案】A 【解析】 【分析】 先由函数为偶函数求得 ，进而由抛物线的性质可得解. 【详解】因为函数 是偶函数，所以函数图像关于 轴对称， 即 ，解得 . 所以 为开口向下的抛物线，所以在 上函数单调递增. 故选 A. 【点睛】本题主要考查了函数奇偶性的性质及二次函数的单调性，属于基础题. 8.设函数 与直线 的交点的横坐标构成以 为公差的等差数列，且 是 图象的一条对称轴，则下列区间中是函数的单调递减 区间的是 A. B. C. D. 【答案】D 【解析】 2( ) ( 1) 2 3f x m x mx= − − + ( ,0)−∞ 0m = 2( ) ( 1) 2 3f x m x mx= − − + y 01 m m =− 0m = 2( ) 3f x x= − + ( ,0)−∞ ( )= sin( )( 0, 0, )2f x A x A πω ϕ ω ϕ+ > > ≤ 3y = π 6x π= ( )f x [ ,0]3 π− 4 5[ , ]3 6 π π− − 2 7[ , ]3 6 π π 5[ , ]6 3 π π− − 因为函数 与直线 的交点的横坐标构成以 为公差的等差数列，所以函数 的周期为 ，求得 ，且 ，再由 ， 求 得 结 合 ， 可 得 ， 令 ， 求 得 ，故函数的增区间为 ，令 可得 ， ， 是增区间，可排除选项 ，故选 D. 9.已知离心率为 的双曲线 的右焦点为 F,直线 l 过点 F 且垂直于 x 轴,若 l 被 抛物线 截得的线段长为 4,则 p=（ ） A. 1 B. 2 C. D. 【答案】B 【解析】 【分析】 先求出双曲线的焦点坐标，推出直线方程，代入抛物线中，求出 y，根据 l 被抛物线 y2＝2px 截得的线段长为 4，即可求出 p，问题得以解决． 【详解】解：离心率为 的双曲线 1，可得 e ， 解得 a ，c 1， 双曲线 1 的右焦点为 F（1，0）， ∵直线 l 过点（1，0）且垂直于 x 轴， ∴x＝1， ( ) ( )= sin ( 0, 0, )2f x A x A πω ϕ ω ϕ+ > > ≤ 3y = π ( )f x 2π πω = 2ω = 3A = 2 ,6 2k k Z π πϕ π× + = + ∈ 6k πϕ π= + 2 πϕ < ( ), 3 26 6f x sin x π πϕ  = ∴ = +   2 2 22 6 2k x k π π ππ π− ≤ + ≤ + 3 6k x k π ππ π− ≤ ≤ + , ,3 6k k k Z π ππ π − + ∈   0, 1,1k = − ,03 π −   4 5,3 6 π π − −   2 7,3 6 π π     , ,A B C 2 2 2 2 2 1x ya − = 2 2y px= 1 2 2 2 2 2 2 2x ya − = 2 1 2 2 ac a a + = = = 2 2 = 2 1 2a= + = 2 2 2 2x ya − = 代入到 y2＝2px，可得 y2＝2p，显然 p＞0， ∴y＝± ， ∵l 被抛物线 y2＝2px 截得的线段长为 4， ∴ 2， 解得 p＝2， 故选：B． 【点睛】本题考查了双曲线的简单性质以及直线与抛物线的位置关系，属于基础题． 10.一位老师有两个推理能力很强的学生甲和乙,他告诉学生他手里拿着与以下扑克牌中的一 张相同的牌: 黑桃:3,5,Q,K 红心:7,8,Q 梅花:3,8,J,Q 方块:2,7,9 老师只给甲同学说这张牌的数字（或字母）,只给乙同学说这张牌的花色,接着老师让这两个 同学猜这是张什么牌: 甲同学说:我不知道这是张什么牌,乙同学说:我知道这是张什么牌. 甲同学说:现 我们知道了. 则这张牌是（ ） A. 梅花 3 B. 方块 7 C. 红心 7 D. 黑桃 Q 【答案】B 【解析】 【分析】 根据老师告诉甲牌的点数，告诉乙的是花色，结合甲乙对话进行推理判断即可． 【详解】解：甲不知道，说明通过数字不能判断出来，因此排除有单一数字的牌：黑桃 5,K,梅花 J，方块 2,9．而乙知道牌的颜色,如果是方片的话,即可断定是方片 7, 故选:B 【点睛】本题主要考查合情推理的应用，结合甲乙了解的情况进行推理是解决本题的关 键．考查学生的推理分析能力． 11.曲线 在 处的切线的倾斜角为 ，则 的值为（ ） A. B. C. D. 【答案】D 在 2p 2p = 2lny x x = − 1x = α cos(2 )2 πα + 4 5 4 5 − 3 5 3 5- 【解析】 【分析】 根据已知条件，求出切线斜率 ，再根据同角三角函数的基本关系可求出 ， ，从而根据二倍角公式和诱导公式求得结果. 【详解】根据已知条件， ，因为曲线 在 处的切线的倾斜 角 为 ， 所 以 ， . 因 为 ， ， 则 解 得 ， ， 故 . 故本题正确答案为 D. 【点睛】本题主要考查导数的概念及其几何意义，考查同角三角函数的基本关系和二倍角公 式，熟记公式和概念是关键，属基础题. 12.唐代诗人李颀的诗《古从军行》开头两句说：“白日登山望烽火，黄昏饮马傍交河.”诗 中隐含着一个有趣的数学问题——“将军饮马”问题，即将军在观望烽火之后从山脚下某处 出发，先到河边饮马后再回到军营，怎样走才能使总路程最短？在平面直角坐标系中，设军 营所在区域为 ，若将军从点 处出发，河岸线所在直线方程为 ， 并假定将军只要到达军营所在区域即回到军营，则“将军饮马”的最短总路程为（ ） A. B. C. D. 【答案】A 【解析】 【分析】 先求出点 A 关于直线 的对称点 ，点 到圆心的距离减去半径即为最短. 【详解】解：设点 A 关于直线 的对称点 ， 的中点为 ， tan 3α = sinα cosα 2 1 2( )f x x x ′ = + 2lny x x = − 1x = α tan (1) 1 2 3fα ′= = + = 0 2 πα< < 2 2sin cos 1a α+ = sintan 3cos αα α= = 3sin 10 α = 1cos 10 α = 3cos(2 ) sin 2 2sin cos2 5 πα α α α+ = − = − = − 2 2 1x y+ ≤ (2,0)A 3x y+ = 10 1− 2 2 1− 2 2 10 3x y+ = A′ A′ 3x y+ = ( , )A a b′ AA′ 2( , )2 2 a b+ AA bk a 2′ = − 故 解得 ， 要使从点 A 到军营总路程最短， 即为点 到军营最短的距离， “将军饮马”的最短总路程为 ， 故选 A. 【点睛】本题考查了数学文化问题、点关于直线 对称问题、点与圆的位置关系等等，解决 问题的关键是将实际问题转化为数学问题，建立出数学模型，从而解决问题. 二、填空题：本大题共 4 小题，每小题 5 分，共 20 分. 13.若变量 x,y 满足约束条件 ,则 z=x+2y 的最大值为_______ 【答案】3 【解析】 【分析】 由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合可得最优解，求出最优 解的坐标，代入目标函数得答案． 【详解】解：画出约束条件表示的可行域， 将目标函数 z＝x+2y 平移， 当目标函数经过 x﹣y＝6 和 2x+y＝9 的交点（5，﹣1）时， 的 •( 1) 12 2 32 2 b a a b  − = − − + + = 3 1 a b =  = A′ 2 23 1 1 10 1+ − = − 3 2 9 6 9 x y x y +  − ≤ ≤ ≤ ≤ z 有最大值，即：3， 故答案为：3． 【点睛】本题考查简单线性规划的应用，考查分析问题解决问题的能力，考查了数形结合的 解题思想方法，是中档题． 14.已知函数 （a>0,a≠1）与函数 y=b（b>0）存在两个不同的交点,两交点的横坐 标分别为 x1,x2（x1b>0）的顶点到直线 l1:y=x 的距离分别为 和 . （1）求椭圆 C 的标准方程 （2）设平行于 l1 的直线 l 交 C 于 A,B 两点,且 ,求直线 l 的方程. 【答案】（1） （2）直线 的方程为 或 【解析】 【分析】 7 10P = 2 2 2 2 1x y a b + = 2 2 2 OA OB AB+ =   2 2 14 x y+ = l 2 10 5y x= + 2 10 5y x= − （1）根据直线 l1 的方程可知其与两坐标轴的夹角均为 45°，进而得到 a ， b ，即可求出 C 的方程； （2）设出直线 l 的方程，与椭圆方程联立，利用根与系数的关系结合| |＝| |可 得 0，求出 t 即可. 【详解】解：（1）由直线 的方程知，直线 与两坐标轴的夹角均为 ， 故长轴端点到直线 的距离为 ，短轴端点到直线 的距离为 所以 a ， b ，解得 a＝2，b＝1， 所以椭圆 的标准方程为 （2）依题设直线 由 得： 判别式 解得 设 由韦达定理得： 由 ，故 ， 设原点为 ， ，故 ， 所以 ，即 解得： ，满足 且 ， 2 2 2= 2 2 2 2 = OA OB+  AB 2 24 4 4 5 5 t tOA OB − −⋅ = + =  1l 1l 45° 1l 2 2 a 1l 2 2 b 2 2 2= 2 2 2 2 = C 2 2 14 x y+ = : ( 0)l y x t t= + ≠ 2 2 14 y x t x y = + + = 2 25 8 4 4 0x tx t+ + − = ( )2 264 16 5 1 0t t∆ = − × − > 5 5t− < < ( ) ( )1 1 2 2A x y B x y， ， ， 1 2 2 1 2 8 5 4 4 5 tx x tx x  + = − − = ( )( ) ( ) 2 2 1 2 1 2 1 2 1 2 4 5 ty y x t x t x x x x t t −= + + = + + + = O OA OB AB+ =   OA OB⊥ 0OA OB⋅ =  2 2 1 2 1 2 4 4 4 05 5 t tx x y y − −+ = + = 2 10 5t = ± 5 5t− < < 0t ≠ 故所求直线 的方程为 或 【点睛】本题考查椭圆方程的标准方程，考查直线与椭圆的位置关系，向量和差关系与位置 关系的联系等，属于中档题． 21.设函数 . （1）求 f（x）的单调区间. （2）当 x>0 时,不等式 恒成立,（其中 为 f（x）的导函数）.求整 数 k 的最大值. 【答案】（1）函数 在 单调递减（2） 的最大值为 【解析】 【分析】 （1）求导后，解不等式即可得解； （2）问题转化为 ，令 ，则 k＜g（x）min，求函数 g（x）的 最小值即可． 【详解】解：（1）函数 的定义域是 ， ， 当 时， ， ； 当 时， ， ； 当 时， . ∴函数 在 上单调递减，即 为其单调递减区间. （2）∵ ,故 , 又 ,∴ 令 ,则 , 由 ， 令 ， l 2 10 5y x= + 2 10 5y x= − 21( ) (1 ) 2 xf x x e x= − + 2( ) '( )x k f x x x− < + '( )f x ( )f x ( )−∞ + ∞， k 2 1 1x xk xe + +−＜ ( ) 1 1x xg x xe += +− 21( ) (1 ) 2 xf x x e x= − + R ( )( ) 1xf x x e′ = − − 0x > e 1x > ( ) 0f x′ < 0x < 1xe < ( ) 0f x′ < 0x = ( ) 0f x′ = ( )f x ( )−∞ + ∞， ( )−∞ + ∞， 0x > ( )2( ) ( ) ( ) e 1 1xx k f x x x k x x′− < + ⇔ − − < + 1 0xe − > 1 1x xk xe +< +− 1( ) 1x xg x xe += +− min( )k g x< ( ) ( ) ( )2 2 e e 2e 1( ) 1 e 1 e 1 x xx x x xxg x − −− −′ = + = − − ( ) e 2xh x x= − − 则当 时， ， 在 上单调递增， 且 ， 故 在 上存在唯一零点， 设此零点为 ，则 ，即 ， 当 时， ，当 时， ， 于是 ， ∴ ，又 为整数， ∴ 的最大值为 . 【点睛】本题考查利用导数研究函数的单调性，考查不等式的恒成立问题，培养学生的逻辑 推理能力，运算求解能力，属于中档题． （二）选考题:共 10 分.考生在第 22,23 两题中任选一题做答,如果多做,则按所 做的第一题记分,答时用 2B 铅笔在答题卡上把目的题号涂黑. 22.在直角坐标系 中，直线 的参数方程为 （ 为参数），曲线 的参数方程 为 （ 为参数），以该直角坐标系的原点 为极点， 轴的非负半轴为极轴 建立极坐标系，曲线 的极坐标方程为 ． （1）分别求曲线 的极坐标方程和曲线 的直角坐标方程； （2）设直线 交曲线 于 ， 两点，交曲线 于 ， 两点，求 的长． 【 答 案 】（ Ⅰ ） 曲 线 的 极 坐 标 方 程 为 ： ； 的 直 角 坐 标 方 程 为 ： ；（Ⅱ） 【解析】 【分析】 （I）消去参数，即可得到曲线 的直角坐标方程，结合 ，即可 0x > ( ) e 1 0xh x′ = − > ( )h x ( )0，+ ∞ (1) 0 (2) 0h h< >， ( )h x ( )0，+ ∞ 0x ( ) 0 0 0 0(1,2) e 2 0xx h x x∈ = − − =， 0 0 2xe x= + ( )00x x∈ ， ( ) 0g x′ < ( )0x x∈ + ∞， ( ) 0g x′ > ( ) ( ) 0 0 min 0 0 0 1( ) 1 2 3e 1x xg x g x x x += = + = + ∈− ， 0 1k x< + k k 2 xOy l 3 3 x t y t = = − t 1C 2 2cos 2sin x y θ θ = +  = θ O x 2C 2 3 cos 2sinρ θ θ= − 1C 2C l 1C O A 2C O B | |AB 1C 4cosρ θ= 2C 2 2( 3) ( 1) 4x y− + + = 4 2 3− 2C 2 2 , cosx y xρ ρ θ= + = 得到曲线 的极坐标方程．（II）计算直线 l 的直角坐标方程和极坐标方程，计算 长， 即可． 【详解】解法一：（Ⅰ）曲线 ： （ 为参数）可化为直角坐标方程： ， 即 ， 可得 ， 所以曲线 的极坐标方程为： . 曲线 ： ，即 ， 则 的直角坐标方程为： . （Ⅱ）直线 的直角坐标方程为 ， 所以 的极坐标方程为 . 联立 ，得 ， 联立 ，得 ， . 解法二：（Ⅰ）同解法一 （Ⅱ）直线 直角坐标方程为 ， 联立 ，解得 ， 的 1C AB 1C 2 2 2 x cos y sin θ θ = +  = θ ( )2 22 4x y− + = 2 2 4 0x y x+ − = 2 4 cos 0ρ ρ θ− = 1C 4cosρ θ= 2C 2 3cos 2sinρ θ θ= − 2 2 3 cos 2 sinρ ρ θ ρ θ= − 2C ( ) ( )2 23 1 4x y− + + = l 3 3y x= − l ( )5 6 R πθ ρ= ∈ 5 6 4cos πθ ρ θ  =  = 2 3A ρ = − 5 6 2 3 2cos sin πθ ρ θ θ  =  = − 4B ρ = − 4 2 3A BAB ρ ρ= − = − l 3 3y x= − 2 2 3 3 4 0 y x x x y  = −  − + = ( )3, 3A − 联立 ，解得 ， 所以 . 【点睛】本小题考查直线和圆的极坐标方程、参数方程等基础知识，考查运算求解能力，考 查数形结合思想、化归与转化思想等. 23.已知 a>0,b>0,c>0,函数 f（x）=|a－x|+|x+b|+c. （1）当 a=b=c=2 时,求不等式 f（x）<10 的解集; （2）若函数 f（x）的最小值为 1,证明: . 【答案】（1） （2）证明见解析 【解析】 【分析】 （1）将 a＝b＝c＝2 代入，分类讨论即可求解； （2）利用基本不等式容易得证． 【详解】解：（1）当 时， 所以 或 或 所以不等式的解集为 （2）因为 所以 因为 的最小值为 ，所以 所以 因为 所以 所以 ( ) ( )2 2 3 3 3 1 4 y x x y  = −  − + + = ( )2 3, 2B − ( ) ( )2 2 2 3 3 2 3 4 2 3AB = − + − + = − 2 2 2 1 3a b c+ + ≥ { }| 4 4x x− < < 2a b c= = = ( ) | 2 | | 2 | 2f x x x= − + + + 2( ) 10 2 2 10 xf x x −< ⇔  − <  2 2 6 10 x− < <  < 2 2 2 10 x x   + <  { }| 4 4x x− < < 0 0 0a b c> > >， ， ( ) | | | | | | |f x a x x b c a x x b c a b c a b c= − + + + − + + + = + + = + + ( )f x 1 1a b c+ + = 2 2 2 2( ) 2 2 2 1a b c a b c ab ac bc+ + = + + + + + = 2 2 2 2 2 22 2 2ab a b bc b c ac a c+ + +≤ ， ≤ ， ≤ ( )2 2 2 2 2 21 2 2 2 3a b c ab ac bc a b c= + + + + + + +≤ 2 2 2 1 3a b c+ +  【点睛】本题考查绝对值不等式的解法及基本不等式的运用，考查推理论证能力，属于基础 题．