数学（文）卷·2019届湖南省长郡中学高二上学期期末考试（2018-01）

数学（文）卷·2019届湖南省长郡中学高二上学期期末考试（2018-01）

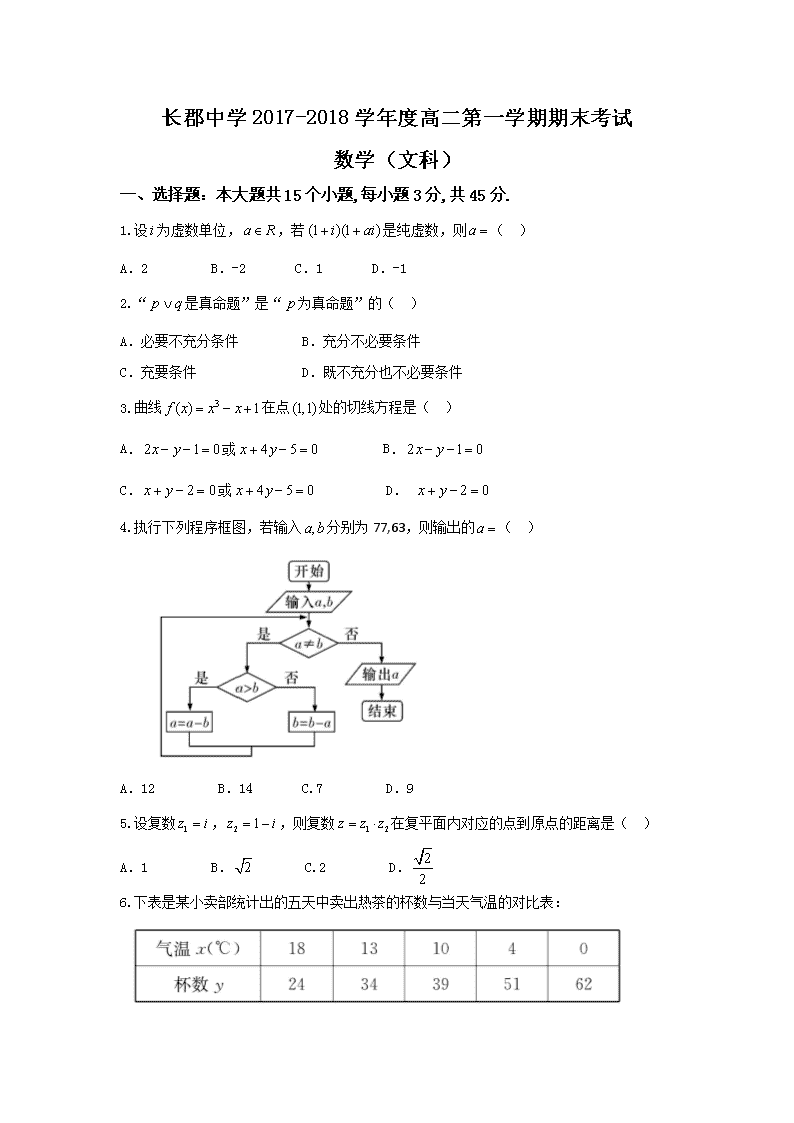
长郡中学2017-2018学年度高二第一学期期末考试 数学（文科）‎ 一、选择题：本大题共15个小题,每小题3分,共45分.‎ ‎1.设为虚数单位，，若是纯虚数，则（ ）‎ A．2 B．-2 C．1 D．-1‎ ‎2.“是真命题”是“为真命题”的（ ）‎ A．必要不充分条件 B．充分不必要条件 ‎ C．充要条件 D．既不充分也不必要条件 ‎3.曲线在点处的切线方程是（ ）‎ A．或 B． ‎ C．或 D． ‎ ‎4.执行下列程序框图，若输入分别为77,63，则输出的（ ）‎ A．12 B．14 C.7 D．9‎ ‎5.设复数，，则复数在复平面内对应的点到原点的距离是（ ）‎ A．1 B． C.2 D．‎ ‎6.下表是某小卖部统计出的五天中卖出热茶的杯数与当天气温的对比表：‎ 若卖出热茶的杯数与气温近似地满足线性关系，则其关系式最接近的是（ ）‎ A． B． ‎ C. D．‎ ‎7.若，，则一定有（ ）‎ A． B． C. D．‎ ‎8.极坐标方程和参数方程（为参数）所表示的图形分别是（ ）‎ A．直线、直线 B．圆、圆 ‎ C.直线、圆 D．圆、直线 ‎9.设是双曲线上一点，分别是双曲线左、右两个焦点，若，则等于（ ）‎ A．1 B．17 ‎ C.1或17 D．以上答案均不对 ‎10.某中学学生会为了调查爱好游泳运动与性别是否有关，通过随机询问110名性别不同的高中生是否爱好游泳运动得到如下的列联表：由并参照附表，得到的正确结论是（ ）‎ A．在犯错误的概率不超过的前提下，认为“爱好游泳运动与性别有关” ‎ B．在犯错误的概率不超过的前提下，认为“爱好游泳运动与性别无关” ‎ C.有的把握认为“爱好游泳运动与性别有关” ‎ D．有的把握认为“爱好游泳运动与性别无关”‎ ‎11.椭圆的左、右焦点分别为，是上的点，，，则的离心率为（ ）‎ A． B． C. D．‎ ‎12.若关于的不等式的解集为，则实数的取值范围是（ ）‎ A． B． ‎ C. D．‎ ‎13.一次试验：向如图所示的正方形中随机撒一大把豆子，经查数，落在正方形的豆子的总数为粒，其中有粒豆子落在该正方形的内切圆内，以此估计圆周率的值为（ ）‎ A． B． C. D．‎ ‎14.已知函数.若方程在内有实数解，则实数的最小值是（ ）‎ A． B． C. D．‎ ‎15.已知椭圆的离心率为，动是其内接三角形，且.若的中点为，的轨迹的离心率为，则（ ）‎ A． B． C. D．‎ 二、填空题：本大题共5小题，每小题3分，共20分.‎ ‎16.命题，，则 ．‎ ‎17.抛物线的焦点坐标是 ．‎ ‎18.已知，函数在上是单调函数，则的最大值是 ．‎ ‎19.某珠宝店丢了一件珍贵珠宝，以下四人中只有一人说真话，只有一人偷了珠宝.甲：我没有偷；乙：丙是小偷；丙：丁是小偷；丁：我没有偷.根据以上条件，可以判定偷珠宝的人是 ．‎ ‎20.已知，用数学归纳法证明时，等于 ．‎ 三、解答题：本大题共5小题，每小题8分，共40分，要求写出必要的文字说明、证明过程或演算步骤. ‎ ‎21.共享单车的推广给消费者带来全新消费体验，迅速赢得广大消费者的青睐，然而，同时也暴露出管理、停放、服务等方面的问题，为了了解公众对共享单车的态度（提倡或不提倡），某调查小组随机地对不同年龄段50人进行调查，将调查情况整理如下表：‎ 并且，年龄在和的人中持“提倡”态度的人数分别为5和3，现从这两个年龄段中随机抽取2人征求意见.‎ ‎（Ⅰ）求年龄在中被抽到的2人都持“提倡”态度的概率；‎ ‎（Ⅱ）求年龄在中被抽到的2人至少1人持“提倡”态度的概率.‎ ‎22.以平面直角坐标系的原点为极点，轴正半轴为极轴建立极坐标系，已知圆的极坐标方程为，直线的参数方程为（为参数），若与交于两点.‎ ‎（Ⅰ）求圆的直角坐标方程；‎ ‎（Ⅱ）设，求的值.‎ ‎23.证明：‎ ‎（Ⅰ）已知是正实数，且.求证：；‎ ‎（Ⅱ）已知，且，，.求证：中至少有一个是负数.‎ ‎24.已知椭圆的左、右两个焦点分别为，离心率，短轴长为2.点为坐标原点.‎ ‎（Ⅰ）求椭圆的方程；‎ ‎（Ⅱ）设点为椭圆上的一动点（非长轴端点），的延长线与椭圆交于点，的延长线与椭圆交于点，若的面积为，求直线的方程.‎ ‎25.已知函数.‎ ‎（Ⅰ）求函数的单调区间与极值；‎ ‎（Ⅱ）若，且，证明：.‎ 试卷答案 一、选择题 ‎1-5:CABCB 6-10:CCDBA 11-15：DADDA 二、填空题 ‎16. ， 17. 18.3 19.甲 ‎ ‎20. ‎ 三、解答题 ‎21.解：（Ⅰ）设在中的6人持“提倡”态度的为，持“不提倡”态度的为.总的基本事件有，，，，.共15个，其中两人都持“提倡”态度的有10个，所以 ‎（Ⅱ）设在中的5人持“提倡”态度的为，持“不提倡”态度的为.总的基本事件有，，，，，共10个，其中两人都持“不提倡”态度的只有一种，所以 ‎22.解：（Ⅰ）由，得，‎ ‎（Ⅱ）把，‎ 代入上式得，‎ ‎∴，则，，‎ ‎.‎ ‎23.解：（Ⅰ）因为均为正数，欲证，只要证明，也即证，也即证明，这与已知条件相符，且以上每个步骤都可逆，故不等式成立.‎ ‎（Ⅱ）假设都是非负数，因，‎ 故，又，‎ 故，与题设矛盾，故假设不成立，原命题成立.‎ ‎24.解：（Ⅰ）由题意得，∴，‎ ‎∵，，∴，，‎ ‎∴椭圆的方程为.‎ ‎（Ⅱ）①当直线斜率不存在时，不妨取、、，‎ ‎∴面积为，不符合题意.‎ ‎②当直线斜率存在时，设直线，‎ 由，化简得，‎ 设，，，，‎ ‎∴‎ ‎，‎ ‎∵点的直线的距离，‎ 又是线段的中点，∴点到直线的距离为，‎ ‎∴面积为 ‎，‎ ‎∴，∴，‎ ‎∴，∴，或，‎ ‎∴直线的方程为或.‎ ‎25.解：（Ⅰ）由，‎ 易得的单调增区间为，单调减区间为，‎ 函数在处取得极大值，且 ‎（Ⅱ）由，，不妨设，则必有，‎ 构造函数，，‎ 则，所以在上单调递增，，也即对恒成立.‎ 由，则，‎ 所以，‎ 即，又因为，，且在上单调递减，‎ 所以，即证.‎