山西省2018-2019学年高一上学期期末测评考试 数学（I）

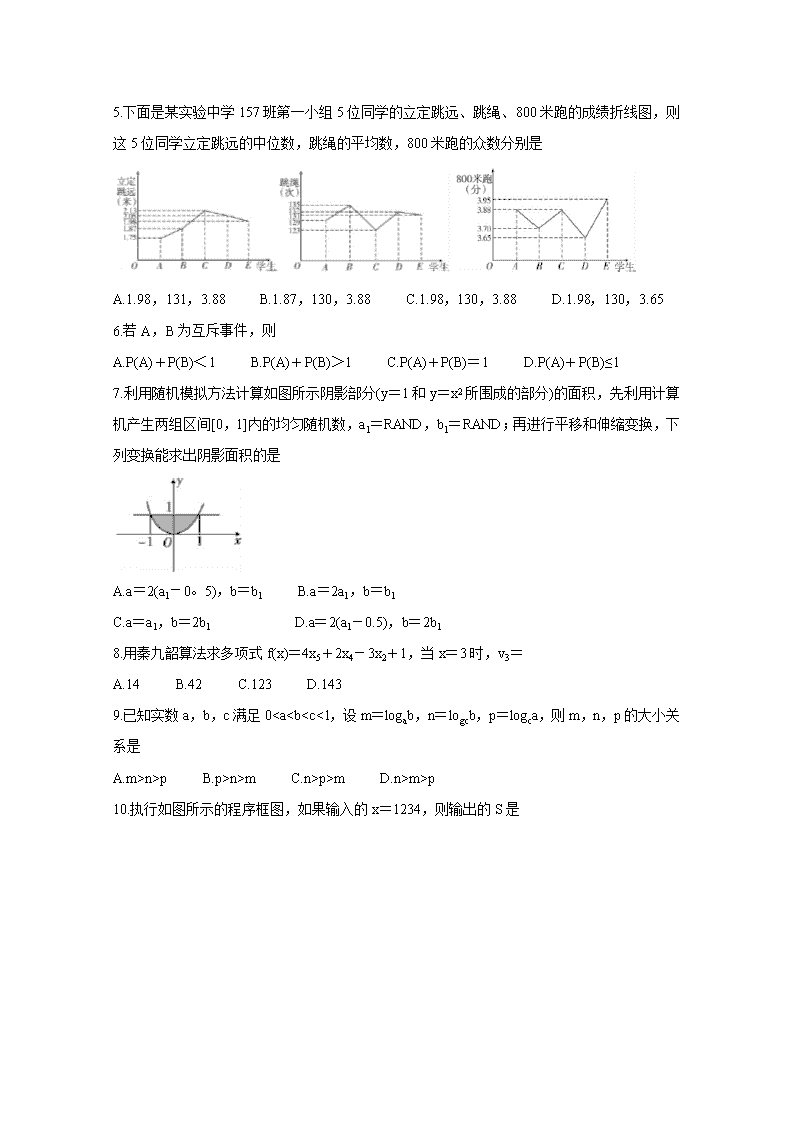
山西省2018-2019学年高一上学期期末测评考试 数学（I）

www.ks5u.com 秘密★启用前 高一数学(I)试题 注意事项：‎ ‎1.答卷前，考生务必将自己的姓名、准考证号填写在本试题相应的位置。‎ ‎2.全部答案在答题卡上完成，答在本试题上无效。‎ ‎3.回答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案用0。5mm黑色笔迹签字笔写在答题卡上。‎ ‎4.考试结束后，将本试题和答题卡一并交回。‎ 一、选择题：本题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎1.若集合A＝{x|x>－1}，B＝{－2，－1，1，2}，则A∩B＝‎ A.{－1，1，2} B.{1，2} C.{x|x＞－1} D.{－2，－1}∪(－1，＋∞)‎ ‎2.如图，正方形ABCD的边长为2，以正方形的每个顶点为圆心，1为半径作圆，在正方形内随机取一点，则此点取自阴影部分的概率是 A. B.1－ C. D.‎ ‎3.下列两个变量具有正相关关系的是 A.正方形的面积与边长 B.吸烟与健康 C.数学成绩与物理成绩 D.汽车的重量与汽车每消耗1L汽油所行驶的平均路程 ‎4.执行右边的程序，若输入n＝3，则输出S＝‎ A.4 B.6 C.8 D.10‎ ‎5.下面是某实验中学157班第一小组5位同学的立定跳远、跳绳、800米跑的成绩折线图，则这5位同学立定跳远的中位数，跳绳的平均数，800米跑的众数分别是 A.1.98，131，3.88 B.1.87，130，3.88 C.1.98，130，3.88 D.1.98，130，3.65‎ ‎6.若A，B为互斥事件，则 A.P(A)＋P(B)＜1 B.P(A)＋P(B)＞1 C.P(A)＋P(B)＝1 D.P(A)＋P(B)≤1‎ ‎7.利用随机模拟方法计算如图所示阴影部分(y＝1和y＝x2所围成的部分)的面积，先利用计算机产生两组区间[0，1]内的均匀随机数，a1＝RAND，b1＝RAND；再进行平移和伸缩变换，下列变换能求出阴影面积的是 A.a＝2(a1－0。5)，b＝b1 B.a＝2a1，b＝b1‎ C.a＝a1，b＝2b1 D.a＝2(a1－0.5)，b＝2b1‎ ‎8.用秦九韶算法求多项式f(x)＝4x5＋2x4－3x2＋1，当x＝3时，v3＝‎ A.14 B.42 C.123 D.143‎ ‎9.已知实数a，b，c满足0n>p B.p>n>m C.n>p>m D.n>m>p ‎10.执行如图所示的程序框图，如果输入的x＝1234，则输出的S是 A.14 B.15 C.16 D.17‎ ‎11.右图是甲、乙两人六次综合测评成绩的茎叶图，其中一个数字被污损，已知x∈N且x＜10，若甲、乙两人的平均数相同，则甲的方差是 A.23 B. C.25 D.5‎ ‎12.已知函数f(x)是定义在(－∞，0)∪(0，＋∞)上的偶函数，当x＞0时，‎ ‎，若方程，[f(x)]2＋af(x)＋b＝0有且只有6个不同实数根，则实数a的取值范围是 A.(4，＋∞) B.[4，＋∞) C.(－∞，－4] D.(－∞，－4)‎ 二、填空题：本题共4小题，每小题5分，共20分。‎ ‎13.72和168的最大公约数是 。‎ ‎14.小明将本班的51个同学编号为01，02，03，…，51，并依次将其平分为17个小组，组号为1，2，…，17，现用系统抽样法抽取一个容量为17的样本，若样本中有一个同学的编号为46，则组号为6的小组中抽到的号码为 。‎ ‎15.记函数的定义域为D，在区间[－3，5]上随机取一个数x，则x∈D的概率为 。‎ ‎16.已知函数f(x)＝log2(4x)·log4(2x)，x∈[，8]，则f(x)的最小值为 。‎ 三、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。‎ ‎17.(10分)‎ 某函数的解析式由如图所示的程序框图给出。‎ ‎(1)写出该函数的解析式；‎ ‎(2)执行该程序框图，若输出的结果为4，求输入的实数x的值。‎ ‎18.(12分)‎ 已知一个口袋有3个白球，1个黑球，这些球除颜色外全部相同，现将口袋中的球随机逐个取出，并依次放入编号为1，2，3，4的抽屉内。‎ ‎(1)求编号为2的抽屉内放黑球的概率；‎ ‎(2)口袋中的球放入抽屉后，随机取出两个抽屉中的球，求取出的两个球是一黑一白的概率。‎ ‎19.(12分)‎ 某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x(单位：万元)对年销售量y(单位：t)的影响，对近4年的年宣传费xi和年销售量yi(i＝1，2，3，4)作了初步统计和处理，得到的数据如下：‎ ‎。‎ ‎(1)在给定的坐标系中画出表中数据的散点图；‎ ‎(2)求出y关于x的线性回归方程；‎ ‎(3)若公司计划下一年度投入宣传费6万元，试预测年销售量y的值。‎ 参考公式 ‎20.(12分)‎ 随着手机的普及，大学生迷恋手机的现象非常严重。为了调查双休日大学生使用手机的时间，某机构采用不记名方式随机调查了使用手机时间不超过10小时的50名大学生，将50人使用手机的时间分成5组：(0，2］，(2，4］，(4，6］，(6，8］，(8，10］分别加以统计，得到下表，根据数据完成下列问题：‎ ‎(1)完成频率分布直方图，并根据频率分布直方图估计大学生使用手机时间的中位数(保留小数点后两位)；‎ ‎(2)用分层抽样的方法从使用手机时间在区间(0，2］，(2，4］，(4，6］的大学生中抽取6人，再从这6人中随机抽取2人，求这2人取自不同使用时间区间的概率。‎ ‎21.(12分)‎ 已知函数f(x)＝lg(x＋)。‎ ‎(1)判断函数f(x)的奇偶性；‎ ‎(2)若f(1－m)＋f(2m＋1)≤0，求实数m的取值范围。‎ ‎22.(12分)‎ 已知函数F(x)＝f(x)－g(x)。‎ ‎(1)若函数f(x)＝x，g(x)＝x2＋2x－2，求函数F(x)的零点；‎ ‎(2)若函数f(x)＝ax2－1，g(x)＝lnx，函数F(x)在区间[，1]上有且仅有两个零点x0和ex0，求实数a的取值范围。‎ ‎ ‎ ‎ ‎ ‎ ‎