数学文卷·2018届福建省漳州市芗城中学高二上学期期末考试（2017-01）无答案

数学文卷·2018届福建省漳州市芗城中学高二上学期期末考试（2017-01）无答案

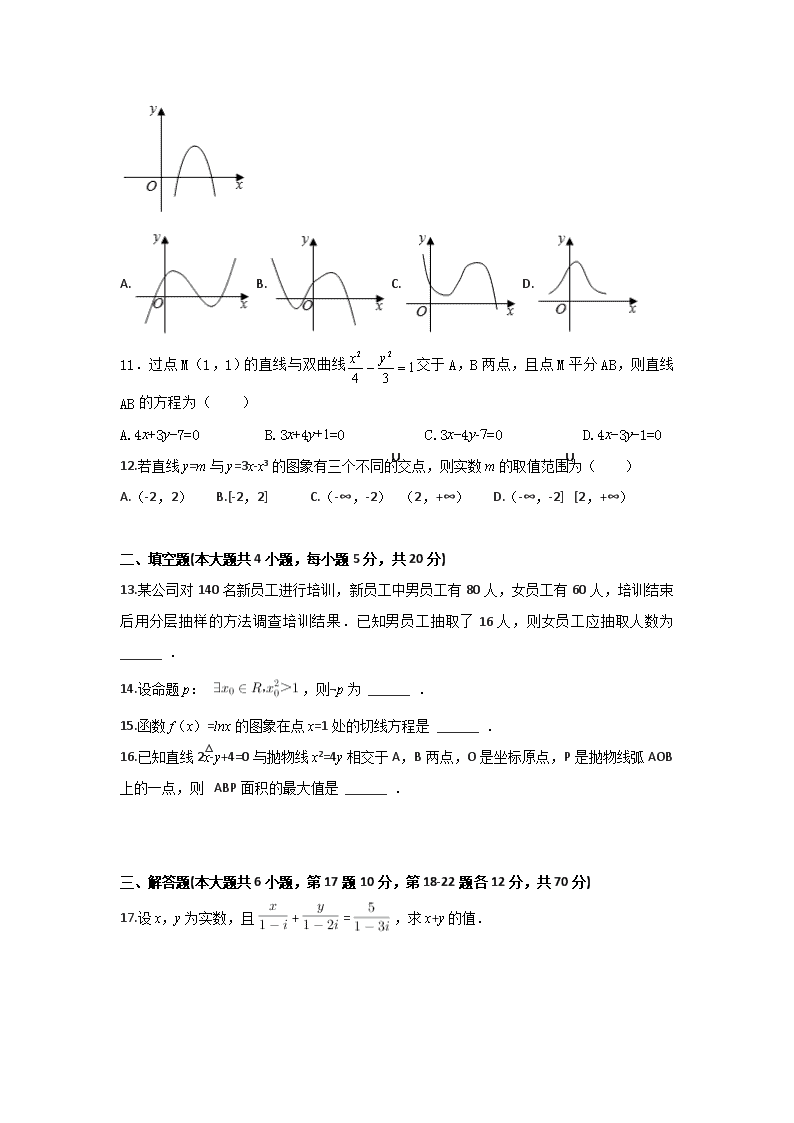
‎ 2016-2017学年高二上学期文科数学期末试卷 命题人：谢雪晶 ‎ 一、选择题(本大题共12小题，每小题5分，共60分)‎ ‎1.若复数（a+i）（1+2i）是纯虚数（i是虚数单位，a是实数），则a等于（　　） A.       B.2        C.-       D.-2‎ x=4‎ y=2‎ x=x/y y=4*x+1‎ PRINT x+y END ‎2.已知某物体的运动方程是s=+t，则当t=3s时的瞬时速度是（　　） A.2m/s      B.3m/s      C.4m/s      D.5m/s ‎3.运行如图程序，则输出的结果是（　　） A.9        B.11       C.17       D.19‎ ‎4.“x=1”是“x2-2x+1=0”的 （　　） ‎ A.充分不必要条件             B.必要不充分条件 ‎ C.充要条件                D.既不充分也不必要条件 ‎5.从装有3个红球、2个白球的袋中任取2个球，则所取的2个球中至少有1个白球的概率是（　　） A.  B.  C.  D.‎ ‎6. 为了解1500名学生对学校教改试验的意见，打算从中抽取一个容量为50的样本，考虑采用系统抽样，则分段的间隔k为（　　） A.40     B.20     C.30     D.12‎ ‎7.已知△ABC的顶点B、C在椭圆+y2=1上，顶点A是椭圆的一个焦点，且椭圆的另外一个焦点在BC边上，则△ABC的周长是（　　） A.2      B.4       C.6       D.12‎ ‎8.执行如图所示的程序框图，则输出的k的值是（　　） A.3        B.4        C.5        D.6‎ ‎9.点P为△ABC边AB上任一点，则使S△PBC≤S△ABC的概率是（　　） A.  B.  C.  D.‎ ‎10.若函数y=f（x）的导函数y=f′（x）的图象如图所示，则y=f（x）的图象可能（　　） ‎ ‎ A. B. C. D.‎ ‎11．过点M（1，1）的直线与双曲线交于A，B两点，且点M平分AB，则直线AB的方程为（　　） A.4x+3y-7=0   B.3x+4y+1=0   C.3x-4y-7=0   D.4x-3y-1=0‎ ‎12.若直线y=m与y=3x-x3的图象有三个不同的交点，则实数m的取值范围为（　　） A.（-2，2）  B.[-2，2] C.（-∞，-2）∪（2，+∞）   D.（-∞，-2]∪[2，+∞）‎ 二、填空题(本大题共4小题，每小题5分，共20分)‎ ‎13.某公司对140名新员工进行培训，新员工中男员工有80人，女员工有60人，培训结束后用分层抽样的方法调查培训结果．已知男员工抽取了16人，则女员工应抽取人数为 ______ ．‎ ‎14.设命题p： ，则¬p为 ______ ．‎ ‎15.函数f（x）=lnx的图象在点x=1处的切线方程是 ______ ．‎ ‎16.已知直线2x-y+4=0与抛物线x2=4y相交于A，B两点，O是坐标原点，P是抛物线弧AOB上的一点，则△ABP面积的最大值是 ______ ．‎ 三、解答题(本大题共6小题，第17题10分，第18-22题各12分，共70分)‎ ‎17.设x，y为实数，且+=，求x+y的值． ‎ ‎18.设p：实数x满足x2-4ax+3a2＜0，其中a＞0；q：实数x满足＜0． （1）若a=1，且p∧q为真，求实数x的取值范围； （2）若p是q的必要不充分条件，求实数a的取值范围． ‎ ‎19.某校高中一年级组织学生参加了环保知识竞赛，并抽取了其中20名学生的成绩进行分析．右图是这20名学生竞赛成绩（单位：分）的频率分布直方图，其分组为[100，110），[110，120），…，[130，140），[140，150]． （Ⅰ）求图中a的值及成绩分别落在[100，110）与[110，120）中的学生人数； （Ⅱ） 学校决定从成绩在[110，120）的学生中任选2名进行座谈，求这2人的成绩都在[110，120）的概率． ‎ ‎ 20.为了解某地区观众对大型综艺活动《中国好声音》的收视情况，随机抽取了100名 观众进行调查，其中女性有55名．下面是根据调查结果绘制的观众收看该节目的场数与所对应的人数表： ‎ 场数 ‎9‎ ‎10‎ ‎11‎ ‎12‎ ‎13‎ ‎14‎ 人数 ‎10‎ ‎18‎ ‎22‎ ‎25‎ ‎20‎ ‎5‎ 将收看该节目场次不低于13场的观众称为“歌迷”，已知“歌迷”中有10名女性． （Ⅰ）根据已知条件完成下面的2×2列联表，并据此资料我们能否有95%的把握认为“歌迷”与性别有关？ ‎ 非歌迷 歌迷 合计 男 女 合计 ‎（Ⅱ）将收看该节目所有场次（14场）的观众称为“超级歌迷”，已知“超级歌迷”中有2名女性，若从“超级歌迷”中任意选取2人，求至少有1名女性观众的概率． ‎ P（K2≥k）‎ ‎0.05‎ ‎0.01‎ k ‎3.841‎ ‎6.635‎ 附：K2=． 21.已知椭圆的焦点为F1、F2，抛物线y2=px（p＞0）与椭圆在第一象限的交点为Q，若∠F1QF2=60°． （1）求△F1QF2的面积； （2）求此抛物线的方程． ‎ ‎22.已知函数f(x)=x3-(a∈R)． (Ⅰ)若a=1，求函数f(x)在[0，2]上的最大值； (Ⅱ)若对任意x∈(0，+∞)，有f(x)＞0恒成立，求a的取值范围． ‎ ‎ ‎